Основные этапы развития параллельной обработки

Идея параллельной обработки возникла одновременно с появлением первых вычислительных машин. В начале 50-х гг. американский математик Дж. Фон Нейман предложил архитектуру последовательной ЭВМ, которая приобрела классические формы и применяется практически во всех современных ЭВМ. Однако фон Нейман разработал также принцип построения процессорной матрицы, в которой каждый процессор был соединен с четырьмя соседними.

D825. Одной из первых полномасштабных многопроцессорных систем явилась система D825 фирмы “BURROUGHS”. Начиная с 1962 г. было выпущено большое число экземпляров и модификаций D825. Выпуск первых многопроцессорных систем, в частности D825, диктовался необходимостью получения не высокого быстродействия, а высокой живучести ЭВМ, встраиваемых в военные командные системы и системы управления. С этой точки зрения параллельные ЭВМ считались наиболее перспективными. Система D825 содержала до четырех процессоров и 16 модулей памяти, соединенных матричным коммутатором, который допускал одновременное соединение любого процессора с любым блоком памяти.

Практическая реализация основных идей параллельной обработки началась только в 60-х гг. 20 - го столетия. Это связано с появлением транзистора, который позволил строить машины, состоящие из большого количества логических элементов, что принципиально необходимо для реализации любой формы параллелизма.

CRAY. Основополагающим моментом для развития конвейерных ЭВМ явилось обоснование академиком С.А. Лебедевым в 1956 г. метода, названного

“принципом водопровода” (позже он стал называться конвейером). Прежде все-

го был реализован конвейер команд, на основании которого практически одно-

временно были построены советская ЭВМ БЭСМ-6 (1957-1966 гг., разработка

Института точной механики и вычислительной техники АН СССР), и англий-

ская машина ATLAS (1957-1963 гг.). Конвейер команд предполагал наличие

многоблочной памяти и секционированного процессора, в котором на разных

этапах обработки находилось несколько команд.

Следующим заметным шагом в развитии конвейерной обработки, реализо

ванном в ЭВМ CDC-6600 (1964 г.), было введение в состав процессора не-

скольких функциональных устройств, позволяющих одновременно выполнять

несколько арифметико-логических операций: сложение, умножение, логические операции.

В конце 60-х гг. был введен в использование арифметический конвейер, который нашел наиболее полное воплощение в ЭВМ CRAY-1 (1972-1976 гг.).

Арифметический конвейер предполагает разбиение цикла выполнения арифме-

тико-логической операции на ряд этапов, для каждого из которых отводится

собственное оборудование. Таким образом, на разных этапах обработки нахо-

дится несколько чисел, что позволяет производить эффективную обработку

вектора чисел.

Сочетание многофункциональности, арифметического конвейера для каж

дого функционального блока и малой длительности такта синхронизации по-

зволяет получить быстродействие в десятки и сотни миллионов операций в се-

кунду. Такие ЭВМ называются супер ЭВМ.

ILLIAC-IV. Идея получения сверхвысокого быстродействия в первую очередь связывалась с процессорными матрицами (ПМ). Предполагалось, что,

увеличивая в нужной степени число процессорных элементов в матрице, можно

получить любое заранее заданное быстродействие.

Поскольку в 60-е гг. логические схемы с большим уровнем интеграции от

сутствовали, то напрямую реализовать принципы функционирования процес-

сорной матрицы, содержащей множество элементарных процессоров, не пред-

ставлялось возможным. Поэтому для проверки основных идей строились одно-

родные системы из нескольких больших машин. Так, в 1966 г. была построена

система Минск-222, разработанная Институтом математики Сибирского отде-

ления АН СССР и минским заводом ЭВМ им. Г.К.Орджоникидзе. Система со-

держала до 16 соединенных в кольцо ЭВМ Минск-2. Для нее было разработано

специальное математическое обеспечение.

Другое направление в развитии однородных сред, основанное на построе-

нии процессорных матриц, состоящих из крупных процессорных элементов с

достаточно большой локальной памятью, возникло в США и связано с именами

Унгера, Холланда, Слотника. Была создана ЭВМ ILLIAC-IV (1966-1975 гг.), ко-

торая надолго определила пути развития процессорных матриц. В машине ис-

пользовались матрицы 8×8 процессоров, каждый с быстродействием около 4

млн оп/с и памятью 16 кбайт. Для ILLIAC-IV были разработаны кроме Ассемб-

лера еще несколько параллельных языков высокого уровня. Особенно ценным

является опыт разработки параллельных алгоритмов вычислений, определив-

ший области эффективного использования подобных машин.

Tранспьютер. Совершенствование микроэлектронной элементной базы,

появление в 80-х годах БИС и СБИС позволили разместить в одной микросхеме

процессор с 4-мя внешними связями, который получил название транспьютер.

Теперь стало возможным строить системы с сотнями процессоров.

Вычислительные кластеры. Далее развитие и производство супер-ЭВМ

пошло широким потоком. Сначала строились монолитные многопроцессорные

системы, для которых все разрабатывалось специально для конкретной систе-

мы: элементная база, конструктивы, языки программирования, операционные

системы. Затем оказалось много дешевле строить вычислительные кластеры на

основе промышленные средства, появились многояденые процессора, Грид,

квантовые компьютеры.

Некоторые этапы развития параллельных ЭВМ качественно можно представить следующей таблицей:

 

№	НАЗВАНИЕ ЭВМ	ГОДЫ	НОВИЗНА	ПРОГРАММЫ
	D825 - одна из первых многопроцессорных систем		Доказана возможность построения многопроцессорных систем	Первая ОС для многопроцессорных систем - ASOR
	Матричный процессор ILLIAC IV		Реализована ОКМД машина	Параллельный язык Glupnir
	Векторно- конвейерная ЭВМ CRAY		Предложены конвейерные вычисления	Предложен ЯВУ векторного типа
	Транспьютер Т414		Разработан процессор на кристалле со связями для мультисистем	Язык описания параллелизма OCCAM
	Кластер Beowulf		Сборка на серийном оборудовании	Использованы обыч ные сетевые ОС
	Грид		Неограниченная возможность расширения	GlobusToolkit, gLite
	Многоядерные про- цессоры		Разработаны МЯ процессоры с общей и индивидуальной памятью	OpenMP и MPI. Нужны новые разработки
	Квантовый компью- тер Orion компании D-Wave		Кубит, эспоненциальная скорость за счет суперпозиции	Алгоритмы Шора, Гровера. Языки моделирования

 

ЛЕКЦИЯ 5.

МЕЛКОЗЕРНИСТЫЙ ПАРАЛЛЕЛИЗМ

Мелкозернистый параллелизм обеспечивается за счет параллелизма внутри базовых блоков (ББ), которые являются частями программ, не содержащими

условных и безусловных переходов. Этот вид параллелизма реализуется блока-

ми одного процессора: различными АЛУ, умножителями, блоками обращения к

памяти, хранения адреса, переходов и так далее.

 

Принципы распараллеливания и планирования базовых блоков.

Размер ББ и его увеличение. Базовые блоки невелики по размеру (5 − 20

команд) и даже при оптимальном планировании параллелизм не может быть

большим. На рисунке точками представлена экспериментальная зависимость

ускорения от размера базового блока. Поле полученных в экспериментах ре-

зультатов ограничено контуром (точками представлены значения для некото-

рых ББi).

	r

w

 

На основе рисунка с учетом вероятностных характеристик контура ре-

зультатов можно получить следующую качественную зависимость:

h = a + b w,

 

где a и b — константы (a ≈ 1, b ≈ 0,15), h - средняя ширина параллелизма (чис-

ло параллельных ветвей), w – число команд в программе. Следовательно,

можно сказать, что

Здесь: tпар и tпосл – времена параллельного и последовательного исполнения одного и того же отрезка программы.

Таким образом, основной путь увеличения скалярного параллелизма про-

граммы − это удлинение ББ, а развертка − наиболее простой способ для этого.

Цикл:

DO 1 I=1,N

C(I) = A(I) + B(I)

1 CONTINUE

имеет небольшую длину ББ, но ее можно увеличить путем развертки приведен-

ного цикла на две, четыре и так далее итераций, как показано ниже

DO 1 I=1,N,2

C(I) = A(I) + B(I)

C(I+1) = A(I+1) + B(I+1)

1 CONTINUE

DO 1 I=1,N,4

C(I) = A(I) + B(I)

C(I+1) = A(I+1) + B(I+1)

C(I+2) = A(I+2) + B(I+2)

C(I+3) = A(I+3) + B(I+3)

1 CONTINUE

К сожалению, развертка возможна только, если:

• все итерации можно выполнять параллельно;

• в теле цикла нет условных переходов.

 

Метод Фишера. Существует большое количество методов увеличения па

раллелизма при обработке базовых блоков. Но в большинстве случаев тело

цикла содержит операторы переходов. Достаточно универсальный метод пла-

нирования трасс с учетом переходов предложил в 80-е годы J.Fisher. Рас-

смотрим этот метод на примере рисуна. На схеме в кружках представлены но-

мера вершин, а рядом − вес вершины (время ее исполнения); на выходах опера-

торов переходов проставлены вероятности этих переходов.

Возможны три варианта путей исполнения тела цикла:

• путь 1-2-4 обладает объемом вычислений (5+5+5) и вероятностью

0.8*0.8=0.64;

• путь 1-2 имеет объем вычислений 5+5 и вероятность 0.8*0.2=0.16;

• путь 1-3 имеет объем вычислений 5+1 и вероятность 0.2.

Примем путь 1-2-4 в качестве главной трассы. Остальные пути будем считать простыми трассами. Ограничимся рассмотрением метода планирования трасс только по отношению к главной трассе.

Если метод планирования трасс не применяется, то главная трасса состоит из трех независимых блоков. Суммарное время выполнения этих блоков будет в соответствии с вышеприведенными формулами равным:

В методе планирования трасс предлагается считать главную трассу единым ББ, который выполняется с вероятностью 0,64. Если переходов из данной трассы в другие трассы нет, то объединенный ББ выполняется за время

 

Таким образом, выигрыш во времени выполнения главной трассы составил Т1/Т2 = 1.8 раз. В общем случае при объединении k блоков с равным временем исполнения w получаем:

При построении ЯПФ объединенного ББ и дальнейшем планировании команды могут перемещаться из одного исходного ББ в другой, оказываясь выше или ниже оператора перехода, что может привести к нарушению логики выполнения программы.

Чтобы исключить возможность неправильных вычислений, вводятся ком-

пенсационные коды. Рассмотрим примеры рисунок. Пусть текущая трасса

(рис.а) состоит из операций 1, 2, 3. Предположим, что операция 1 не являет-

ся срочной и перемещается поэтому ниже условного перехода 2. Но тогда опе-

рация 4 читает неверное значение a. Чтобы этого не произошло, компилятор

вводит компенсирующую операцию 1 (рис.б).

Пусть теперь операция 3 перемещается выше оператора IF. Тогда операция 5 считает неверное значение d. Если бы значение d не использовалось на расположенном вне трассы крае перехода, то перемещение операции 3 выше оператора IF было бы допустимым.

г)

 

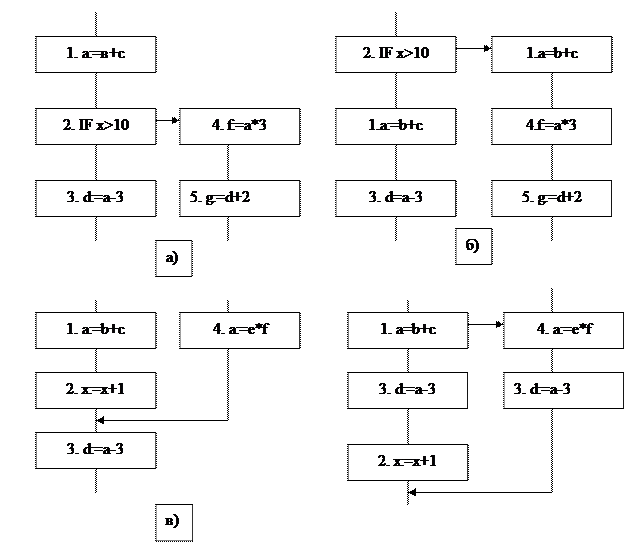
Рассмотрим переходы в трассу извне. Пусть текущая трасса содержит операции 1, 2, 3 (рис.в). Предположим, что компилятор перемещает операцию 3

в положение между операциями 1 и 2. Тогда в операции 3 будет использовано

неверное значение a. Во избежание этого, необходимо ввести компенсирующий

код 3 (рис.г).

Порядок планирования трасс для получения конечного результата таков:

1. Выбор очередной трассы и ее планирование (распараллеливание и размещение по процессорам).

2. Коррекция межтрассовых связей по результатам упаковки по процессорам очередной трассы. Компенсационные коды увеличивают размер машинной программы, но не увеличивают числа выполняемых в процессе вычислений

операций.

3. Если все трассы исчерпаны или оставшиеся трассы имеют очень низкую вероятность исполнения, то компиляция программы считается законченной, в противном случае осуществляется переход на пункт 1.

Основным объектом распараллеливания в области скалярного параллелизма являются базавые блоки. Если ББ представлен на язык высокого уровня, тогда распараллеливанию подвергаются арифметические выражения. Если ББ

представлен на ассемблер или в машинных кодах, то распараллеливается отре-

зок программы. Эти операции отличаются. Далее будут рассмотрены оба под-

хода, которые используются в компиляторах для автоматического распараллливания.

 

 

ЛЕКЦИЯ 6.