
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет зубьев конической передачи на выносливость по напряжениям изгиба.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Как известно, при работе зубья испытывают сложнонапряженное состояние, при этом наибольшие напряжения возникают у корня зуба в месте перехода эвольвентного профиля в галтель. В этом же месте возникает и концентрация напряжений. При расчете можно принять следующие допущения: 1. Вся нагрузка в зацеплении воспринимается одним зубом и приложена к его вершине. 2. Зуб рассматривается как консольная балка, для расчета которой справедливы методы сопротивления материалов. 3.4.1 Расчет в этом случае рекомендуется начинать с определения удельной расчетной окружной силы:
где: зубьями, его принимают равным
нагрузки по ширине зуба, его принимают равным
нагрузку равный,
3.4.2 Определение удельной окружной динамической силы:
3.4.3. Расчет напряжения при изгибе. Напряжение изгиба в зубе конической передачи вычисляется по формуле:
где: среднем нормальном сечении (рис. 5.17 [1]);
зубьев. Рассчитывается по формуле:
Условие изгибной прочности зубьев конической передачи
где:
(
приложения нагрузки (
концентрации напряжений и зависящий от m модуля (таб.5.8 [1]) (
поверхности, при шлифовании и зубофрезеровании;
Результаты расчетов свести в таблицу. 3.5. Контрольные вопросы. 1. В чем заключается метод эквивалентного зацепления при расчете конической передачи? 2. Является ли модуль зацепления в коническом колесе однозначным? 3. Какой параметр в коническом зацеплении является аналогом межосевого расстояния обычного прямозубого зацепления? 4. Какие силы учитываются в расчете конического колеса на контактную выносливость? 5. В чем заключается расчет прочности на изгиб зуба? 6. Каковы приемлемые диапазоны модулей для конических зацеплений? 7. Что такое удельная динамическая сила? 8. Что такое удельная нагрузка? 9. Какое напряжение учитывается при расчете прочности зуба на изгиб? 10. Какое напряжение учитывается при определении контактной выносливости?
4. РАСЧЕТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ.
Лабораторная работа №4 Цель работы: Освоить проектный расчет червячной передачи. Задачиработы: 1. Провести кинематический расчет червячной передачи. 2. Выполнить расчеты на прочность червячного колеса. 3. Определить условие самоторможения. 4. Выполнить эскиз червячного зацепления. Общие сведения. Геометрические расчеты аналогичны расчетам зубчатых передач, так как червяк является подобием косозубого эвольвентного колеса, у которого число зубьев равно числу витков резьбы. По числу винтовых линий резьбы червяк может быть однозаходным и многозаходным. С увеличением числа заходов возрастает угол подъема винтовой линии и повышается КПДпередачи. Однозаходные червяки применяют, когда необходимы большие передаточные числа или самоторможение. Червяки имеют обычно правую нарезку, кроме случаев, обусловленных требованиями кинематики. В зависимости от положения червяка относительно червячного колеса передачи бывают с верхним и нижним расположением червяка. При нижнем расположении условия для смазки лучше. Основные геометрические параметры червячной передачи: модуль Угол подъема винтовой линии определяют из соотношения
В цилиндрических передачах с архимедовым червяком шаг червяка Р и шаг зубьев червячного колеса совпадают. Геометрические размеры червяка и червячного колеса (рис. 4.1.) приведены в табл.4.1. ( В целях ограничения номенклатуры стандартного инструмента для нарезания червячных колес и червяков значения т, q, т, мм 1,0; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; q 6,3: 8; 10 (кроме т = 2); 12,5 (кроме т = 2,5); 16; 20;
Таблица 4.1.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

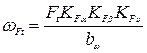 ,
,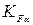 – коэффициент, учитывающий распределения нагрузки между
– коэффициент, учитывающий распределения нагрузки между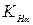 .
.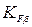 – коэффициент, учитывающий неравномерность распределения
– коэффициент, учитывающий неравномерность распределения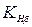 .
.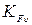 – коэффициент, учитывающий дополнительную динамическую
– коэффициент, учитывающий дополнительную динамическую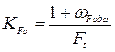 .
.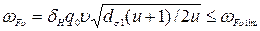
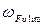 – зависит от степени точности (таб.5.5 [1]), 7 степень точности соответствует
– зависит от степени точности (таб.5.5 [1]), 7 степень точности соответствует 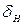 = 0,006 – для круговых зубьев;
= 0,006 – для круговых зубьев;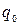 = 47 – для 7 степени точности;
= 47 – для 7 степени точности;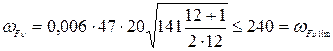 .
.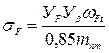 ,
,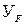 – коэффициент формы профиля конических зубьев, определяемый в
– коэффициент формы профиля конических зубьев, определяемый в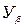 – коэффициент, учитывающий наклон линии зуба, для круговых
– коэффициент, учитывающий наклон линии зуба, для круговых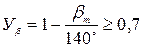 .
.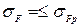
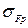 – допускаемое напряжение изгиба:
– допускаемое напряжение изгиба: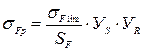 ,
,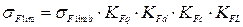 – предел напряжения при изгибе;
– предел напряжения при изгибе;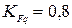 – шлифованные зубья;
– шлифованные зубья;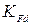 – коэффициент, учитывающий деформационное упрочнение
– коэффициент, учитывающий деформационное упрочнение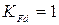 – деформационное упрочнение отсутствует);
– деформационное упрочнение отсутствует);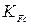 – коэффициент снижения
– коэффициент снижения 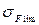 в случае двухстороннего
в случае двухстороннего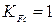 – односторонняя нагрузка);
– односторонняя нагрузка);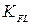 – коэффициент долговечности принимать равным 0,5;
– коэффициент долговечности принимать равным 0,5;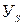 – коэффициент, учитывающий чувствительность материала к
– коэффициент, учитывающий чувствительность материала к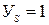 при m = 3);
при m = 3);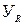 – коэффициент, учитывающий шероховатость переходной
– коэффициент, учитывающий шероховатость переходной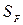 – коэффициент безопасности принимать 1,8.
– коэффициент безопасности принимать 1,8.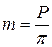 ;коэффициент диаметра червяка q; шаг резьбы червяка в осевом сечении P. Делительный диаметр червяка d
;коэффициент диаметра червяка q; шаг резьбы червяка в осевом сечении P. Делительный диаметр червяка d 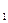 связан с модулем т коэффициентом диаметра червяка:
связан с модулем т коэффициентом диаметра червяка: 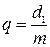 . Для многозаходных червяков ход
. Для многозаходных червяков ход 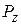 связан с шагом Р соотношением:
связан с шагом Р соотношением: 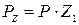 ,где
,где 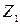 – число витков (заходов) червяка.
– число витков (заходов) червяка.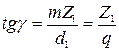 .
.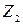 – число зубьев колеса).
– число зубьев колеса).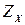 стандартизированы. Рекомендации по выбору т, q, Z приведены ниже (угол профиля в осевом сечении также стандартизирован: α = 20 °):
стандартизированы. Рекомендации по выбору т, q, Z приведены ниже (угол профиля в осевом сечении также стандартизирован: α = 20 °):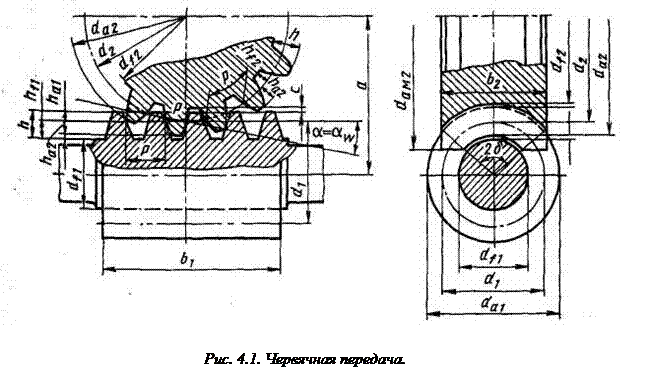
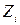 1; 2; 4.
1; 2; 4.


