
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие об исходном (ИП), и об исходном производящем контурах (ипк).Содержание книги
Поиск на нашем сайте
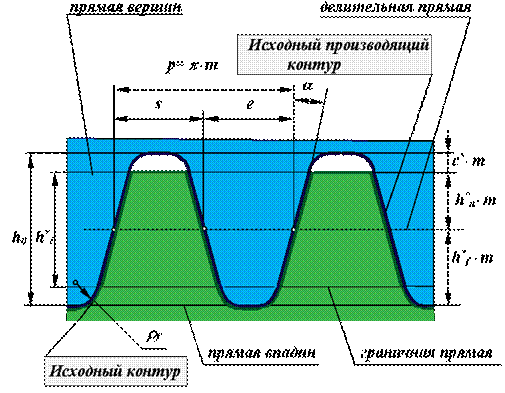
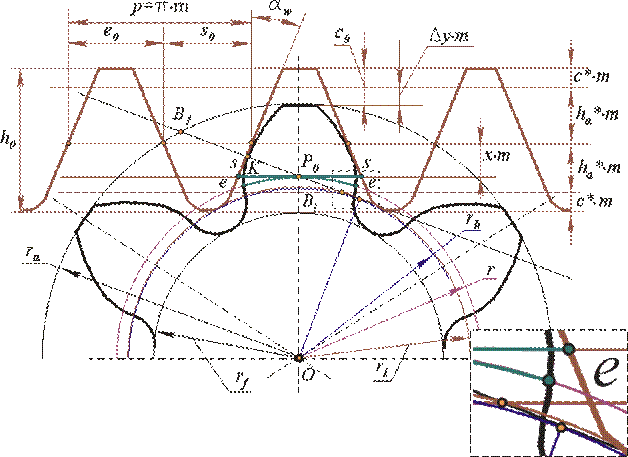
Рассмотрим формирование эвольвентного профиля методом обкатки. Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются: · для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения – исходный контур; · для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения – исходный производящий контур.
По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими: · угол главного профиля · коэффициент высоты зуба · коэффициент высоты ножки · коэффициент граничной высоты · коэффициент радиуса кривизны переходной кривой
· коэффициент радиального зазора в паре исходных контуров Исходный производящий контур отличается от исходного высотой зуба Исходный и исходный производящий контуры образуют между собой конгруэнтную пару (рис.1.3.), т.е. один заполняет другой как отливка заполняет заготовку (с радиальным зазором с *m в зоне прямой вершин зуба исходной рейки). Принципиальное отличие этих контуров в том, что исходный контур положен в основу стандартизации зубчатых колес, а исходный производящий – в основу стандартизации зуборезного инструмента. Оба эти контура необходимо отличать от производящего контура – проекции режущих кромок инструмента на плоскость перпендикулярную оси заготовки. 2. Расчет размеров зубчатого колеса. Определим основные размеры эвольвентного зубчатого колеса, используя схему обкатки зуба ИПП (рис.1.4.).
2.1. Радиус окружности вершин:
2.2. Высота зуба
2.3. Радиус окружности впадин
2.4. Толщина зуба по делительной окружности. 4. Контрольные вопросы. 1. В чем заключается принцип обкатки в зубчатом соединении? 2. Как определить радиус обкатки? 3. Обосновать применение эвольвентного профиля для обеспечения обкатки без трения? 4. Пояснить назначение ИП? 5. Что такое ИПК? 6. Перечислить характерные диаметры на схеме зубчатой передачи. 7. Как связан шаг и модуль шестерни? 8. Что такое линия зацепления? 9. Что такое подрезание зуба? 10. Для чего применяется смещение ИПК?
2. АНАЛИЗ И РАСЧЕТ КИНЕМАТИЧЕСКОЙ СХЕМЫ ПРЯМОЗУБОГО ЗАЦЕПЛЕНИЯ В ПЛАНЕТАРНОМ РЕДУКТОРЕ
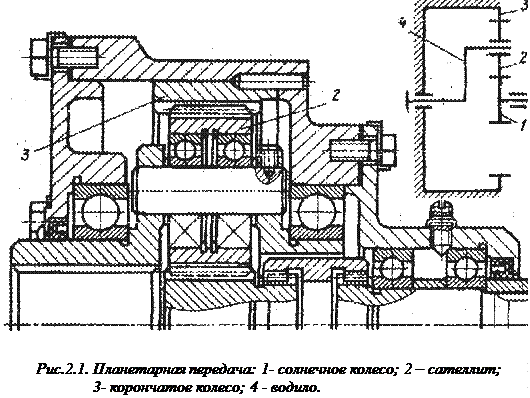
Лабораторная работа №2. (2часа) Цель: Освоить практические навыки анализа и расчета. Задачи: 1. Определить основные кинематические параметры одноступенчатого, однорядного планетарного редуктора. 2. Составить реальную схему передачи по рассчитанным величинам. 3. Найти условия работоспособности. Общие сведения. Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями (рис. 2.1.). Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.
Планетарные передачи имеют ряд преимуществ перед обычными: · большие передаточные отношения при малых габаритах и массе; · возможность сложения или разложения механической мощности; · лёгкое управление и регулирование скорости; · малый шум вследствие замыкания сил в механизме. В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом). Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач. Исходные данные. Мощность редуктора N, кВт; Частота вращения водил n н об/сек; Передаточное отношение i Схема редуктора
3.1. Угловая скорость на выходе и на входе:
3.2 Момент на входе и на выходе:
где: h = 0,98 – КПД. 3.3. Подбор числа зубьев солнечного колеса: Z 1 > 24. 3.4. Определение числа зубьев корончатого колеса:
3.5. Определение числа зубьев сателлита из условия соосности:
3.6. Выбор числа сателлитов с; 3.7 Проверка условия сборки:
где N – целое число. 3.8. Проверка выполнения условия соседства:
3.9. Определение крутящего момента, передаваемого от солнечного колеса сателлиту:
где: П = 0,005 – коэффициент потерь на трение в опорах качения; Кн = 1,42 – коэффициент неравномерности. 3.10. Определение передаточного отношения в планетарном редукторе
Результаты расчетов свести в таблицу.
3. ОПРЕДЕЛЕНИЕ РАБОТОСПОСОБНОСТИ КОНИЧЕСКОГО ЗАЦЕПЛЕНИЯ ПО УСЛОВИЯМ КОНТАКТНОЙ ВЫНОСЛИВОСТИ И ПРОЧНОСТИ НА ИЗГИБ ЗУБА
Лабораторная работа № 3 (4часа) Цель работы: Освоение практического навыка в расчете и определении работоспособности конической передачи. Задачи работы: 1. провести расчет кинематических параметров по исходным данным. 2. построить схему конического зацепления по полученным расчетным значениям диаметров колес. 3. оценить работоспособность передачи по условиям контактной выносливости и прочности на изгиб зуба. Выполнение задания по методикам учебника: Основы расчёта и конструирования деталей машин и механизмов /Под ред. В.Н. Кестельмана/ М.: Машиностроение, 1989. Исходные данные и схема зацепления. Торцевой модуль, mtm, мм; Число зубьев нашестерне Межосевой угол, S, град; Наклон зубьев к оси b, град; Угол исходного профиля a Момент сил на валу Скорость вращения n Передаточное отношение i. Профиль зубьев конических колес близок к эвольвентному профилю зубьев цилиндрического колеса, образованному разверткой среднего дополнительного конуса (рис. 3.1). Такое цилиндрическое колесо называется эквивалентным. Для конических колес с круговыми зубьями производится двойной переход к биэквивалентному колесу: в нормальном сечении среднего дополнительного конуса к профилю прямозубых колес с числом зубьев:
Передаточное число эквивалентной передачи равно:
Параметры биэквивалентных и эквивалентных колес используются в расчетах на прочность. 3.2. Рекомендуемый порядок определения кинематических параметров. 3.2.1. Определить делительные диаметры в торцевом внешнем и среднем сечениях:
3.2.2. Найти конусное расстояние:
где: ΨR = 3.2.3. Найти высоту головки hae и ножки hfe зуба; по внешнему торцу принимают равными: hae = mte, hfe = 1.2× mte. 3.2.4. Передаточное число конической передачи:
3.2.5. Частота вращения ведущего вала:
3.2.6. Угловая скорость вращения ведущего вала: 3.2.7. Вращающий момент на валу колеса:
3.2.8. Число зубьев для ведомого колеса:
3.2.9. Определение диаметров зубчатых колес: - диаметр начальной окружности: - внешний диаметр ведущего колеса: ведомого колеса: - средний диаметр ведущего колеса: ведомого колеса:
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

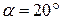 ;
;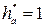 ;
;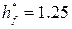 ;
;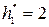 ;
;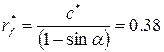 ;
;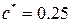 .
.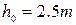 .
.
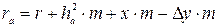 ;
; 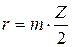 ;
;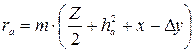 .
.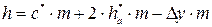 ;
;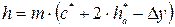 .
. .
.
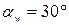 .
.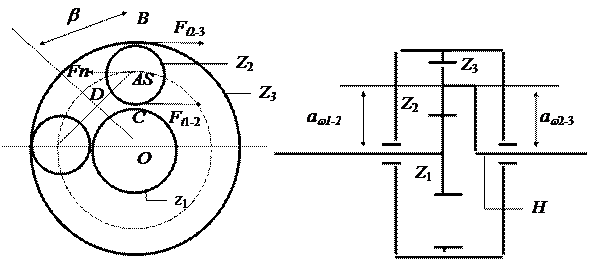 3. Порядок и содержание расчетов
3. Порядок и содержание расчетов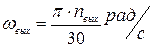 ;
;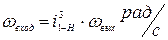 .
.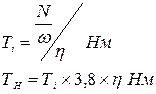 ;
;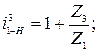
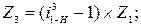
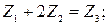
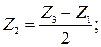
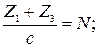
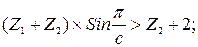
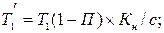
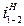 ,
, 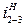 ,
, 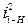 ,
, 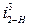 :
: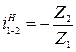 ;
; 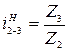 ;
; 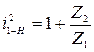 ;
; 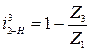 .
.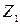 ;
;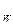 ;
;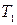 , Н∙м;
, Н∙м;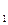 , об/мин;
, об/мин;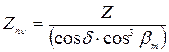 .
.
 .
.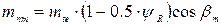
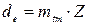 ,
, 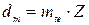 ,
,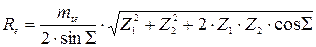
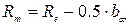
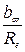 – относительная ширина зубчатого венца.
– относительная ширина зубчатого венца.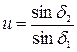 .
.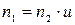 об/мин.
об/мин.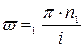 , рад/сек.
, рад/сек.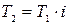 , Нм.
, Нм.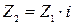 .
.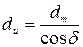 ;
;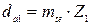 , мм;
, мм;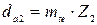 , мм;
, мм;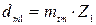 , мм;
, мм;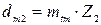 , мм.
, мм.


