
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сибирский государственный аэрокосмическийСодержание книги
Поиск на нашем сайте
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика Н.Ф.Решетнева (СибГАУ) Коваленко Г.Д.
ПРОЕКТНЫЕ РАСЧЕТЫ МЕХАНИЗМОВ ЛЕТАТАТЕЛЬНЫХ АППАРАТОВ . Практикум по дисциплине «Детали и механизмы летательных аппаратов»
Красноярск 2011 УДК 629.7.02.001.24(075.8)
Рецензенты Доктор технических наук, проф. А.Е. Михеев (зав каф. «Летательные аппараты», СибГАУ). Зам ген. Директора ООО Аэро Гео Зосимов Виталий Георгиевич
Коваленко Г.Д. Проектные расчеты механизмов летательных аппаратов: учебное пособие/ Г.Д. Коваленко. Сиб. гос. аэрокосм. ун-т. Красноярск, 2011. 80с.
Предлагаемый практикум рассчитан на студентов, проходящих курс «Детали и механизмы летательных аппаратов». Включает сведения, необходимые для проектных расчетов ряда механизмов при выполнении практических заданий и лабораторных работ, а также при курсовом и дипломном проектировании.
УДК629.7.02.001.24(075.8) СОДЕРЖАНИЕ
1. Построение эвольвентного профиля…………………………………….. 2. Анализ и расчет кинематической схемы прямозубого зацепления в планетарном редукторе…………………………………………………. 3. Определение работоспособности конического зацепления по условиям контактной выносливости и прочности на изгиб зуба…………………. 4. Расчёт червячной передачи………………………………………………. 5. Расчёт передачи винт-гайка………………………………………………. 6. Расчёт кривошипно-шатунного механизма…………………………….. 7. Приложение
ПОСТРОЕНИЕ ЭВОЛЬВЕНТНОГО ПРОФИЛЯ ЗУБЬЕВ ПРЯМОЗУБОЙ ПЕРЕДАЧИ
Лабораторная работа №1
Цель работы: п остроить эвольвентный профиль методом обкатки. Задачи работы: 1. По исходным данным сделать построения исходного производящего профиля (ИПК). 2. Имитируя обкатку ИПК из твердого картона, графически выполнить построения, по контуру заготовки зубчатого колеса, обрисовывая контур зубьев ИПК на каждой фазе перемещения без проскальзывания. 3. Выделить окончательно профиль зуба колеса. 4. Построить схему зацепления с численными значениями параметров. Теоретическая основа. Зацепление двух зубчатых колес с числами зубьев При эвольвентном профиле зубьев траектория точки контакта двух сопряженных профилей зубьев во время зацепления представляет собой прямую линию и называется линией зацепления (N-N).
Рис 1.1. Схема зацепления. Точка касания начальных окружностей и одновременно точка пересечения линии центров с линией зацепления называется полюсом зацепления (О). Угол между нормалью к линии центров, проведенной через полюс зацепления, и линией зацепления называют углом зацепления Окружность зубчатого колеса, делящуюся при его нарезании на равное число частей длиной Р, называемых шагами, и имеющую стандартный модуль, называют делительной. Диаметр такой окружности находят из равенства Сведения о профиле зуба. [mechfac.ru › attachments/150_]
Боковые грани зубьев, соприкасающиеся друг с другом во время вращения колес, имеют специальную криволинейную форму, называемую профилем зуба. Наиболее распространенным в машиностроении является эвольвентный профиль (рис.1.2.).
В основу профилирования эвольвентных зубьев и инструмента для их нарезания положен стандартный по ГОСТ 13755-81 исходный контур так называемой рейки, равный 20°. Если заменить одно из колес зубчатой рейкой, то для каждого зубчатого колеса найдется только одна окружность, катящаяся по начальной прямой рейке без скольжения, – эта окружность называется делительной. Примечание. В настоящей работе рассматриваются зубчатые передачи, у которых начальные и делительные окружности совпадают. Так как у каждого зубчатого колеса имеется только одна делительная окружность, то она и положена в основу определения основных параметров зубчатой передачи по ГОСТ 16530-83 и ГОСТ 16531-83. Существует множество вариантов изготовления зубчатых колес [ e-mail: KarimovI@rambler. ru ]. В их основу положены два принципиально отличных метода: · метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности (конгруентны ей, т. Е. заполняют эту поверхность как отливка заполняет форму); · метод обкатки, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения – резания и обкатки (под обкаткой понимается такое относительное движение заготовки и инструмента, которое соответствует станочному зацеплению, т. Е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения). Из вариантов изготовления по способу копирования можно отметить: · Нарезание зубчатого колеса профилированной дисковой или пальцевой фрезой (проекция режущих кромок которой соответствует конфигурации впадин). При этом методе резание производится в следующем прядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются пока не будут прорезаны все впадины. Производительность данного способа низкая, точность и качество поверхности невысокие. · Отливка зубчатого колеса в форму. При этом внутренняя поверхность литейной формы конгруентна наружной поверхности зубчатого колеса. Производительность и точность метода высокая, однако, при этом нельзя получить высокой прочности и твердости зубьев. · Из вариантов изготовления по способу обкатки наибольшее распространение имеют: · Обработка на зубофрезерных или зубодолбежных станках червячными фрезами или долбяками. Производительность достаточно высокая, точность изготовления и чистота поверхностей средняя. Можно обрабатывать колеса из материалов с невысокой твердостью поверхности. · Накатка зубьев с помощью специального профилированного инструмента. Обеспечивает высокую производительность и хорошую чистоту поверхности. Применяется для пластичных материалов, обычно на этапах черновой обработки. Недостаток метода образование наклепанного поверхностного слоя, который после окончания обработки изменяет свои размеры. · Обработка на зубошлифовальных станках дисковыми кругами. Применяемся как окончательная операция после зубонарезания (или накатки зубьев) и термической обработки. Обеспечивает высокую точность и чистоту поверхности. Применяется для материалов с высокой поверхностной прочностью. · Общие сведения. Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями (рис. 2.1.). Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.
Планетарные передачи имеют ряд преимуществ перед обычными: · большие передаточные отношения при малых габаритах и массе; · возможность сложения или разложения механической мощности; · лёгкое управление и регулирование скорости; · малый шум вследствие замыкания сил в механизме. В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом). Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач. Исходные данные. Мощность редуктора N, кВт; Частота вращения водил n н об/сек; Передаточное отношение i Схема редуктора
3.1. Угловая скорость на выходе и на входе:
3.2 Момент на входе и на выходе:
где: h = 0,98 – КПД. 3.3. Подбор числа зубьев солнечного колеса: Z 1 > 24. 3.4. Определение числа зубьев корончатого колеса:
3.5. Определение числа зубьев сателлита из условия соосности:
3.6. Выбор числа сателлитов с; 3.7 Проверка условия сборки:
где N – целое число. 3.8. Проверка выполнения условия соседства:
3.9. Определение крутящего момента, передаваемого от солнечного колеса сателлиту:
где: П = 0,005 – коэффициент потерь на трение в опорах качения; Кн = 1,42 – коэффициент неравномерности. 3.10. Определение передаточного отношения в планетарном редукторе
Результаты расчетов свести в таблицу.
3. ОПРЕДЕЛЕНИЕ РАБОТОСПОСОБНОСТИ КОНИЧЕСКОГО ЗАЦЕПЛЕНИЯ ПО УСЛОВИЯМ КОНТАКТНОЙ ВЫНОСЛИВОСТИ И ПРОЧНОСТИ НА ИЗГИБ ЗУБА
Лабораторная работа № 3 (4часа) Цель работы: Освоение практического навыка в расчете и определении работоспособности конической передачи. Задачи работы: 1. провести расчет кинематических параметров по исходным данным. 2. построить схему конического зацепления по полученным расчетным значениям диаметров колес. 3. оценить работоспособность передачи по условиям контактной выносливости и прочности на изгиб зуба. Выполнение задания по методикам учебника: Основы расчёта и конструирования деталей машин и механизмов /Под ред. В.Н. Кестельмана/ М.: Машиностроение, 1989. Исходные данные и схема зацепления. Торцевой модуль, mtm, мм; Число зубьев нашестерне Межосевой угол, S, град; Наклон зубьев к оси b, град; Угол исходного профиля a Момент сил на валу Скорость вращения n Передаточное отношение i. Профиль зубьев конических колес близок к эвольвентному профилю зубьев цилиндрического колеса, образованному разверткой среднего дополнительного конуса (рис. 3.1). Такое цилиндрическое колесо называется эквивалентным. Для конических колес с круговыми зубьями производится двойной переход к биэквивалентному колесу: в нормальном сечении среднего дополнительного конуса к профилю прямозубых колес с числом зубьев:
Передаточное число эквивалентной передачи равно:
Параметры биэквивалентных и эквивалентных колес используются в расчетах на прочность. 3.2. Рекомендуемый порядок определения кинематических параметров. 3.2.1. Определить делительные диаметры в торцевом внешнем и среднем сечениях:
3.2.2. Найти конусное расстояние:
где: ΨR = 3.2.3. Найти высоту головки hae и ножки hfe зуба; по внешнему торцу принимают равными: hae = mte, hfe = 1.2× mte. 3.2.4. Передаточное число конической передачи:
3.2.5. Частота вращения ведущего вала:
3.2.6. Угловая скорость вращения ведущего вала: 3.2.7. Вращающий момент на валу колеса:
3.2.8. Число зубьев для ведомого колеса:
3.2.9. Определение диаметров зубчатых колес: - диаметр начальной окружности: - внешний диаметр ведущего колеса: ведомого колеса: - средний диаметр ведущего колеса: ведомого колеса: Общие сведения. Геометрические расчеты аналогичны расчетам зубчатых передач, так как червяк является подобием косозубого эвольвентного колеса, у которого число зубьев равно числу витков резьбы. По числу винтовых линий резьбы червяк может быть однозаходным и многозаходным. С увеличением числа заходов возрастает угол подъема винтовой линии и повышается КПДпередачи. Однозаходные червяки применяют, когда необходимы большие передаточные числа или самоторможение. Червяки имеют обычно правую нарезку, кроме случаев, обусловленных требованиями кинематики. В зависимости от положения червяка относительно червячного колеса передачи бывают с верхним и нижним расположением червяка. При нижнем расположении условия для смазки лучше. Основные геометрические параметры червячной передачи: модуль Угол подъема винтовой линии определяют из соотношения
В цилиндрических передачах с архимедовым червяком шаг червяка Р и шаг зубьев червячного колеса совпадают. Геометрические размеры червяка и червячного колеса (рис. 4.1.) приведены в табл.4.1. ( В целях ограничения номенклатуры стандартного инструмента для нарезания червячных колес и червяков значения т, q, т, мм 1,0; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; q 6,3: 8; 10 (кроме т = 2); 12,5 (кроме т = 2,5); 16; 20;
Таблица 4.1. Исходные данные. Момент на оси червячного колеса. Передаточное отношение i; Число заходов червяка Материал червячного колеса при
Проектный расчет. ( пример) 3.1. Расчет геометрии червячной передачи. Ориентировочной значение межосевого расстояния определяется по формуле:
Например: Таблица 4.2. Общие сведения. Передачи винт-гайка предназначены для преобразования вращательного движения в поступательное. Их широко применяют в механизмах управления ЛА. Так, они используются в механизмах управления внутренними и внешними закрылками, предкрылками, рулями высоты и направления, в механизмах изменения стреловидности крыла, выпуска шасси и т. П. Передачи винт-гайка при значительной несущей способности имеют небольшие габаритные размеры и массу, позволяют с малым вращающим моментом создать большую осевую силу и обеспечивают высокую точность требуемого закона движения. Передачи винт-гайка по характеру движения звеньев разделяют на: · передачи с ведущим вращающимся винтом, совершающим одновременно осевое перемещение. Такие передачи применяют при незначительных перемещениях, например в измерительной Технике; · · передачи с вращающейся гайкой и ведомым поступательно перемещающимся винтом (рис. 5.2.). Такие передачи применяется при небольших перемещениях и значительных осевых силax на винте, например в механизмах управления стабилизаторами-нервюрами ЛА. Передачи винт-гайка по виду трения делятся на передачи скольжения и качения.
Эти передачи при значительной несущей способности, небольших габаритных размерах и массе конструктивно просты и технологичны в изготовлении. Для механизмов управления ЛА важно, что при однозаходной резьбе такие передачи обеспечивают самоторможение. Недостатками передач винт-гайка с трением скольжения являются низкий КПД (0.25 …0.40 при однозаходных резьбах) и невозможность использования ее при высоких скоростях поступательного движения гайки или винта, так как скорость скольжения витков гайки относительно витков винта в 10… 40 раз превышает скорость осевого перемещения, что ведет к повышенному износу и перегреву механизма. В силовых реверсивных передачах винт-гайка скольжения, характерных для механизмов управления ЛА, чаще всего применяют трапецеидальную резьбу (рис. 5.3, а),обладающую высокой прочностью витков, технологичностью изготовления и меньшими по сравнению с метрической треугольной потерями на трение. Метрическую резьбу мелкого шага (рис. 5.3, б) применяют для получения точных перемещений в механизмах приборов. Резьба характеризуется наружным Для трапецеидальной резьбы профиль и основные ее размеры гостированы: Для метрической резьбы эти параметры даны в ГОСТ 8724-71. Для каждого диаметра резьбы указаны основной и мелкий шаги. Резьба ходовых винтов и гаек в зависимости от назначения передачи может быть правой и левой, одно- или многозаходной.
Передачи винт-гайка с трением качения. Передачи винт-гайка с трением качения широко применяют в силовых и приборных механизмах ЛА. Усилие между винтом и гайкой передается через шарики, которые перемещаются в винтовых дорожках качения, выполненных на винте и в гайке. Скорость перемещения этих шариков отличается от скорости ведущего и ведомого звеньев, поэтому для обеспечения непрерывной циркуляции шариков концы рабочей части резьбы в гайке соединены возвратным каналом. Шарико-винтовые механизмы (ШВМ) применяются для рабочих нагрузок от сотен до сотен тысяч ньютон. Средние диаметры винтов в этих механизмах 5… 150 мм, диаметры шариков 1…20 мм. ШВМ имеют ряд преимуществ перед обычными передачами винт-гайка скольжения: малые потери мощности на трение качения, позволяющие повышать КПД механизма до 0,9; низкий приведенный коэффициент трения покоя и, следовательно, высокая кинематическая чувствительность; малый износ рабочих винтовых поверхностей винта и гайки, обеспечивающий высокую точность и равномерность поступательного движения с сохранением стабильности этих параметров в процессе эксплуатации; надежная работа в широком диапазоне температур и вакууме. К недостаткам ШВМ относят относительную сложность и трудоемкость изготовления. Особенно трудоемкой является операция шлифования специального профиля резьбы гайки и ходового винта. Однако с появлением станков для шлифования профиля резьбы винта и гайки и разработкой более совершенных методов обработки деталей этот недостаток устраняется. В ШВМ различного назначения применяют криволинейные профили резьбы винта и гайки (рис.5.4, а, в),прямолинейные (рис.5.4, г, д, е)и комбинированные (рис. 5.4, б).Для силовых ШВМ, применяемых в ЛА, рекомендуют полукруглые Профили с двухточечным контактом и углом контакта Высокий КПД, надежность ШВМ в значительной степени зависят от конструкции и качества изготовления перепускного канала. Каналы должны быть просты в изготовлении и допусать регулировку элемента, направляющего шарики из резьбовой канавки в возвратный канал; иметь плавный переход резьбовой канавки в возвратный канал; обеспечивать минимальный путь возврата шарика при малом числе поворотов. Одним из распространенных способов перепуска является перепуск шариков по изогнутой трубке, соединяющей начало и конец винтовой канавки гайки (рис.5.5, а). Шарики направляются в трубку либо концом самой трубки, либо специальными отражателями в корпусе гайки около концов трубки. Существенным недостатком таких конструкций возврата шариков является увеличение радиальных размеров гайки.
Твердость контактирующих поверхностей резьбы винта и гайки определяет нагрузочную способность и долговечность ШВМ. Она должна быть не ниже 60 HRC. В случае поверхностного упрочнения (азотирования, объемной закалки после цементации или закалки ТВЧ) толщина слоя должна быть достаточной для восприятия высоких контактных напряжений. Винты изготовляют из сталей ХВГ и 7ХГ2ВМ с объемной закалкой, 8ХВ с закалкой при индукционном нагреве и 20ХЗМВФ с азотированием поверхности. Для гаек применяют стали марок 9ХС, ШХ15 с объемной закалкой и цементируемые стали 18ХГТ, 12ХНЗА, 18ХНВА и др. Шарики обычно изготавливают из стали ШХ15, ШХ15СГ. Твердость поверхности шариков должна быть не ниже 63 HRC. Схемы закрепления опор.
Примечание. Опоры скольжения при Для винтов любой гибкости удобно пользоваться объединенным условием прочности и устойчивости
где:
выбираемый в зависимости от параметра гибкости:
КПД винтовой пары в случае преобразования вращательного движения в поступательное равен
КПД передач винт-гайка с трением скольжения невысок. При Условие самоторможения в винтовых передачах Порядок расчета. Расчет силовых ШВМ существенно отличается от расчета передач винт-гайка с трением скольжения. Его геометрические размеры определяют исходя из нагрузочной способности, основываясь на зависимости размеров механизма в зоне контакта шариков от величины допускаемых контактных напряжений и числа циклов нагружения. Диаметр винта выбирают, прежде всего, из условия устойчивости винта. Внутренний диаметр резьбы винта
При проектном расчете диаметр шарика
Ходовой винт ШВМ проверяют на прочность при сложном напряженном состоянии. Определяют крутящий момент
где:
k – коэффициент терния качения в шариковинтовой паре,
Таблица 5.2 Таблица параметров ШВМ.
Проверка винта на продольную устойчивость (см. 5.13). КПД ШВМ при преобразовании вращательного движения в поступательное определяется по формуле (5.16) с заменой У ШВМ, работающих при значительных нагрузках, деформация его элементов вызывает наряду с трением качения трение скольжения. В этом случае действительные значения КПД будут на 6...8 % ниже. Влияние трения скольжения на КПД тяжело нагруженного ШВМ можно учесть с помощью коэффициента Условие самоторможения в ШВМ имеет вид
Расчеты
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.152 (0.011 с.) |

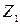 и
и 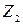 можно представить как качение без скольжения двух окружностей диаметрами
можно представить как качение без скольжения двух окружностей диаметрами  и
и  называемых начальными. Эти окружности определяют диаметры двух цилиндров, называемых начальными (рис.1.1.). Параметрам шестерни согласно стандартам присваивают индекс «1», а параметрам колеса – «2». У параметров зубчатых колес индекс «w» относится к начальной поверхности (окружности), «а» – к поверхности (окружности) вершин и к головке зуба, «f» – к поверхности (окружности) впадин и ножке зуба.
называемых начальными. Эти окружности определяют диаметры двух цилиндров, называемых начальными (рис.1.1.). Параметрам шестерни согласно стандартам присваивают индекс «1», а параметрам колеса – «2». У параметров зубчатых колес индекс «w» относится к начальной поверхности (окружности), «а» – к поверхности (окружности) вершин и к головке зуба, «f» – к поверхности (окружности) впадин и ножке зуба.
 , для стандартного зацепления
, для стандартного зацепления  .
.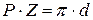 , откуда:
, откуда:  . [1]
. [1] Придание профилям зубьев зубчатых зацеплений таких очертаний не является случайностью. Чтобы зубья двух колес, находящихся в зацеплении, могли плавно перекатываться один по другому, необходимо было выбрать такой профиль для зубьев, при котором не происходило бы перекосов и защемления головки одного зуба во впадине другого.
Придание профилям зубьев зубчатых зацеплений таких очертаний не является случайностью. Чтобы зубья двух колес, находящихся в зацеплении, могли плавно перекатываться один по другому, необходимо было выбрать такой профиль для зубьев, при котором не происходило бы перекосов и защемления головки одного зуба во впадине другого.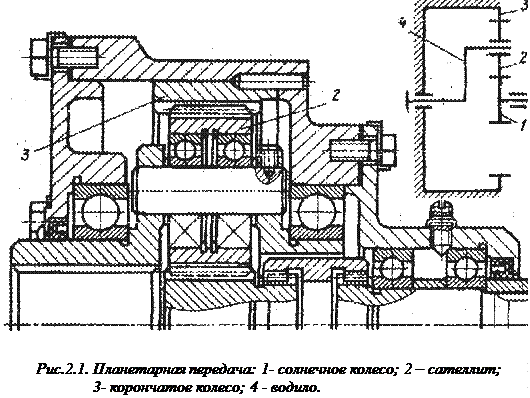
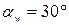 .
.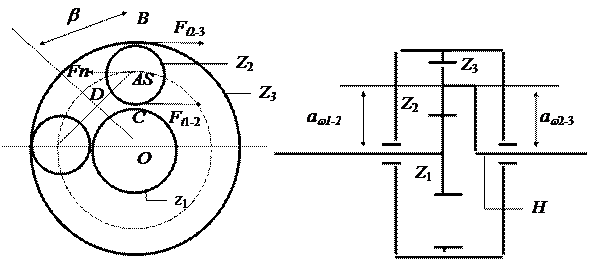 3. Порядок и содержание расчетов
3. Порядок и содержание расчетов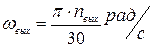 ;
;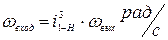 .
.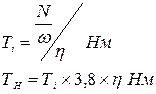 ;
;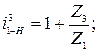
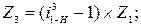
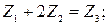
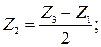
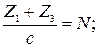
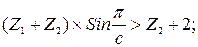
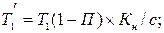
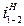 ,
, 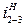 ,
, 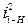 ,
, 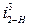 :
: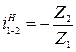 ;
; 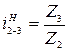 ;
; 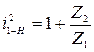 ;
; 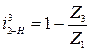 .
.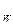 ;
;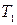 , Н∙м;
, Н∙м;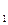 , об/мин;
, об/мин;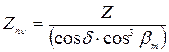 .
.
 .
.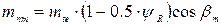
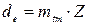 ,
, 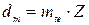 ,
,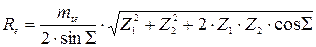
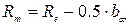
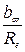 – относительная ширина зубчатого венца.
– относительная ширина зубчатого венца.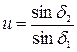 .
.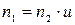 об/мин.
об/мин.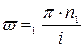 , рад/сек.
, рад/сек.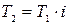 , Нм.
, Нм.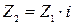 .
.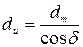 ;
;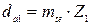 , мм;
, мм;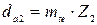 , мм;
, мм;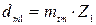 , мм;
, мм;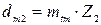 , мм.
, мм.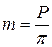 ;коэффициент диаметра червяка q; шаг резьбы червяка в осевом сечении P. Делительный диаметр червяка d
;коэффициент диаметра червяка q; шаг резьбы червяка в осевом сечении P. Делительный диаметр червяка d 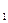 связан с модулем т коэффициентом диаметра червяка:
связан с модулем т коэффициентом диаметра червяка: 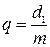 . Для многозаходных червяков ход
. Для многозаходных червяков ход 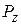 связан с шагом Р соотношением:
связан с шагом Р соотношением: 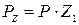 ,где
,где 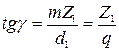 .
.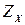 стандартизированы. Рекомендации по выбору т, q, Z приведены ниже (угол профиля в осевом сечении также стандартизирован: α = 20 °):
стандартизированы. Рекомендации по выбору т, q, Z приведены ниже (угол профиля в осевом сечении также стандартизирован: α = 20 °):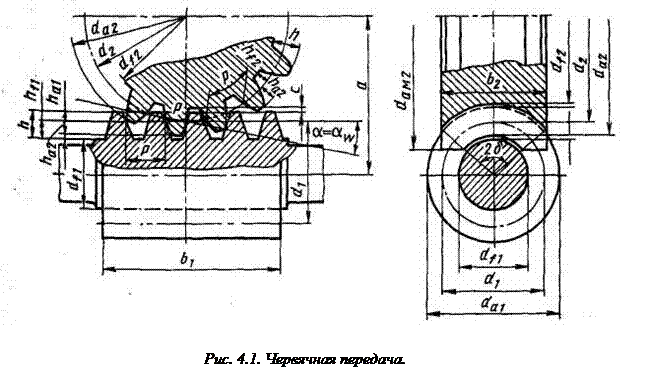
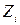 1; 2; 4.
1; 2; 4. ,
,  ;
;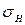 , Мпа.
, Мпа. ,
,
 Мпа;
Мпа;  .
. передачи с вращающимся винтом и ведомой, поступательно перемещающейся гайкой (рис. 5.1.). Такая схема обычно используется в силовых передачах при больших перемещениях, например в механизме изменения стреловидности крыла самолета (рис. 5.1.). Такие передачи в механизмах управления ЛА обычно применяют одновременно с зубчатой передачей, понижающей частоту вращения винта;
передачи с вращающимся винтом и ведомой, поступательно перемещающейся гайкой (рис. 5.1.). Такая схема обычно используется в силовых передачах при больших перемещениях, например в механизме изменения стреловидности крыла самолета (рис. 5.1.). Такие передачи в механизмах управления ЛА обычно применяют одновременно с зубчатой передачей, понижающей частоту вращения винта; Передачи винт-гайка с трением скольжения.
Передачи винт-гайка с трением скольжения. , внутренним
, внутренним  и средним
и средним 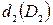 диаметрами (d относится к винту, D – к гайке); шагом резьбы Р; теоретической высотой профиля Н; рабочей высотой профиля
диаметрами (d относится к винту, D – к гайке); шагом резьбы Р; теоретической высотой профиля Н; рабочей высотой профиля 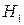 ; углом профиля
; углом профиля 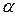 ; числом заходов Z, ходом резьбы
; числом заходов Z, ходом резьбы  , углом подъема резьбы
, углом подъема резьбы  .
. ; Hi = 0,5 P;
; Hi = 0,5 P;  ;
;  мм;
мм; 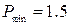 мм.
мм.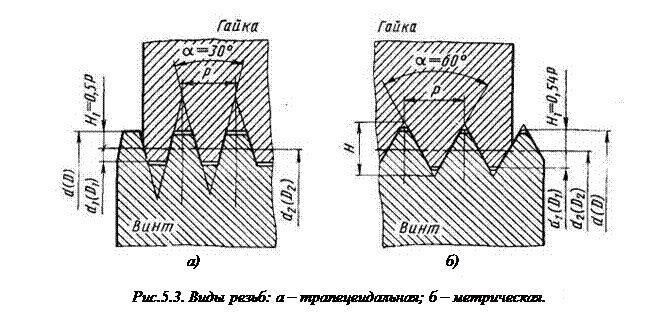 Ходовые винты передач винт-гайка скольжения изготовляют из сталей, обладающих высокой прочностью и износостойкостью. При числах твердости поверхности не более 350 НВ –из сталей 45, 50 и др.; при числах твердости не менее 50 HRC –из сталей 65Г, 45Х, 40ХН, 12ХНЗА и др. Для уменьшения потерь на трение гайки выполняют из антифрикционных оловянистых (БрОФЮ-1, БрОЦС6-6-3) и безоловянистых (БрАЖ9-4, БрАЖМцО-3-1.5) бронз, способных воспринимать большие удельные нагрузки и обладающих антикоррозионными свойствами и хорошей прирабатываемостью. Оловянистые бронзы применяются при окружных скоростях
Ходовые винты передач винт-гайка скольжения изготовляют из сталей, обладающих высокой прочностью и износостойкостью. При числах твердости поверхности не более 350 НВ –из сталей 45, 50 и др.; при числах твердости не менее 50 HRC –из сталей 65Г, 45Х, 40ХН, 12ХНЗА и др. Для уменьшения потерь на трение гайки выполняют из антифрикционных оловянистых (БрОФЮ-1, БрОЦС6-6-3) и безоловянистых (БрАЖ9-4, БрАЖМцО-3-1.5) бронз, способных воспринимать большие удельные нагрузки и обладающих антикоррозионными свойствами и хорошей прирабатываемостью. Оловянистые бронзы применяются при окружных скоростях 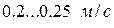 . При окружных скоростях, меньших
. При окружных скоростях, меньших  , применяют безоловянные бронзы, которые менее дефицитны, но имеют по сравнению с оловянными бронзами больший коэффициент трения в паре со сталью.
, применяют безоловянные бронзы, которые менее дефицитны, но имеют по сравнению с оловянными бронзами больший коэффициент трения в паре со сталью. (рис.5.4, а).Прямолинейный профиль резьбы (треугольный, трапециевидный) является наиболее технологичным, но значительно уступает по нагрузочной способности криволинейному. Это объясняется тем, что допускаемая нагрузка на шарик, находящийся в желобе с профилем в виде дуги окружности, более чем в три раза выше допускаемой нагрузки на шарик, лежащий на плоской поверхности трапецеидального или Треугольного профиля. Прямолинейный профиль резьбы применяют в ШВМ для восприятия небольших осевых нагрузок, например в приборах. В измерительных устройствах с высокими требованиями к точности перемещения узла рекомендуются ШВМ с прямоугольным профилем и трехточечным контактом между шариком и элементами винта и гайки (см. рис. 5.4, г, д).При таком контакте положение шарика определяется однозначно.
(рис.5.4, а).Прямолинейный профиль резьбы (треугольный, трапециевидный) является наиболее технологичным, но значительно уступает по нагрузочной способности криволинейному. Это объясняется тем, что допускаемая нагрузка на шарик, находящийся в желобе с профилем в виде дуги окружности, более чем в три раза выше допускаемой нагрузки на шарик, лежащий на плоской поверхности трапецеидального или Треугольного профиля. Прямолинейный профиль резьбы применяют в ШВМ для восприятия небольших осевых нагрузок, например в приборах. В измерительных устройствах с высокими требованиями к точности перемещения узла рекомендуются ШВМ с прямоугольным профилем и трехточечным контактом между шариком и элементами винта и гайки (см. рис. 5.4, г, д).При таком контакте положение шарика определяется однозначно.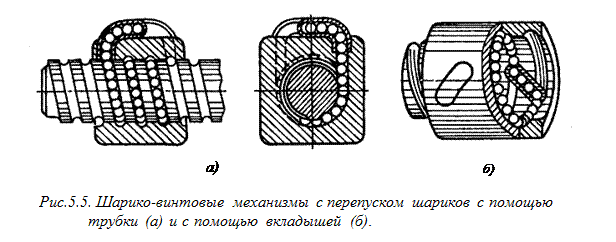 Более рациональной является конструкция, в которой возврат шариков осуществляется с помощью специальных вкладышей, вставленных в окна гайки по диагонали и соединяющих соседние винтовые канавки ее резьбы (рис. 5.5 б). Обычно в гайке предусматривают три вкладыша, которые располагают под углом 120°, причем шарики разделены на три независимо циркулирующие группы.
Более рациональной является конструкция, в которой возврат шариков осуществляется с помощью специальных вкладышей, вставленных в окна гайки по диагонали и соединяющих соседние винтовые канавки ее резьбы (рис. 5.5 б). Обычно в гайке предусматривают три вкладыша, которые располагают под углом 120°, причем шарики разделены на три независимо циркулирующие группы.




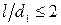 и опоры качения с одним подшипником эквивалентны шарнирной опоре; гайки с опорой рассматриваются как заделка.
и опоры качения с одним подшипником эквивалентны шарнирной опоре; гайки с опорой рассматриваются как заделка.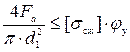 , (5.15)
, (5.15) – допускаемое напряжение для винтов передач,
– допускаемое напряжение для винтов передач, 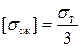 ;
;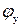 – коэффициент понижения допускаемых напряжений на сжатие,
– коэффициент понижения допускаемых напряжений на сжатие,
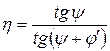 . (5.16)
. (5.16)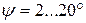 и
и 
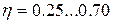 .
. выполняется только в винтовых передачах с однозаходными резьбами.
выполняется только в винтовых передачах с однозаходными резьбами.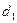 определяют по формуле:
определяют по формуле: . (5.17)
. (5.17)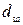 , шаг резьбы Р, средний диаметр резьбы
, шаг резьбы Р, средний диаметр резьбы 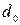 , наружный диаметр резьбы гайки
, наружный диаметр резьбы гайки 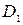 , радиус профиля каналов в винте и гайке
, радиус профиля каналов в винте и гайке  ; угол подъема винтовой линии резьбы
; угол подъема винтовой линии резьбы  на среднем диаметре (рис. 5.6.) можно выбирать в зависимости от
на среднем диаметре (рис. 5.6.) можно выбирать в зависимости от  по табл.5.2. Для полукруглого профиля
по табл.5.2. Для полукруглого профиля 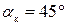 . Диаметр отверстия в гайке D и наружный диаметр резьбы винта d находят по формулам:
. Диаметр отверстия в гайке D и наружный диаметр резьбы винта d находят по формулам: ; (5.18)
; (5.18)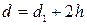 , (5.19)
, (5.19) где:
где:  ,
, 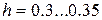 ; меньшее значение
; меньшее значение 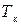 , приложенный к ходовому винту для преодоления осевой нагрузки. В ШВМ учитывают момент трения в шарикоподшипниках винта
, приложенный к ходовому винту для преодоления осевой нагрузки. В ШВМ учитывают момент трения в шарикоподшипниках винта  , который сравним по величине с моментом трения в шарико-винтовой паре
, который сравним по величине с моментом трения в шарико-винтовой паре  . Тогда
. Тогда , (5.20)
, (5.20)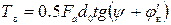 ;
; 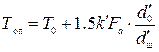 ;
; – приведенный угол трения качения,
– приведенный угол трения качения,  ;
;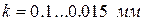 ;
;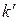 – коэффициент трения качения в шарикоподшипниках винта,
– коэффициент трения качения в шарикоподшипниках винта, мм;
мм; – момент трения ненагруженного шарикоподшипника,
– момент трения ненагруженного шарикоподшипника, 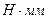 ,
, ;
;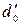 – средний диаметр шарикоподшипника,
– средний диаметр шарикоподшипника, 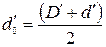 ;
; – диаметр шарика шарикоподшипника;
– диаметр шарика шарикоподшипника;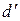 ,
, 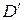 – внутренний и наружный диаметры подшипника.
– внутренний и наружный диаметры подшипника. , мм
, мм
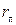 , мм
, мм
 на
на  . Так как
. Так как 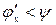 , то КПД шариковой передачи даже при малых углах подъема винтовой линии достигает 80...90 %.
, то КПД шариковой передачи даже при малых углах подъема винтовой линии достигает 80...90 %. . Величина
. Величина  зависит от нагрузки и твердости контактирующих тел,
зависит от нагрузки и твердости контактирующих тел,  .
. , (5.21)
, (5.21)


