
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умови рівноваги вільного твердого тілаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оскільки довільна система сил, прикладена до твердого тіла, еквівалентна головному вектору і головному моменту, то механічні умови рівноваги тіла полягають у рівності нулеві головного вектора і головного моменту системи сил:
Згідно з виразами (1.36) і (1.37) на підставі (1.38) дістаємо шість аналітичних умов рівноваги твердого тіла під дією довільної системи сил:
Умови (1.39) і (1.40) є наслідками з механічних умов рівноваги і формулюється так: Абсолютно тверде тіло перебуває у рівновазі лише тоді, коли алгебраїчні суми проекцій усіх сил на координатні осі й алгебраїчні суми моментів усіх сил відносно координатних осей дорівнюють нулеві. Таким чином, умови (1.39) і (1 40) дають шість рівнянь рівноваги вільного твердого тіла під дією довільної просторової системи сил. На підставі виразів (1.39) і (1.40) дістанемо рівняння рівноваги вільного твердого тіла, яке перебуває під дією довільної системи сил на площині. Припустимо, що ця система сил лежить на площині
Останнє рівняння (1.41) можна розглядати, з одного боку, як алгебраїчну суму моментів сил відносно осі Зауваження. Рівняння рівноваги (1.41) можна скласти в інших формах. Не зупиняючись на доведенні умов достатності вказаних способів, наведемо ці форми рівнянь рівноваги. Якщо вважати рівняння рівноваги у вигляді (1.41) першим варіантом, то другий варіант рівнянь полягатиме у рівності нулеві однієї суми проекції сил на будь-яку вісь, наприклад, на вісь
(умови достатності виконуються у випадку, коли Третій варіант полягає у рівності нулеві сум моментів сил відносно трьох точок площини:
(точки Якщо на тіло діє просторова система паралельних сил, то, припустивши, що сили паралельні осі
бо перші два рівняння виконуються тотожно, оскільки
Отже, Довільна система паралельних сил зрівноважується, якщо алгебраїчна сума проекцій сил на вісь, паралельну їхнім лініям дії, і алгебраїчні суми моментів сил відносно двох інших осей дорівнюють нулеві.
Приклади Приклад 1.3. На балку Розв’язання. 1. Як згадувалося раніше, спочатку треба виділити тіло, рівновагу якого розглядаємо. Таким тілом є балка 2. Аналізуємо сили. На балку діють сили

б Рисунок 1.22
На балку діє довільна система сил, розміщена на площині 3. Складемо рівняння рівноваги у вигляді (1.41):
У третьому рівнянні центр моментів взято у точці 4. Розв’язуючи систему рівнянь рівноваги, дістанемо
5. Аналізуючи розв’язок задачі (здобуті значення
Приклад 1.4. На вертикальну балку Нехтуючи вагою конструкції, знайти реакції опор Розв’язання. Насамперед треба замінити розподілене навантаження зосередженою силою
Лінія дії сили
в Рисунок 1.23
Отже, на конструкцію діють сили Оскільки сила тиску між балками є внутрішньою силою відносно системи з двох балок, то для її знаходження треба провести переріз між балками, і одну з них розглядати як в’язь. Розглянемо, наприклад, балку Складаємо три рівняння рівноваги:
З цієї системи знаходимо:
Від’ємний знак Тепер розглянемо балку Звільнимо балку Задача визначення Складаємо рівняння рівноваги:
Звідси
Приклад 1.5. Однорідний стержень Розв’язання. Розглядаючи рівновагу стержня
Рисунок 1.24 На балку діє система сил на площині (три невідомі сили Початок системи координат вибираємо в точці Складаємо рівняння рівноваги:
Згідно з (1.1.7)
і далі
Натяг Остаточно
Приклад 1.6. Однорідна прямокутна полиця вагою Розв’язання. Розглянемо рівновагу
Рисунок 1.25 Натяг
Після розв’язання цієї системи знаходимо:
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.009 с.) |

 ;
;  . (1.38)
. (1.38) ;
;  ;
;  ; (1.39)
; (1.39) (1.40)
(1.40) . Тоді всі координати
. Тоді всі координати  точок прикладання сил дорівнюють нулеві, проекції
точок прикладання сил дорівнюють нулеві, проекції  усіх сил також тотожно дорівнюють нулеві. Із шести рівнянь рівноваги (1.39) і (1.40) три тотожно дорівнюють нулеві. Залишилося три рівняння рівноваги:
усіх сил також тотожно дорівнюють нулеві. Із шести рівнянь рівноваги (1.39) і (1.40) три тотожно дорівнюють нулеві. Залишилося три рівняння рівноваги: ;
; . (1.41)
. (1.41) , перпендикулярної до площини
, перпендикулярної до площини 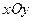 , а з другого – як суму моментів усіх сил відносно початку координат, тобто відносно довільної точки площини
, а з другого – як суму моментів усіх сил відносно початку координат, тобто відносно довільної точки площини  і суми моментів сил відносно двох точок площини:
і суми моментів сил відносно двох точок площини:

 (1.42)
(1.42) не перпендикулярна до
не перпендикулярна до  ).
). ;
;  . (1.43)
. (1.43) не лежать на одній прямій).
не лежать на одній прямій). , з (1.39)дістанемо
, з (1.39)дістанемо , (1.44)
, (1.44) ,
,  . З умов (1.40) залишаються такі:
. З умов (1.40) залишаються такі: ;
;  . (1.45)
. (1.45)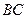 діють сили
діють сили  Н,
Н,  Н і пара сил з моментом
Н і пара сил з моментом  Н×м (рис. 1.22). Нехтуючи вагою балки і тертям, знайти реакції опор.
Н×м (рис. 1.22). Нехтуючи вагою балки і тертям, знайти реакції опор. і
і  і пара сил з моментом
і пара сил з моментом  На підставі аксіоми про звільнення від в’язей, відкинемо всі в’язі – нерухому
На підставі аксіоми про звільнення від в’язей, відкинемо всі в’язі – нерухому 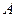 і рухому
і рухому  опори – і їхню дію позначаємо відповідними реакціями: реакція
опори – і їхню дію позначаємо відповідними реакціями: реакція  рухомого шарніра В напрямлена перпендикулярно до похилої площини, тому що тертя відсутнє; реакція
рухомого шарніра В напрямлена перпендикулярно до похилої площини, тому що тертя відсутнє; реакція  нерухомого шарніра
нерухомого шарніра  .
. , до складу якої входять три невідомі сили (скалярні величини):
, до складу якої входять три невідомі сили (скалярні величини):  . Для такої системи можна скласти три рівняння рівноваги. Отже, задача статично визначена.
. Для такої системи можна скласти три рівняння рівноваги. Отже, задача статично визначена.
 і
і  відносно точки
відносно точки  .
.
 і
і  ), зауважимо, що всі вони додатні, тому мають ті самі напрямки, які показано на рис. 1.22, б. Реакція нерухомої опори
), зауважимо, що всі вони додатні, тому мають ті самі напрямки, які показано на рис. 1.22, б. Реакція нерухомої опори кН.
кН. , яка жорстко закріплена в точці
, яка жорстко закріплена в точці  , яка в точці
, яка в точці 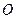 закріплена за допомогою нерухомого шарніра і вільно спирається на
закріплена за допомогою нерухомого шарніра і вільно спирається на  , діє сила
, діє сила  кН, яка напрямлена перпендикулярно до балки
кН, яка напрямлена перпендикулярно до балки  м;
м;  м;
м;  м.
м. , яка еквівалентна навантаженню і прикладена в центрі ваги цього навантаження. За модулем сила
, яка еквівалентна навантаженню і прикладена в центрі ваги цього навантаження. За модулем сила  =18 кН.
=18 кН. горизонтальна і віддалена від
горизонтальна і віддалена від  на
на  , тобто на 4 м.
, тобто на 4 м.


 і
і 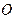 розкладаємо на
розкладаємо на  і
і  , реакція балки
, реакція балки 
 кН;
кН;  кН;
кН; кН.
кН. свідчить, що проекція напрямлена у від’ємний бік осі
свідчить, що проекція напрямлена у від’ємний бік осі  м) діє сила
м) діє сила  , яка дорівнює
, яка дорівнює  , але протилежно їй напрямлена (рис. 1.25, в).
, але протилежно їй напрямлена (рис. 1.25, в). пари сил, що виникає внаслідок дії сил опору підлоги, розподілених вздовж зануреного у підлогу кінця балки.
пари сил, що виникає внаслідок дії сил опору підлоги, розподілених вздовж зануреного у підлогу кінця балки.

 кН;
кН; кНм.
кНм. на шорстку стінку і підтримується у рівновазі за допомогою невагомого мотузка
на шорстку стінку і підтримується у рівновазі за допомогою невагомого мотузка  (рис. 1.24). Визначити коефіцієнт статичного тертя між стінкою і кінцем
(рис. 1.24). Визначити коефіцієнт статичного тертя між стінкою і кінцем  м,
м,  м, а найменший кут
м, а найменший кут  при рівновазі стержня дорівнює 45°.
при рівновазі стержня дорівнює 45°. і, звільняючи його від в’язей, реакції: натяг
і, звільняючи його від в’язей, реакції: натяг  мотузка в точці
мотузка в точці 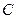 , напрямлений від
, напрямлений від  – нормальну реакцію і
– нормальну реакцію і 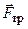 – статичну силу тертя ковзання. Сила тертя
– статичну силу тертя ковзання. Сила тертя 
 ,
, 
 , і з другого рівняння знаходимо
, і з другого рівняння знаходимо
 .
. знаходимо з третього рівняння.
знаходимо з третього рівняння. .
. , який утворює з вертикаллю
, який утворює з вертикаллю  кут 60° (рис. 1.25). Знайти реакції в’язей, якщо
кут 60° (рис. 1.25). Знайти реакції в’язей, якщо  м,
м,  м.
м. . Активною силою є вага полиці, яка прикладена у її геометричному центрі
. Активною силою є вага полиці, яка прикладена у її геометричному центрі  завіси, оскільки завіса не чинить опору пересуванню вздовж її осі. Отже, розкладаємо
завіси, оскільки завіса не чинить опору пересуванню вздовж її осі. Отже, розкладаємо  і
і  :
:  і
і  .
.

 Н;
Н;  Н;
Н;  Н;
Н; Н;
Н;  .
.


