
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення систем сил до найпростішого вигляду.Содержание книги
Поиск на нашем сайте
Інваріанти системи сил відносно центра зведення При зведенні системи сил до певного центра
а б Рисунок 1.35 Нехай кут між ними дорівнює Розкладаємо головний момент
Таким чином, вихідна система сил еквівалентна головному вектору Далі зауважимо, що сили У результаті первісна система сил звелася до головного вектора Цю сукупність сили і пари сил, яка лежить у площині, перпендикулярній до лінії дії сили, називають силовим гвинтом, або динамою. Пряму, яка проходить через точку Таким чином, доведено теорему: довільна система сил може бути зведена до силового гвинта. Розглянемо випадки так званого виродження силового гвинта. 1. Якщо
Таким чином, при є умовою зведення системи сил до рівнодійної, яку прикладено у точці Знайдемо момент рівнодійної
За означенням
Таким чином, на підставі (1.48) і (1.49)
Рівність (1.50) є узагальненням теореми Варіньйона для просторової системи сил: якщо система сил еквівалентна рівнодійній, то момент рівнодійної відносно центра Зрозуміло, що при 2. Якщо 3. Якщо Нарешті, з’ясуємо, чи впливає на елементи Припустимо, що спочатку Змінимо центр зведення і перенесемо Таким чином, при зміні центра зведення елементи
Рисунок 1.36
Центр паралельних сил і центр ваги У підрозділі 1.2.3 введено поняття центра паралельних сил Виведемо формулу, за якою можна знайти радіус-вектор Нехай для довільної системи паралельних сил (рис. 1.37) виконується умова
яка свідчить, що система сил зводиться до рівнодійної
Рисунок 1.37 Але ця сума дорівнює нулеві, оскільки точка
Розглянемо орт
і підставимо (1.53) в (1.52):
Дістанемо
Необхідна і достатня умова рівності нулеві векторного добутку (1.54) при будь-якому напрямі вектора
Звідси
Координати центра паралельних сил у прямокутній системі декартових координат з початком у точці
Далі розглянемо систему матеріальних точок, відстань між якими значно менша, ніж радіус земної кулі. При цьому сили ваги
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.148 (0.009 с.) |

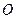 знаходи-мо її головний вектор
знаходи-мо її головний вектор 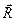 і головний момент
і головний момент 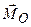 (рис. 1.35, а).
(рис. 1.35, а).
 . Зв’яжемо з
. Зв’яжемо з  і
і 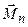 . Перша
. Перша 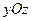 . Виберемо сили цієї пари рівними головному вектору
. Виберемо сили цієї пари рівними головному вектору 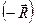 прикладаємо в центрі
прикладаємо в центрі 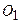 на відстані
на відстані 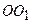 , яка є плечем
, яка є плечем  пари:
пари: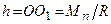 . (1.46)
. (1.46)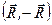 і певній парі сил, момент якої дорівнює
і певній парі сил, момент якої дорівнює 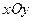 , тобто в площині, перпендикулярній до лінії дії
, тобто в площині, перпендикулярній до лінії дії 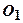 і паралельна лінії дії вектора
і паралельна лінії дії вектора  , називають центральною гвинтовою віссю.
, називають центральною гвинтовою віссю.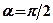 , то
, то 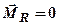 , тобто
, тобто  , і система сил зводиться до однієї сили
, і система сил зводиться до однієї сили  , тобто рівність нулеві їх скалярного добутку, має вигляд:
, тобто рівність нулеві їх скалярного добутку, має вигляд: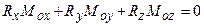 . (1.47)
. (1.47) і
і 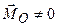 і
і  умова (1.47)
умова (1.47)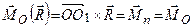 . (1.48)
. (1.48)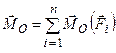 . (1.49)
. (1.49) . (1.50)
. (1.50)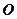 дорівнює векторній сумі моментів складових сил відносно того самого центра
дорівнює векторній сумі моментів складових сил відносно того самого центра  і
і  система сил також зводиться до рівнодійної.
система сил також зводиться до рівнодійної. ;
; 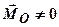 , то система сил зводиться до пари сил.
, то система сил зводиться до пари сил.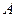 (рис. 1.36). Момент
(рис. 1.36). Момент 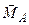 перпендикулярний до
перпендикулярний до 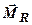 силового гвинта не змінюються. Тому їх називають інваріантами системи сил відносно центра зведення.
силового гвинта не змінюються. Тому їх називають інваріантами системи сил відносно центра зведення.
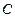 .
.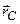 цієї точки.
цієї точки.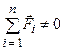 ,
, , на лінії дії якої знаходиться точка
, на лінії дії якої знаходиться точка 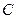 – центр паралельних сил. Проводимо
– центр паралельних сил. Проводимо 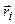 – радіус-вектор точки
– радіус-вектор точки  прикладання сили
прикладання сили 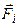 , а також
, а також  – радіус-вектор точки
– радіус-вектор точки 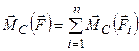 . (1.51)
. (1.51)
 ,
, 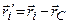 , з (1.51) маємо
, з (1.51) маємо . (1.52)
. (1.52)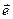 – одиничний вектор напряму системи паралельних сил. Кожну силу подамо у вигляді
– одиничний вектор напряму системи паралельних сил. Кожну силу подамо у вигляді (1.53)
(1.53) .
.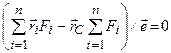 . (1.54)
. (1.54)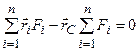 .
. . (1.55)
. (1.55)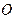 :
: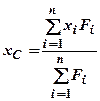 ;
;  ;
; 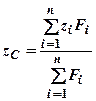 . (1.56)
. (1.56)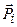 цих точок можна вважати паралельними силами.
цих точок можна вважати паралельними силами.


