
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механіка – це природнича наука, яка вивчає найпростіші рухи матерії – механічні.Содержание книги
Поиск на нашем сайте
Механіка – це природнича наука, яка вивчає найпростіші рухи матерії – механічні. Найпростіші форми рухів – це прості переходи фізичних тіл з одного положення у просторі і часі в інше, тому механіка є однією з природничих наук. Вивчаючи найзагальніші властивості рухів, механіка не враховує більшість конкретних властивостей фізичних тіл. Вона спирається лише на первісні властивості речовин; такі, як її протяжність і властивість частинок тяжіти одна до одної, тобто мати певну вагу. Зрозуміло, що в механіці користуються низкою спрощених (абстрактних) уявлень. В її основу покладено такі поняття, як матеріальна точка, система матеріальних точок та абсолютно тверде тіло. Поняття про матеріальну точку є однією з граничних абстракцій, яка виникла внаслідок спостережень за рухами тіл скінченних розмірів. Матеріальною точкою називають тіло, розмірами якого можна знехтувати при розв’язанні певних задач механіки. Системою матеріальних точок називають сукупність матеріальних точок, рухи й положення яких взаємопов’язані. Незмінною системою матеріальних точок називають систему, точки якої не змінюють взаємного положення протягом часу. Якщо точки суцільно заповнюють частину простору, який займає незмінна матеріальна система, то останню називають абсолютно твердим тілом. Основна властивість абсолютно твердого тіла полягає у незмінності відстані між будь-якими двома точками під час руху. Поняття про абсолютно тверде тіло є граничною абстракцією. Таким чином, Теоретичною механікою називають ту частину загальної механіки, яка вивчає рух матеріальних точок, систем матеріальних точок та абсолютно твердих тіл. Розглядаючи граничні абстракції, теоретична механіка вивчає найзагальніші закони механіки, які справедливі для всієї механіки. Теоретична механіка побудована за планом точних наук: в її основі лежить система означень та аксіом, на які, в свою чергу, спираються доведення теорем. РОЗДІЛ 1 ГЕОМЕТРИЧНА СТАТИКА Основні поняття та закони Рух матеріальної точки. Перший закон Ньютона. Основні властивості механічних сил Основні поняття класичної механіки вперше були сформульовані І. Ньютоном, який розглядав рух вільної матеріальної точки, тобто такої, на рух якої заздалегідь не накладені будь-які обмеження, які не залежать від подальшого закону руху. Перший закон І. Ньютона (закон інерції) стверджує, що ізольована матеріальна точка зберігає стан рівномірного і прямолінійного руху або перебуває у стані спокою відносно системи координат, яка рухається поступально, рівномірно і прямолінійно. Вважається, що ця система координат рухається відносно нерухомої системи координат. Наявність абсолютно нерухомої системи координат є однією з основ, на якій ґрунтується класична механіка. Якщо рух точки відрізняється від рівномірного і прямолінійного, то це означає, що на точку діють будь-які зовнішні фактори. Причину, внаслідок якої матеріальна точка змінює свій рух, називають механічною силою. Переважна більшість рухів точок на Землі відрізняється від рівномірного й прямолінійного. Тому поняття ізольованої матеріальної точки є граничною абстракцією. Точки матеріальної системи завжди перебувають під взаємним впливом. Якщо будь-який рух переноситься з одного тіла на інше, то він активний і його можна розглядати як причину руху. Отже, механічна сила є рух, який у механічній формі передається від одного тіла до іншого при їхній взаємодії. Кожна сила має величину, напрям у просторі і точку прикладання. Поняття механічної сили стійко прижилося в процесі еволюції науки, оскільки механічну силу можна кількісно виміряти й записати як функцію часу, координат точок простору та їхніх похідних за часом, тобто знайти її аналітичне визначення. Сили зображають напрямленими відрізками прямих. Пряму, вздовж якої відкладають відрізок, що зображає силу, називають лінією дії сили. Сформулюємо основні означення та аксіоми щодо механічних сил. Означення 1. Зрівноваженою системою сил, або системою, еквівалентною нулеві, називають таку, під дією якої точка рухається рівномірно і прямолінійно або перебуває у стані спокою. Означення 2. Матеріальна точка знаходиться у стані статичної рівноваги, якщо вона перебуває під дією зрівноваженої системи сил. Означення 3. Матеріальна система знаходиться у стані статичної рівноваги, якщо кожна її точка перебуває у стані рівноваги. Відповідно до цих означень зауважимо, що рух матеріальної системи не зміниться, якщо до її точок прикладати або від неї віднімати зрівноважену систему сил. Означення 4. Дві системи сил називають статично еквівалентними, якщо кожна з них окремо зрівноважує одну й ту саму третю систему сил. Означення 5. Рівнодійною системи сил називають силу, еквівалентну системі сил. Силу, що зрівноважує систему сил, називають зрівноважуючою. І. Ньютон у додаткових зауваженнях до основних законів механіки аксіоматично сформулював правило паралелограма сил, яке дістало назву аксіоми про паралелограм сил. Означення статики Поставимо за мету встановити властивості систем сил, прикладених до абсолютно твердих тіл. Такі властивості вивчає окремий розділ механіки, який дістав назву статики. Зауважимо, що ми не розглядаємо властивостей рухів, які спричиняються цими силами. Статика вивчає перетворення системи сил, прикладених до твердих тіл. Внаслідок цього перетворення вихідна система сил замінюється іншою, статично еквівалентною першій. Статика вивчає також умови рівноваги тіл, які перебувають під дією певної системи сил. Отже, статика вивчає умови рівноваги систем сил як окремий випадок перетворення цих систем.
Механічні в’язі та їхні реакції
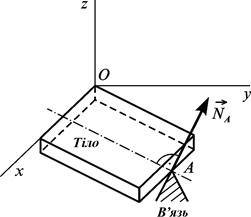
Розглянемо систему матеріальних точок. Якщо їхні рухи заздалегідь нічим не обмежені, то систему називають вільною. Якщо існують заздалегідь означені геометричні або кінематичні обмеження рухів точок системи, то її називають невільною. Наприклад, кожний механізм, рух точок якого геометрично обмежений, є невільною системою. В’язь – гладенька поверхня
Гостре вістря або ребро У тому випадку, коли об’єкт спирається на гостре вістря або ребро двогранного кута, реакція в’язі
Для розглянутих випадків можна сформулювати загальне правило: В’язь – шорстка поверхня
Напрям реакції
В’язь – стержень
Вважають, що стержень тонкий невагомий із точковими шарнірами на кінцях. Такий стержень перешкоджає переміщенню точки В об’єкта у напрямі прямої, що проходить через точкові шарніри А і В. Значить і реакція
На відміну від нитки, яка повинна бути завжди натягнута, стержень може бути як розтягнутим, так і стиснутим. Це означає, що заздалегідь можна вказати лише лінію дії реакції стержня Якщо стержень має вагу, то характер обмежень, що він накладає на рух точки В об’єкта, буде складнішим. Такий стержень варто розглядати як самостійний об’єкт, для якого точкові шарніри є в’язями.
Сферичний шарнір
Підп’ятник Рисунок 1.3 Проведемо переріз через шарнір
1.1.6. Теорема про рівновагу трьох непаралельних сил, Теорема. Якщо тверде тіло перебуває у рівновазі під дією трьох непаралельних сил, дві з яких лежать в одній площині, то лінії дії всіх трьох сил перетинаються в одній точці, а трикутник цих сил замкнений. t Нехай тіло (рис. 1.4) перебуває під дією трьох непара-
Рисунок 1.4 Застосування цієї теореми покажемо на прикладі. Приклад 1.1. Визначити реакції опор невагомого стержня Розв’язання. Розглянемо стержень AD, який перебуває в рівновазі під дією сили Реакція
Рисунок 1.5 Знайшовши довжини сторін трикутника
Тертя ковзання (тертя першого роду) виникає, коли відносна швидкість точок тіл, що перебувають у контакті, не дорівнює нулеві. Тертя кочення (тертя другого роду) виникає при коченні без ковзання. У цьому разі відносна швидкість точок контакту дорівнює нулеві. Розрізняють ще тертя вертіння (тертя третього роду). Розглянемо лише тертя першого роду, основні властивості якого відкрив відомий фізик Кулон. Якщо одне тіло не рухається по поверхні іншого, то виникає сила тертя спокою, яка має неозначений напрям і величину. Але оскільки сила тертя – гальмуюча сила, то домовились вважати, що сила тертя спокою напрямлена протилежно напряму того руху, який почне здійснюватись, коли тіло вийде зі стану спокою під дією активних сил. При взаємному русі тіл виникає сила тертя руху. Вона майже не залежить від величини відносної швидкості між тілами. Рисунок 1.6 Нормальна складова Якщо позначити через
Згідно (1.2), якщо
то тіло перебуває в стані рівноваги. Вираз (1.4) може набути вигляду
Якщо позначити через
Кут Обертаючи Якщо лінія дії сили
Тіло рухається якщо Зауважимо, що ці висновки не залежать від величини сили Розглянемо рівновагу важкої матеріальної точки на похилій шорсткій площині (рис. 1.7), яка утворює кут Точка знаходиться у стані граничної рівноваги, якщо
Звідси
або
Граничне значення кута Доцільно розглянути ще один випадок урахування сили тертя в деяких механізмах. Уявімо собі, що треба підняти певний тягар В стані рівноваги при відсутності тертя натяг
де
1.2. Основні властивості систем сил, Рисунок 1.12 Оскільки вектори
Якщо в (1.9) підставити значення вектора
звідки
Це свідчить про те, що векторний добуток На підставі цього твердження вважаємо вираз Цей вираз, який позначається
Вважаємо вектор
Введемо особливе позначення вектора сили, прикладеного до твердого тіла. Цей вектор аналітично визначається трьома компонентами (проекціями) сили і трьома проекціями вектора
Серед указаних шести компонент вектора Модуль вектора
Тут і надалі позначатимемо модулі векторів так, як і вектори, але без стрілок над літерами. Величину
тобто модуль моменту дорівнює добутку сили на плече. У правій системі координат вектор Момент Проекції вектора
де У лівих частинах і перших доданках правих частин виразів (1.15) індекси
Зосередимо увагу на одному з виразів (1.15), наприклад, на проекції
До його правої частини не входить координата Тому проекції
Рисунок 1.13 Розглянемо проекцію
Порівнюючи (1.16) і (1.17), доходимо висновку, що моменти цих двох сил відносно осі На підставі цього формулюємо робоче правило обчислення моменту сили відносно осі: Рисунок 1.14
Умова рівноваги (1.20) є як необхідною, так і достатньою, бо з неї випливає рівність нулеві обох компонент ковзного вектора Умову (1.20) називають ще механічною, або фізичною, умовою рівноваги збіжної системи сил. Очевидно, що багатокутник сил за (1.20) замкнений. У цьому полягає геометрична (графічна) умова рівноваги. На підставі (1.18) проекції рівнодійної сили на осі прямокутної декартової системи координат дорівнюють алгебраїчним сумам проекцій складових сил на осі координат
Отже, згідно з механічною умовою рівноваги (1.20) на підставі (1.21) дістаємо аналітичні умови рівноваги збіжної системи сил:
Рисунок 1.15 Початок системи координат виберемо в точці О, додатні напрями осей позначено на рис. 1.15. 3. Складаємо рівняння рівноваги:
На підставі першого рівняння робимо висновок, що
Від’ємний знак свідчить, що цей стержень стиснутий, оскільки спочатку припускали, що він розтягнутий. Нарешті, з третього рівняння знайдемо
Додатний знак цих реакцій вказує, що стержні АВ і АС розтягнуті.
1.2.3. Аналітичне визначення ковзного вектора Розглянемо дві паралельні сили Покажемо, що така система сил зводиться до рівнодійної. З’єднаємо точки Первісна система сил
Рисунок 1.19 Таким чином, система паралельних сил
Згідно з означенням (§ 1.1.1) запишемо вираз моменту рівнодійної
Оскільки радіус-вектор
то вираз (1.24) набуває вигляду
Отже,
Цей результат справджується також для сил, які мають однакові напрями. Для системи паралельних сил
Рисунок 1.20 Точку Можна легко переконатися, що точка Отже, Рисунок 1.21 Кожна сила
Векторну суму моментів приєднаних пар сил називають головним моментом
У системі декартових прямокутних координат з початком у центрі зведення
де Знаючи компоненти
а його напрямні косинуси відповідно рівні:
Приклади Приклад 1.3. На балку Розв’язання. 1. Як згадувалося раніше, спочатку треба виділити тіло, рівновагу якого розглядаємо. Таким тілом є балка 2. Аналізуємо сили. На балку діють сили

б Рисунок 1.22
На балку діє довільна система сил, розміщена на площині 3. Складемо рівняння рівноваги у вигляді (1.41):
У третьому рівнянні центр моментів взято у точці 4. Розв’язуючи систему рівнянь рівноваги, дістанемо
5. Аналізуючи розв’язок задачі (здобуті значення
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.016 с.) |


 буде спрямована по цій нормалі в бік тіла.
буде спрямована по цій нормалі в бік тіла.
 буде спрямована по нормалі до поверхні об’єкта в бік тіла.
буде спрямована по нормалі до поверхні об’єкта в бік тіла.





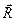 наперед невідомий, тому її розкладають на дві складові: нормальну реакцію опори
наперед невідомий, тому її розкладають на дві складові: нормальну реакцію опори  і дотичну – силу тертя
і дотичну – силу тертя 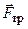 .
. (зусилля) стержня прикладена в точці В і спрямована вздовж прямої АВ до точки А або від неї.
(зусилля) стержня прикладена в точці В і спрямована вздовж прямої АВ до точки А або від неї.
 Будь-які за конструкцією тверді невагомі в’язі з двома зовнішніми точковими шарнірами на кінцях можна розглядати як стержні, напрям реакцій яких проходить через точкові шарніри А і В. Тому і реакція
Будь-які за конструкцією тверді невагомі в’язі з двома зовнішніми точковими шарнірами на кінцях можна розглядати як стержні, напрям реакцій яких проходить через точкові шарніри А і В. Тому і реакція 

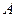 і розглядатимемо, наприклад, тіло АС як в’язь відносно тіла
і розглядатимемо, наприклад, тіло АС як в’язь відносно тіла  . Застосовуючи аксіому про звільнення від в’язей, прикладемо в точці
. Застосовуючи аксіому про звільнення від в’язей, прикладемо в точці  відкинутого тіла
відкинутого тіла  . Вона буде зовнішньою силою відносно тіла
. Вона буде зовнішньою силою відносно тіла  ,
,  ,
,  , причому сили
, причому сили  . Тверде тіло тепер перебуває в рівновазі під дією двох сил
. Тверде тіло тепер перебуває в рівновазі під дією двох сил  і
і  , тобто трикутник сил замкнений u.
, тобто трикутник сил замкнений u.
 , який перебуває в рівновазі під дією активної сили
, який перебуває в рівновазі під дією активної сили 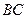 і нерухомої опори
і нерухомої опори  , прикладемо реакції в’язей (рис. 1.5, б).
, прикладемо реакції в’язей (рис. 1.5, б).  і
і  відповідно.
відповідно. перетину ліній дії сил
перетину ліній дії сил 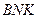 (
( проведено паралельно лінії дії
проведено паралельно лінії дії  .
. а
а
 б
б
 в
в
 ;
;  .
. спричиняє стиск між тілом і поверхнею і викликає нормальну реакцію поверхні. Позначимо її через
спричиняє стиск між тілом і поверхнею і викликає нормальну реакцію поверхні. Позначимо її через 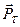 може викликати рух тіла у напрямі дотичної в тому разі, коли вона буде більшою за граничну силу тертя спокою.
може викликати рух тіла у напрямі дотичної в тому разі, коли вона буде більшою за граничну силу тертя спокою. кут між силою
кут між силою  і нормаллю до поверхні, то модулі
і нормаллю до поверхні, то модулі .
. , (1.4)
, (1.4)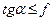 . (1.5)
. (1.5) гострий кут між реакцією
гострий кут між реакцією  . (1.6)
. (1.6) знаходиться всередині конуса тертя, то тіло перебуває в стані рівноваги, оскільки виконується нерівність (1.5):
знаходиться всередині конуса тертя, то тіло перебуває в стані рівноваги, оскільки виконується нерівність (1.5): ;
;  .
. .
. . Точка перебуває також під дією сили
. Точка перебуває також під дією сили  .
.
 . (1.7)
. (1.7) мотузка дорівнював би силі ваги тягаря. Але сила тертя збільшує натяг. Знайти цю силу можна за допомогою формули Ейлера
мотузка дорівнював би силі ваги тягаря. Але сила тертя збільшує натяг. Знайти цю силу можна за допомогою формули Ейлера , (1.8)
, (1.8) Рисунок 1.7
Рисунок 1.7
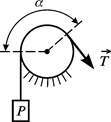 Рисунок 1.8
Рисунок 1.8
 і
і  *. (1.9)
*. (1.9)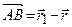 , що очевидно з рис. 1.12, то маємо рівність
, що очевидно з рис. 1.12, то маємо рівність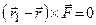 ,
, . (1.10)
. (1.10) не залежить від положення точки
не залежить від положення точки  , називають моментом сили
, називають моментом сили 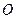 . Отже,
. Отже, . (1.11)
. (1.11)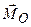 і
і 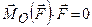 . (1.12)
. (1.12) . (1.13)
. (1.13)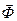 тільки п’ять незалежні відповідно до (1.12).
тільки п’ять незалежні відповідно до (1.12). .
. – найкоротшу відстань від точки
– найкоротшу відстань від точки 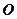 до лінії дії сили називають плечем сили відносно точки О. Отже,
до лінії дії сили називають плечем сили відносно точки О. Отже,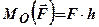 , (1.14)
, (1.14) напрямлений у бік спостерігача, який бачить, що сила
напрямлений у бік спостерігача, який бачить, що сила  намага-ється повернути тіло навколо точки
намага-ється повернути тіло навколо точки  вважаємо додатною.
вважаємо додатною.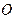 у напрямі руху годинникової стрілки
у напрямі руху годинникової стрілки ;
; ; (1.15)
; (1.15) ,
,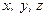 – проекції радіуса-вектора
– проекції радіуса-вектора  (початок координат вибрано у точці
(початок координат вибрано у точці  – проекції вектора сили
– проекції вектора сили 
 :
: . (1.16)
. (1.16) точки А прикладання сил
точки А прикладання сил  ,
,  ,
,  називають моментами сили
називають моментами сили  ,
,  ,
, 
 і вважатимемо її вектором. Знайдемо моменти
і вважатимемо її вектором. Знайдемо моменти  ,
,  ,
,  . (1.17)
. (1.17)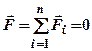 . (1.20)
. (1.20) ;
;  ;
;  . (1.21)
. (1.21) ;
;  ;
;  . (1.22)
. (1.22)


 , з другого рівняння знаходимо
, з другого рівняння знаходимо  :
: .
.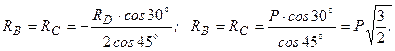
 і
і  прикладання сил
прикладання сил 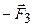 , лінії дії яких збігаються з відрізком
, лінії дії яких збігаються з відрізком  , а модулі довільні. Згідно з означеннями 1-3 § 1.1.1 рух тіла при цьому не зміниться.
, а модулі довільні. Згідно з означеннями 1-3 § 1.1.1 рух тіла при цьому не зміниться. і
і  , які вже не є паралельними. Їхні лінії дії перетинаються у певній точці
, які вже не є паралельними. Їхні лінії дії перетинаються у певній точці  .
.
 . (1.23)
. (1.23) . (1.24)
. (1.24) дорівнює сумі двох векторів:
дорівнює сумі двох векторів: , (1.25)
, (1.25) .(1.26)
.(1.26) . (1.27)
. (1.27)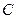 перетину її лінії дії з продовженням відрізка
перетину її лінії дії з продовженням відрізка 
 називають центром паралельних сил
називають центром паралельних сил  і
і  .
.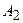 . Легко також зрозуміти, що поняття центра паралельних сил можна поширити на три, чотири і більше паралельних сил.
. Легко також зрозуміти, що поняття центра паралельних сил можна поширити на три, чотири і більше паралельних сил. з відповідною
з відповідною  , яка прикладена в центрі
, яка прикладена в центрі  , яку називають приєднаною парою. Крім того, є ще система сил
, яку називають приєднаною парою. Крім того, є ще система сил  , прикладена в точці
, прикладена в точці  системи сил:
системи сил: . (1.34)
. (1.34) відносно центра зведення О:
відносно центра зведення О: . (1.35)
. (1.35) ;
;  ;
;  . (1.36)
. (1.36) ;
; ; (1.37)
; (1.37) ,
, – проекції сили
– проекції сили  – координати точки прикладання сили
– координати точки прикладання сили  і
і  , завжди можна знайти модулі та напрямні косинуси відповідно векторів
, завжди можна знайти модулі та напрямні косинуси відповідно векторів  ,
, ;
;  ;
;  .
. Н,
Н,  Н і пара сил з моментом
Н і пара сил з моментом  Н×м (рис. 1.22). Нехтуючи вагою балки і тертям, знайти реакції опор.
Н×м (рис. 1.22). Нехтуючи вагою балки і тертям, знайти реакції опор. і
і  і пара сил з моментом
і пара сил з моментом  На підставі аксіоми про звільнення від в’язей, відкинемо всі в’язі – нерухому
На підставі аксіоми про звільнення від в’язей, відкинемо всі в’язі – нерухому  .
. , до складу якої входять три невідомі сили (скалярні величини):
, до складу якої входять три невідомі сили (скалярні величини):  . Для такої системи можна скласти три рівняння рівноваги. Отже, задача статично визначена.
. Для такої системи можна скласти три рівняння рівноваги. Отже, задача статично визначена.
 і
і  відносно точки
відносно точки  .
.
 і
і  ), зауважимо, що всі в
), зауважимо, що всі в 


