Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Якщо на матеріальну точку діють дві сили, то їхню дію можна замінити дією однієї сили – їм рівнодійної, яка визначається діагоналлю паралелограма, побудованого на цих силах.Содержание книги
Поиск на нашем сайте
Ця аксіома формулює правило векторного додавання сил. Відтепер можна вважати механічні сили векторами. У механіці розглядають вектори трьох типів: означені, або прикладені, ковзні та вільні. Означений вектор, наприклад, вектор сили, що діє на точку, характеризується трьома його проекціями Ковзний вектор можна переносити вздовж лінії його дії. Тому він визначається п’ятьма параметрами, оскільки три координати точки прикладання вектора зв’язані системою двох рівнянь, які визначають лінію дії вектора у просторі. Нарешті, для визначення вільного вектора потрібно знати лише три його проекції. Аксіома про абсолютно тверде тіло. Якщо тверде тіло перебуває у рівновазі під дією двох сил, то ці сили протилежні за напрямом, однакові за величиною і мають спільну лінію дії. Зрівноважену систему сил Теорема. Стан механічного руху тіла не зміниться, якщо силу перемістити вздовж лінії її дії у будь-яку точку. t* Нехай на тіло (рис. 1.2) діє сила
Отже, на підставі доведеної теореми, вектор сили, прикладеної до абсолютно твердого тіла, можна вважати Означення статики Поставимо за мету встановити властивості систем сил, прикладених до абсолютно твердих тіл. Такі властивості вивчає окремий розділ механіки, який дістав назву статики. Зауважимо, що ми не розглядаємо властивостей рухів, які спричиняються цими силами. Статика вивчає перетворення системи сил, прикладених до твердих тіл. Внаслідок цього перетворення вихідна система сил замінюється іншою, статично еквівалентною першій. Статика вивчає також умови рівноваги тіл, які перебувають під дією певної системи сил. Отже, статика вивчає умови рівноваги систем сил як окремий випадок перетворення цих систем.
Механічні в’язі та їхні реакції
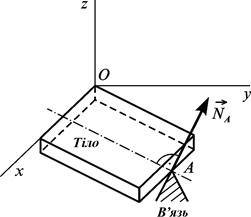
Розглянемо систему матеріальних точок. Якщо їхні рухи заздалегідь нічим не обмежені, то систему називають вільною. Якщо існують заздалегідь означені геометричні або кінематичні обмеження рухів точок системи, то її називають невільною. Наприклад, кожний механізм, рух точок якого геометрично обмежений, є невільною системою. Тіла, які обмежують рухи точок матеріальної системи, називають в’язями. Зауважимо, що тут йдеться лише про так звані фізичні в’язі. Наявність в’язей змінює рух системи матеріальних точок. Вони відхиляють систему від рухів вільної системи, тобто в’язі є матеріальні джерела певних сил Реакціями в’язей називають сили, що діють з боку в’язей на систему, рух якої вивчаємо. Часто рух певного твердого тіла обмежений наявністю якогось іншого тіла. Це обмеження зумовлено властивістю матерії (речовини), яку називають непроникністю. Тому реакція Розглянемо деякі приклади фізичних в’язей та їхні реакції. При визначенні напряму реакцій в’язей будемо виходити з наступних положень: по-перше, реакція кожної в’язі повинна бути прикладена до об’єкта в точці, у якій ця в’язь контактує з ним і виключає які-небудь переміщення; по-друге, реакція в’язі повинна бути спрямована в бік протилежний тому напряму, по якому в’язь перешкоджає переміщенню з розглянутого положення згаданої вище точки об’єкта. В’язь – гладенька поверхня
Гостре вістря або ребро У тому випадку, коли об’єкт спирається на гостре вістря або ребро двогранного кута, реакція в’язі
Для розглянутих випадків можна сформулювати загальне правило:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.005 с.) |

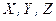 на всі осі координат і координатами
на всі осі координат і координатами 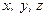 точки його прикладання, тобто шістьма параметрами.
точки його прикладання, тобто шістьма параметрами. і
і 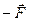 , яка діє на абсолютно тверде тіло, зображено на рис. 1.1.
, яка діє на абсолютно тверде тіло, зображено на рис. 1.1.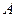 . Стан механічного руху тіла не зміниться, якщо в довільній точці
. Стан механічного руху тіла не зміниться, якщо в довільній точці  , розташованій на лінії дії сили
, розташованій на лінії дії сили  ). На підставі попередніх означень та аксіоми про абсолютно тверде тіло можна вважати силу
). На підставі попередніх означень та аксіоми про абсолютно тверде тіло можна вважати силу  Рисунок 1.1
Рисунок 1.1
 Рисунок 1.2
Рисунок 1.2
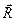 (реакцій в’язей), які прикладені до точок або тіл, що входять до системи.
(реакцій в’язей), які прикладені до точок або тіл, що входять до системи.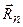 і дотичну
і дотичну  до поверхонь в’язі та тіла, то
до поверхонь в’язі та тіла, то 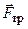 .
.
 буде спрямована по цій нормалі в бік тіла.
буде спрямована по цій нормалі в бік тіла.
 буде спрямована по нормалі до поверхні об’єкта в бік тіла.
буде спрямована по нормалі до поверхні об’єкта в бік тіла.