
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила тертя спокою завжди більша за силу тертя руху.Содержание книги
Поиск на нашем сайте
Основний кількісний закон тертя ковзання полягає в тому, що гранична величина сили статичного тертя пропорційна силі нормального стиску між поверхнями тіл:
де Сила тертя спокою задовольняє нерівність
де знак рівності відповідає станові граничної рівноваги між силою тертя й активними силами. Сила тертя руху
де Сила тертя руху напрямлена у бік, протилежний відносній швидкості. Коефіцієнт тертя знаходять експериментально. Кут тертя, конус тертя, кут природного укосу. Нехай певне тіло А лежить у горизонтальній площині (рис. 1.6), на тіло діє сила
Рисунок 1.6 Нормальна складова Якщо позначити через
Згідно (1.2), якщо
то тіло перебуває в стані рівноваги. Вираз (1.4) може набути вигляду
Якщо позначити через
Кут Обертаючи Якщо лінія дії сили
Тіло рухається якщо Зауважимо, що ці висновки не залежать від величини сили Розглянемо рівновагу важкої матеріальної точки на похилій шорсткій площині (рис. 1.7), яка утворює кут Точка знаходиться у стані граничної рівноваги, якщо
Звідси
або
Граничне значення кута Доцільно розглянути ще один випадок урахування сили тертя в деяких механізмах. Уявімо собі, що треба підняти певний тягар В стані рівноваги при відсутності тертя натяг
де
1.2. Основні властивості систем сил, Аналітичне визначення ковзного вектора. Момент сили відносно точки і осі Розглянемо ковзний вектор сили
Рисунок 1.12 Оскільки вектори
Якщо в (1.9) підставити значення вектора
звідки
Це свідчить про те, що векторний добуток На підставі цього твердження вважаємо вираз Цей вираз, який позначається
Вважаємо вектор
Введемо особливе позначення вектора сили, прикладеного до твердого тіла. Цей вектор аналітично визначається трьома компонентами (проекціями) сили і трьома проекціями вектора
Серед указаних шести компонент вектора Модуль вектора
Тут і надалі позначатимемо модулі векторів так, як і вектори, але без стрілок над літерами. Величину
тобто модуль моменту дорівнює добутку сили на плече. У правій системі координат вектор Момент Проекції вектора
де У лівих частинах і перших доданках правих частин виразів (1.15) індекси
Зосередимо увагу на одному з виразів (1.15), наприклад, на проекції
До його правої частини не входить координата Тому проекції
Рисунок 1.13 Розглянемо проекцію
Порівнюючи (1.16) і (1.17), доходимо висновку, що моменти цих двох сил відносно осі На підставі цього формулюємо робоче правило обчислення моменту сили відносно осі:
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.95.167 (0.01 с.) |

 , (1.1)
, (1.1) – гранична величина сили тертя спокою;
– гранична величина сили тертя спокою;  – сила нормального стиску поверхонь тіл;
– сила нормального стиску поверхонь тіл;  – коефіцієнт пропорційності, який називають коефіцієнтом статичного тертя ковзання.
– коефіцієнт пропорційності, який називають коефіцієнтом статичного тертя ковзання. , (1.2)
, (1.2) ,
,  , (1.3)
, (1.3) – коефіцієнт тертя руху.
– коефіцієнт тертя руху. . Розкладемо її на нормальну
. Розкладемо її на нормальну  і дотичну
і дотичну 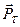 складові до поверхні.
складові до поверхні.
 . Дотична складова
. Дотична складова  кут між силою
кут між силою  .
. , (1.4)
, (1.4)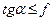 . (1.5)
. (1.5) гострий кут між реакцією
гострий кут між реакцією 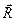 площини і нормаллю до її поверхні у стані граничної рівноваги, то на підставі (1.1)
площини і нормаллю до її поверхні у стані граничної рівноваги, то на підставі (1.1) . (1.6)
. (1.6) знаходиться всередині конуса тертя, то тіло перебуває в стані рівноваги, оскільки виконується нерівність (1.5):
знаходиться всередині конуса тертя, то тіло перебуває в стані рівноваги, оскільки виконується нерівність (1.5): ;
;  .
. .
. . Точка перебуває також під дією сили
. Точка перебуває також під дією сили 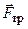 .
. .
.
 . (1.7)
. (1.7) мотузка дорівнював би силі ваги тягаря. Але сила тертя збільшує натяг. Знайти цю силу можна за допомогою формули Ейлера
мотузка дорівнював би силі ваги тягаря. Але сила тертя збільшує натяг. Знайти цю силу можна за допомогою формули Ейлера , (1.8)
, (1.8) Рисунок 1.7
Рисунок 1.7
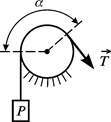 Рисунок 1.8
Рисунок 1.8
 , прикладений до абсолютно твердого тіла (рис. 1.12) у довільній точці
, прикладений до абсолютно твердого тіла (рис. 1.12) у довільній точці 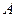 . Проведемо з певного центра
. Проведемо з певного центра 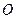 радіус-вектор
радіус-вектор  точки А. Візьмемо на лінії дії сили
точки А. Візьмемо на лінії дії сили  з того самого центра
з того самого центра 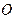 .
.
 і
і  *. (1.9)
*. (1.9)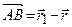 , що очевидно з рис. 1.12, то маємо рівність
, що очевидно з рис. 1.12, то маємо рівність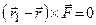 ,
, . (1.10)
. (1.10) не залежить від положення точки
не залежить від положення точки  , називають моментом сили
, називають моментом сили  . (1.11)
. (1.11)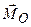 і
і 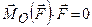 . (1.12)
. (1.12) . (1.13)
. (1.13)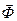 тільки п’ять незалежні відповідно до (1.12).
тільки п’ять незалежні відповідно до (1.12). .
. – найкоротшу відстань від точки
– найкоротшу відстань від точки 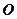 до лінії дії сили називають плечем сили відносно точки О. Отже,
до лінії дії сили називають плечем сили відносно точки О. Отже,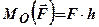 , (1.14)
, (1.14) напрямлений у бік спостерігача, який бачить, що сила
напрямлений у бік спостерігача, який бачить, що сила  намага-ється повернути тіло навколо точки
намага-ється повернути тіло навколо точки  вважаємо додатною.
вважаємо додатною. ;
; ; (1.15)
; (1.15) ,
,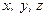 – проекції радіуса-вектора
– проекції радіуса-вектора  – проекції вектора сили
– проекції вектора сили 
 :
: . (1.16)
. (1.16) точки А прикладання сил
точки А прикладання сил  ,
,  ,
,  називають моментами сили
називають моментами сили  ,
,  ,
, 
 сили
сили  і вважатимемо її вектором. Знайдемо моменти
і вважатимемо її вектором. Знайдемо моменти  ,
,  ,
,  . (1.17)
. (1.17)


