
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Щоб обчислити момент сили відносно осі, треба спроектувати силу на площину, яка перпендикулярна до осі, і, розглядаючи проекцію як вектор, знайти її момент відносно точки перетину осі та площини.Содержание книги
Поиск на нашем сайте
Момент сили відносно осі додатний, якщо, спостерігаючи з додатного напряму осі, бачимо, що сила намагається повернути тіло навколо осі проти руху годинникової стрілки. Якщо напрям обертання тіла збігається з напрямом руху годинникової стрілки, то момент сили від’ємний. Перпендикуляр З формулювання робочого правила випливає, що момент сили відносно осі дорівнює нулеві, якщо сила і вісь лежать в одній площині.
Система збіжних сил. Умови рівноваги Систему сил називають збіжною, якщо лінії дії сил перетинаються в одній точці (рис. 1.14). Згідно з аксіомою про паралелограм сил рівнодійна цієї системи сил дорівнює геометричній сумі складових сил
Щоб дати аналітичне визначення ковзного вектора рівнодійної, треба знайти її момент відносно довільної точки
Згідно з (1.19) Момент рівнодійної відносно довільного центра дорівнює геометричній (векторній) сумі моментів складових сил відносно того самого центра. Наведене твердження є змістом теореми Варіньйона щодо збіжної системи сил. Умовою рівноваги збіжної системи сил є рівність нулеві їх рівнодійної:
Рисунок 1.14
Умова рівноваги (1.20) є як необхідною, так і достатньою, бо з неї випливає рівність нулеві обох компонент ковзного вектора Умову (1.20) називають ще механічною, або фізичною, умовою рівноваги збіжної системи сил. Очевидно, що багатокутник сил за (1.20) замкнений. У цьому полягає геометрична (графічна) умова рівноваги. На підставі (1.18) проекції рівнодійної сили на осі прямокутної декартової системи координат дорівнюють алгебраїчним сумам проекцій складових сил на осі координат
Отже, згідно з механічною умовою рівноваги (1.20) на підставі (1.21) дістаємо аналітичні умови рівноваги збіжної системи сил:
Рівності (1.22) називають аналітичними рівняннями рівноваги. У разі потреби з них можна знайти не більш як три алгебраїчних невідомих. Якщо кількість невідомих перевищує кількість рівнянь рівноваги, задачу називають статично невизначеною. Розглянемо приклад застосування рівнянь рівноваги, на якому проілюструємо методику розв’язування задач статики. Приклад 1.2. Три невагомих стержні Розв’язання. 1. Виділимо тіло або точку, умови рівноваги якої дадуть можливість розв’язати задачу. Це – точка 2. Аналізуємо сили, які прикладені до вузла А. На вузол А діє активна сила
Рисунок 1.15 Початок системи координат виберемо в точці О, додатні напрями осей позначено на рис. 1.15. 3. Складаємо рівняння рівноваги:
На підставі першого рівняння робимо висновок, що
Від’ємний знак свідчить, що цей стержень стиснутий, оскільки спочатку припускали, що він розтягнутий. Нарешті, з третього рівняння знайдемо
Додатний знак цих реакцій вказує, що стержні АВ і АС розтягнуті.
1.2.3. Аналітичне визначення ковзного вектора Розглянемо дві паралельні сили Покажемо, що така система сил зводиться до рівнодійної. З’єднаємо точки Первісна система сил
Рисунок 1.19 Таким чином, система паралельних сил
Згідно з означенням (§ 1.1.1) запишемо вираз моменту рівнодійної
Оскільки радіус-вектор
то вираз (1.24) набуває вигляду
Отже,
Цей результат справджується також для сил, які мають однакові напрями. Для системи паралельних сил
Рисунок 1.20 Точку Можна легко переконатися, що точка Отже,
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.195.82 (0.008 с.) |

 , проведений з точки
, проведений з точки 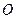 до лінії дії сиди
до лінії дії сиди  , називатимемо плечем сили
, називатимемо плечем сили  відносно осі
відносно осі  .
. . (1.18)
. (1.18)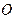 :
: . (1.19)
. (1.19)
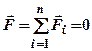 . (1.20)
. (1.20)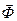 (1.13).
(1.13). ;
;  ;
;  . (1.21)
. (1.21) ;
;  ;
;  . (1.22)
. (1.22) ,
,  і
і  закріплені шарнірно в точці
закріплені шарнірно в точці 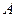 і за допомогою шарнірів
і за допомогою шарнірів  ,
, 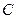 ,
,  прикріплені до горизонтальної підставки (рис. 1.15). Площини трикутників
прикріплені до горизонтальної підставки (рис. 1.15). Площини трикутників  і
і 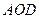 вертикальні і взаємно перпен-дикулярні. На вузол
вертикальні і взаємно перпен-дикулярні. На вузол  діє сила
діє сила  кН. Знайти зусилля в стержнях, якщо
кН. Знайти зусилля в стержнях, якщо  ;
;  .
. , до якої збігаються всі стержні, зусилля в яких треба визначити. Отже, розглянемо рівновагу вузла
, до якої збігаються всі стержні, зусилля в яких треба визначити. Отже, розглянемо рівновагу вузла  , а також три реакції стержнів, які діють вздовж них, оскільки стержні ідеальні. Припустимо, що всі стержні розтягнуті, тому на рис. 1.15 їхні реакції напрямлені від вузла А. В задачі три невідомі
, а також три реакції стержнів, які діють вздовж них, оскільки стержні ідеальні. Припустимо, що всі стержні розтягнуті, тому на рис. 1.15 їхні реакції напрямлені від вузла А. В задачі три невідомі  , для відшукання яких можна скласти три рівняння рівноваги. Таким чином, задача статично визначена.
, для відшукання яких можна скласти три рівняння рівноваги. Таким чином, задача статично визначена.



 , з другого рівняння знаходимо
, з другого рівняння знаходимо  :
: .
.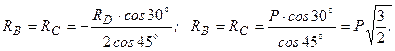
 , різні за модулем і протилежні за напрямом (рис. 1.19).
, різні за модулем і протилежні за напрямом (рис. 1.19). і
і  прикладання сил
прикладання сил  і
і 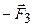 , лінії дії яких збігаються з відрізком
, лінії дії яких збігаються з відрізком  , а модулі довільні. Згідно з означеннями 1-3 § 1.1.1 рух тіла при цьому не зміниться.
, а модулі довільні. Згідно з означеннями 1-3 § 1.1.1 рух тіла при цьому не зміниться. і
і  , які вже не є паралельними. Їхні лінії дії перетинаються у певній точці
, які вже не є паралельними. Їхні лінії дії перетинаються у певній точці 
 . (1.23)
. (1.23) . (1.24)
. (1.24) дорівнює сумі двох векторів:
дорівнює сумі двох векторів: , (1.25)
, (1.25) .(1.26)
.(1.26) . (1.27)
. (1.27) і відшукаємо точку
і відшукаємо точку 
 називають центром паралельних сил
називають центром паралельних сил  і
і  .
.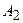 . Легко також зрозуміти, що поняття центра паралельних сил можна поширити на три, чотири і більше паралельних сил.
. Легко також зрозуміти, що поняття центра паралельних сил можна поширити на три, чотири і більше паралельних сил.


