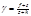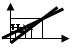Часткова і загальна рівновага. Взаємодія ринків продуктів і ресурсів.

Отже, однією із особливостей ринкової економіки є те що рівновага на окремому ринку залежить від рівноваги на інших ринках. В умовах вільної конкуренції сукупність цін на товари відповідає стану загальної рівноваги (рівноваги на всіх ринках), якщо задовольняють наступні вимоги:

- всі споживачі максимізують свою корисність за даних бюджетних обмежень;

- всі виробники максимізують свій прибуток за даної технології;

- для кожного блага попит дорівнює пропозиції.

На відміну від аналізу часткової рівноваги, аналіз загальної рівноваги здійснюється з передумови,що ціни і кількість благ на всіх ринках визначаються одночасно з урахуванням факторів зворотних зв’язків. Ефектом зворотного зв’язку називають зміну ціни і кількості товару на деякому ринку у відповідь на аналогічні зміни, що виникають на спряжених ринках. Наприклад, зміна ціни на нафту обов’язково позначиться на ринку газу, вугілля, а зміна цін на бензин на ринок автомобілів і т. д.

Велика кількість факторів, що визначають систему рівноважних цін робить моделі загальної економічної рівноваги значно складнішими за ті, що розглядались для часткової рівноваги. Існує дві основні моделі загальної економічної рівноваги: неокласична(або Вальраса) та неокейнсіанська. За допомогою моделей загальної економічної рівноваги пробують відповісти на запитання: за яких умов можливе існування системи цін, яка забезпечує загальну рівновагу на всіх ринках.

Аналіз характеру взаємозв’язку цін благ розглянемо на взаємодії двох ринків за умови що підвищення ціни на одне із благ підвищується попит на інше і навпаки. Для виготовлення благ використовують одні і ті ресурси, а тому в міру підвищення ціни на одне із них зменшується пропозиція іншого. Функції попиту і пропозиції на обох ринках є лінійними:

К^п₁=А+ВЦ₂-СЦ₁; К^П₁=а+вЦ₂-сЦ₁; К^пр₁= -к- l Ц₂+мЦ₁;

К^п₂= д +fЦ₁-nЦ₂; К^пр₂= n-sЦ₁+zЦ₂;

 

Де a,b,c,k, д,l,m, д,f,h,n,s,z – додатні коефіцієнти що відображають характер попиту і пропозиції на ринках.

Вектор рівноважних цін має забезпечити рівновагу одночасно на обох ринках:

К^п₁=К^пр₁; (13.1.)

К^п₂=К^пр₂ (13.2.)

Підставивши відповідні значення функції попиту і пропозиції і вирішивши рівняння (13.1.) і (13.2.) відносноЦ₁ і Ц ₂ отримаємо, що:

Ц₁=α+βЦ₂; (13.3.)

Ц₂=δ+ﻻЦ₂; (13.4.)

Де ,

Рівняння (13.3.) і (13.4.) визначають ціни часткової рівноваги, що забезпечують рівність попиту і пропозиції на одному із ринків за заданої ціни на іншому ринку, рівноваги на якому може і не бути. Із цих рівнянь витікає також, що між цінами існує пряма залежність.

Щоб відшукати систему цін, яка забезпечує одночасну рівновагу на обох ринках необхідно вирішити систему рівнянь (13.3.) і (13.4.). Графічне вирішення цієї системи показано на рис. 13.1.: лінія (1) рівняння (13.3.) і лінія (2) рівняння (13.4.).

 

Прямі (1) і (2) побудовані із передумови що коефіцієнти β і g менші за одиницю, а це означає, що попит і пропозиція на кожному із ринків в більшій мірі залежать від ціни цього,а не іншого блага. За таких умов прямі (1) і (2) перетнуться у першому квадранті, а їх спільна точка покаже вектор рівноважних цін Ц^p₁,Ц^p₂, що забезпечує стійку економічну рівновагу господарства, яке складається із двох ринків.

Припустимо, що на першому ринку установилась рівновага за ціни Ц^p₁ (рис. 13.2.). Із рівнянь (13.3.) і (13.4.), або за відповідними прямими на графіку можна установити, що на другому ринку за такої умови буде дефіцит. Ціна другого блага буде зростати, що зумовить підвищення попиту на перше благо і зниження його пропозиції. Внаслідок цього ціна першого блага також буде зростати. Тому, коли ціна на другому ринку підвищиться до Ц^В₂, на першому – вона буде уже вище Ц^А₁. Якщо ціна на першому ринку на цей час прийме значення Ц^С₁, то знову буде рівновага на першому ринку і дефіцит на другому. Так буде до тих пір, поки не сформується система рівноважних цін Ц^p₁ і Ц^p₂.

Аналогічно буде, якщо ціни окажуться вище рівноважного значення. Наближення до рівноважного значення на рис. 13.2. відмічено стрілками. Отже ми маємо стійку загальну економічну рівновагу подібну до часткової стійкої рівноваги.

Якщо параметри функцій попиту і пропозиції будуть такими, що α>0, і δ>0, але β>1 і γ>1 тоді прямі (1) і (2) не будуть перетинатися у першому квадранті, що говорить про те що не існує системи цін, яка б забезпечила спільну рівновагу на обох ринках.

Якщо β>1 і γ>1 а α<0 і δ<0 то це буде вказувати на те, що загальна економічна рівновага двох ринків існує, але вона є нестійкою (рис. 13.3.).

 

 

Тут як і у випадку стійкої рівноваги ми маємо загальну зміну цін на ринках 1 і 2, але ця зміна буде спрямована у зворотному напрямку (віддалення від рівноваги).

Отже за лінійних функцій попиту і пропозиції на двох ринках взаємозамінних благ може існувати стійка спільна рівновага тільки за умови, коли попит і пропозиція кожного з благ в більшій мірі реагують на зміну ціни цього а не іншого блага, тобто коли коефіцієнт прямої цінової еластичності більше за коефіцієнт перехресної цінової еластичності благ.