Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хвильова функція та її статистичний змістСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Корпускулярно-хвильовий дуалізм матерії встановлює межі застосування класичної фізики. В мікросвіті класичний спосіб опису стану частинок за допомогою координат та імпульсів перестає бути однозначним і повинен бути замінений іншим – статистичним способом, на якому грунтується механіка мікросвіту – квантова механіка. Стан мікрочастинок в квантовій механіці задається хвильовою функцією
де
З точки зору хвильових уявлень квадрат амплітуди хвилі визначає її інтенсивність, зокрема, інтенсивність дифракційних максимумів на рис. 7.5. З точки зору корпускулярних уявлень – це імовірність попасти мікрочастинці в ту чи іншу точку екрану спостереження після проходження щілини. Отже, фізичний зміст має не сама хвильова функція, а вираз
Оскільки імовірність повинна бути однозначною, неперервною і скінченою, то на хвильову функцію накладаються наступні стандартні вимоги: 1) вона повинна бути однозначною, неперервною і скінченою; 2) перші похідні по координатах і часу від хвильової функції також повинні бути неперервними, що забезпечить “гладкість” імовірності; 3) вона повинна бути інтегрованою; зокрема, Знання хвильової функції дозволяє встановити середнє значення довільної фізичної величини f:
Для знаходження хвильової функції конкретного квантовомеханічного об’єкту необхідно розв’язати рівняння Шрьодінгера (1926 р.)
яке є аналогом ІІ закону Ньютона класичної механіки. В цьому рівнянні
оператор Гамільтона або оператор повної енергії частинки, де m – маса частинки,
U – оператор потенціальної енергії, дія якого зводиться до простого множення на хвильову функцію. Якщо потенціальна енергія частинки явно не залежить від часу, тобто
Підставляючи (7.28) у (7.25), після нескладних перетворень отримаємо
де с і Е – константи інтегрування, при цьому Е має зміст енергії частинки. Рівняння (7.30) називається рівнянням Шрьодінгера для стаціонарних станів. Розв’язок цього диференціального рівняння задовольняє стандартні вимоги до хвильової функції, як правило, не при усяких, а дискретних (дозволених) значеннях параметра Е. Ці значення називаються власними значеннями оператора Отже, розв’язок рівняння Шрьодінгера (7.30) зводиться до знаходження власних значень і власних функцій оператора повної енергії частинки 7.3.3. Для вільної (U=0) частинки, що рухається вздовж осі х, стаціонарне рівняння Шрьодінгера має вигляд
Розв’язок цього рівняння шукається у вигляді
що легко перевірити підстановкою в рівняння Шрьодінгера. Повна хвильова функція, з врахуванням (7.28) і (7.29),
співпадає з виразом для плоскої хвилі де Бройля (7.19), якщо покласти, що
Рівняння Шреденгера Рівняння руху мікрочастинок мусить враховувати їхні хвильові властивості, тому воно повинне бути хвильовим, подібно рівнянню, яке описує електромагнітні хвилі. Основне хвильове рівняння квантової механіки запропоноване Е.Шредін-гером у 1926 році, і з нього можна одержати аналітичний вираз для y-функцій у кожному конкретному випадку. Його справедливість підтверджується згодою оде-ржаних з його допомогою результатів із дослідними даними. Воно має вид звич-
ля. Відношення w0/V=k – хвильовому числу, яке зв'язане із довжиною хвилі спів-відношенням: k=2p/l. Підставивши сюди вираз довжини хвилі де Бройля частинки l=h/m×V, одержимо рівняння Шредінгера для стаціонарних (незалежних від ча-
льною U(x,y,z). У це рівняння, як параметр, входить повна енергія частинки Е. Із теорії диференціальних рівнянь випливає, що рівняння Шредінгера має рішення не при будь-яких значеннях енергії Е, а лише при певному наборі значень, які називають власними значеннями. Вони можуть утворювати як неперервний, так і дискретний ряд енергій. y-Функції, які відповідають власним значенням енергії, називають власними хвильовими функціями. Найпростішим прикладом вирішення рівняння Шредінгера є рішення задачі про рух частинки у одновимірній потенціальній ямі розміром l із нескінченно високими стінками. Якщо усередині ями на частинку не діють силові поля, то її потенціальна енергія у ямі (для 0£x£l) U(x)=0, а поза ямою (для х<0 і х>l) прямує до нескінченності U(x)=¥. Оскільки частинка не може проникнути за нескінченно високі стінки ями, то y-функція за межами ями дорівнює нулю. Тому, за умови неперервності хвильової функції, вона дорівнює нулю і на межах ями, тобто y(0)=y(l)=0. Усередині ж ями y-функція відмінна від нуля. Хвильове рівняння
=0 маємо y(l)=А×sin(w0×l)=0. Це співвідношення справедливе при умові: w0×l=±p×n,
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.215.30 (0.011 с.) |

 . Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля (7.19), яку представимо тут у комплексній формі:
. Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля (7.19), яку представимо тут у комплексній формі: , (7.21)
, (7.21) . Помноживши
. Помноживши  на комплексно спряжену функцію
на комплексно спряжену функцію  , отримаємо
, отримаємо . (7.22)
. (7.22)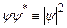 , який називається густиною імовірності. Для частинок, які не є вільними, а перебувають в силових полях, хвильова функція не може розглядатися як просторова хвиля, але її ймовірнісна інтерпретація залишається в силі. Зокрема, імовірність знайти мікрочастинку в деякій області простору, наприклад, в елементарному об’ємі
, який називається густиною імовірності. Для частинок, які не є вільними, а перебувають в силових полях, хвильова функція не може розглядатися як просторова хвиля, але її ймовірнісна інтерпретація залишається в силі. Зокрема, імовірність знайти мікрочастинку в деякій області простору, наприклад, в елементарному об’ємі  , становить
, становить . (7.23)
. (7.23)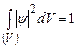 , як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події).
, як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події). . (7.24)
. (7.24) , (7.25)
, (7.25) – (7.26)
– (7.26)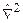 – оператор Лапласа
– оператор Лапласа , (7.27)
, (7.27) , то квантовомеханічна задача називається стаціонарною, і у хвильовій функції можливе розділення змінних, тобто
, то квантовомеханічна задача називається стаціонарною, і у хвильовій функції можливе розділення змінних, тобто . (7.28)
. (7.28)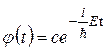 , (7.29)
, (7.29) , (7.30)
, (7.30) , а відповідні хвильові функції
, а відповідні хвильові функції 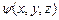 – власними функціями цього оператора.
– власними функціями цього оператора. .
. ,
,
 . Остання рівність є очевидною, оскільки повна енергія частинки співпадає з її кінетичною енергією
. Остання рівність є очевидною, оскільки повна енергія частинки співпадає з її кінетичною енергією . (7.31)
. (7.31)