
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Співвідношення невизначеностей ГейзенбергаСодержание книги
Поиск на нашем сайте
У класичній механіці всяка частинка рухається вздовж певної траєкторії так, що фіксовані її координати та імпульс. Мікрочастинки внаслідок наявності в них хвильових властивостей відрізняються від класичних частинок. Одна з основних відмінностей полягає в тому, що мікрочастинка не має чіткої траєкторії, і неправомірно говорити одночасно про точні значення її координат та імпульсу. Як відомо, будь–яка хвиля, незалежно від її природи, є процесом, що заповнює більшу чи меншу область простору, а через це не може локалізуватися в одній точці. Наприклад, уздовж осі ОХ рухається фотон, для якого точно відомий імпульс Така монохроматична хвиля в просторі нічим не обмежена, область її існування – вся вісь ОХ. Це означає, що в цьому випадку просторовий інтервал Якщо ж область локалізації фотона є обмеженою, то це означає, що амплітуда відповідного хвильового процесу відрізняється від нуля тільки всередині скінченого інтервалу
Чим ширший інтервал Такі висновки справедливі не тільки для фотонів, а й для електронів, протонів та інших мікрочастинок. У 1927 р. В. Гейзенберг, враховуючи хвильові властивості мікрочастинок, дійшов до висновку, що об’єкт мікросвіту неможливо одночасно з однаковим ступенем точності характеризувати і координатами, й імпульсом. Згідно з співвідношенням невизначеностей Гейзенберга мікрочастинка не може одночасно мати і певні координати
тобто добуток невизначеностей координати і відповідної їй проекції імпульсу не може бути меншим від величини Співвідношення невизначеностей випливає з хвильових властивостей мікрочастинок. Нехай потік фотонів проходить через вузьку щілину завширшки
Звідки
З теорії дифракції відомо, що першому дифракційному мінімуму при дифракції світла на нескінченно довгій щілині відповідає куту
Або
З (1.10) і (1.11) маємо
З останнього співвідношення отримуємо
Якщо врахувати дифракційні максимуми вищих порядків, то
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.009 с.) |

 , тобто
, тобто  . Такому фотону відповідає хвиля, довжина якої однозначно визначається величиною імпульсу
. Такому фотону відповідає хвиля, довжина якої однозначно визначається величиною імпульсу  .
.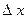 , в якому замкнено об’єкт з хвильовими властивостями – фотон, дорівнює нескінченності. Іншими словами, при
, в якому замкнено об’єкт з хвильовими властивостями – фотон, дорівнює нескінченності. Іншими словами, при 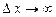 . Отже, якщо точно відомий імпульс, локалізація фотона стає цілком невизначеною.
. Отже, якщо точно відомий імпульс, локалізація фотона стає цілком невизначеною. і дорівнює нулю поза ним. Такий хвильовий процес уже не можна зобразити монохроматичною хвилею. Його можна уявити як суперпозицію ряду монохроматичних хвиль різної довжини. На рис. 4.3 наведено простий приклад суперпозиції трьох синусоїдальних хвиль, внаслідок чого виникає хвильовий процес – так званий хвильовий пакет, амплітуда якого відрізняється від нуля в скінченому інтервалі
і дорівнює нулю поза ним. Такий хвильовий процес уже не можна зобразити монохроматичною хвилею. Його можна уявити як суперпозицію ряду монохроматичних хвиль різної довжини. На рис. 4.3 наведено простий приклад суперпозиції трьох синусоїдальних хвиль, внаслідок чого виникає хвильовий процес – так званий хвильовий пакет, амплітуда якого відрізняється від нуля в скінченому інтервалі 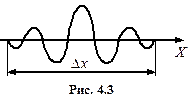 Оскільки в хвильовому пакеті є набір значень
Оскільки в хвильовому пакеті є набір значень  , які містяться в деякому інтервалі
, які містяться в деякому інтервалі  , то набір значень імпульсів Pзнаходиться в інтервалі
, то набір значень імпульсів Pзнаходиться в інтервалі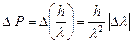 . (1.8)
. (1.8)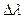 можливих значень інтерферуючих хвиль, а разом з тим інтервал
можливих значень інтерферуючих хвиль, а разом з тим інтервал 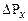 можливих значень імпульсів, тим вужча область локалізації
можливих значень імпульсів, тим вужча область локалізації 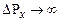 маємо
маємо  ,тобто точне значення координат фотона можливе тільки при повній невизначеності його імпульсу.
,тобто точне значення координат фотона можливе тільки при повній невизначеності його імпульсу. і певні відповідні проекції імпульсу
і певні відповідні проекції імпульсу  , причому невизначеності в значеннях цих всіх величин задовольняють умови
, причому невизначеності в значеннях цих всіх величин задовольняють умови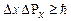 ,
,  ,
,  , (1.9)
, (1.9) .
.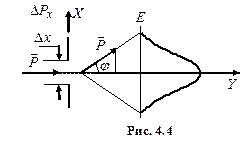 До проходження через щілину фотони рухалися вздовж осі OY, тому складова
До проходження через щілину фотони рухалися вздовж осі OY, тому складова 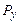 їх імпульсу
їх імпульсу  є точно визначена, відповідно складова
є точно визначена, відповідно складова 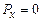 та
та  імпульсу фотонів. В той самий час координата x фотонів є цілком невизначеною. В момент проходження фотонів через щілину їх положення в напрямку осі ОX визначається з точністю до ширини щілини, тобто з точністю
імпульсу фотонів. В той самий час координата x фотонів є цілком невизначеною. В момент проходження фотонів через щілину їх положення в напрямку осі ОX визначається з точністю до ширини щілини, тобто з точністю  . Отже, появиться невизначеність в значенні складової імпульсу вздовж осі ОХ, яка дорівнює
. Отже, появиться невизначеність в значенні складової імпульсу вздовж осі ОХ, яка дорівнює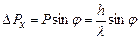 . (1.10)
. (1.10) (1.11)
(1.11)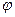 дифракції, що задовольняє умову:
дифракції, що задовольняє умову: .
. . (1.12)
. (1.12)
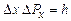 . (1.13)
. (1.13) або
або  . (1.14)
. (1.14)


