Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки с и d лежат на окружности с диаметром АВ. Прямые ac и BD пересекаются в точке Р, а прямые AD и bс – в точке Q. Докажите, что прямые AB и pq перпендикулярны.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Доказать: Доказательство.
Рассмотрим
№15. Прямая проходит через центр квадрата со стороной 1. Найдите сумму квадратов расстояний от всех вершин квадрата до этой прямой.
Найти: Решение.
Ответ:
Вариант 6. №13. В прямоугольном треугольнике АВС проведена высота CD к гипотенузе АВ. Найдите АВ, если
Найти: АВ Решение. Пусть
Ответ:
№14. На стороне АВ параллелограмма ABCD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма. Дано: ABCD – параллелограмм, Найти: Решение.
Тогда
Ответ:
№15. Каждая диагональ четырехугольника делит его на два равновеликих треугольника. Докажите, что данный четырехугольник – параллелограмм.
Доказать: ABCD – параллелограмм Доказательство. Дополнительное построение: Т.к. Аналогично
Вариант 7. №13. Два круга с радиусами по 5 см имеют общую хорду длиной
Найти: Решение. По теореме, обратной теореме Пифагора
Ответ:
№14. Боковые стороны трапеции лежат на перпендикулярных прямых. Докажите, что отрезок соединяющий середины оснований трапеции, равен половине разности длин оснований.
Доказать: Доказательство. Заметим, что, по теореме о четырех замечательных точках трапеции, K, L,M лежат на одной прямой.
№15. В треугольнике АВС проведена биссектриса АК. Центр окружности, вписанной в треугольнике АВК и центр окружности, описанной около треугольника АВС, совпадают. Найдите углы треугольника АВС.
Найти: Решение. Т.к. О – центр вписанной и описанной окружностей Пусть
Тогда получим для
Ответ:
Вариант 8. №13. Две стороны треугольника имеют длины 10 см и 6 см, а медиана, проведенная к третьей стороне, равна 7 см. Найдите угол между данными сторонами треугольника.
Найти: Решение.
По теореме косинусов:
Ответ:
№14. В треугольник АВС вписан квадрат так, что две его вершины лежат на стороне АВ и по одной вершине на сторонах АС и ВС. Найдите площадь квадрата, если АВ=40 см, а высота, проведенная из вершины С, имеет длину 24 см.
Найти: Решение.
Тогда
Ответ:
№15. Вне квадрата на его стороне, построен прямоугольный треугольник, у которого сторона квадрата является гипотенузой. Докажите, что биссектриса прямого угла этого треугольника проходит через центр квадрата.
Дано: ABCD – квадрат, Доказать: NM проходит через центр ABCD Доказательство. Достроим BCDАN до квадрата со стороной BN+AN, Пусть О – центр квадрата NLMK, тогда
Вариант 9. №13. Докажите, что если диагонали трапеции перпендикулярны, то сумма квадратов их длин равна квадрату суммы длин оснований.
Доказать: Доказательство. Дополнительное построение: По теореме Пифагора:
№14. В треугольник вписана окружность радиуса 4 см. Одна из сторон треугольника разделена точкой касания на отрезки 6 см и 8 см. Найдите длины сторон треугольника.
Найти: Решение.
Пусть
Тогда Ответ: №15.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1037; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.251 (0.007 с.) |

 Дано:
Дано:  ,
,  ,
,  , AC
, AC  BD=Р, AD
BD=Р, AD 
 и
и  - прямоугольные, т.к. опираются на диаметр.
- прямоугольные, т.к. опираются на диаметр. :
:  - точка пересечения высот
- точка пересечения высот  Дано: ABCD – квадрат,
Дано: ABCD – квадрат,  ,
,  .
.
 ,
,  -прямоугольные,
-прямоугольные,  ,
,  - общий, тогда
- общий, тогда  , значит,
, значит,  . Аналогично
. Аналогично  , значит,
, значит, 

 .
. Дано:
Дано:  - прямоугольный, CD – высота,
- прямоугольный, CD – высота, 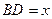 , тогда
, тогда  , т.е.
, т.е. 


 ,
, 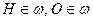 , AC
, AC 


 , т.к. О – середина BD, К – середина АВ
, т.к. О – середина BD, К – середина АВ 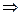 КО – средняя линяя
КО – средняя линяя  , аналогично
, аналогично 
 , как углы, опирающиеся на диаметр
, как углы, опирающиеся на диаметр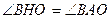 , т.к. они опираются на одну дугу
, т.к. они опираются на одну дугу 
 , т.к.
, т.к. 
 , как накрест лежащие при
, как накрест лежащие при  (из
(из 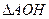 )
)

 Дано: ABCD – четырехугольник, AC
Дано: ABCD – четырехугольник, AC 
 .
. BD – общая, то
BD – общая, то  ,
,  , как вертикальные углы,
, как вертикальные углы, 
 , аналогично
, аналогично  - параллелограмм, ч.т.д.
- параллелограмм, ч.т.д. см. Найдите площадь общей части этих кругов.
см. Найдите площадь общей части этих кругов. Дано: Окр(О;R), Окр(O1;R), B, D – точки пересечения, R=5см,
Дано: Окр(О;R), Окр(O1;R), B, D – точки пересечения, R=5см,  см.
см.
 - прямоугольный (
- прямоугольный ( ),
), 


 см
см Дано: ABCD – трапеция,
Дано: ABCD – трапеция,  ,
,  .
.
 , тогда
, тогда  - прямоугольный,
- прямоугольный, 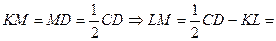
 , ч.т.д.
, ч.т.д. Дано:
Дано:  - описана около
- описана около  - вписана в
- вписана в  ,
,
 , тогда
, тогда 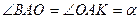



 ,
, 
 Дано:
Дано: 


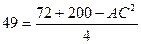




 Дано:
Дано: 


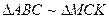 (по двум углам)
(по двум углам)


 см2
см2
 - прямоугольный, NM-биссектриса.
- прямоугольный, NM-биссектриса.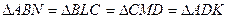 (по трем сторонам).
(по трем сторонам). , значит,
, значит, 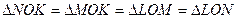 - прямоугольные и равнобедренные
- прямоугольные и равнобедренные  , т.е. NM и LK – биссектрисы
, т.е. NM и LK – биссектрисы  , значит, биссектрисы пересекаются в центре NLMK
, значит, биссектрисы пересекаются в центре NLMK  , т.е. О – центр ABCD, ч.т.д.
, т.е. О – центр ABCD, ч.т.д. Дано: ABCD – трапеция,
Дано: ABCD – трапеция,  .
.
 ,
, 
 , т.е.
, т.е. 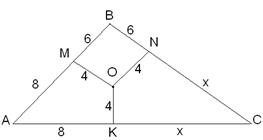 Дано:
Дано:  - вписана в
- вписана в  ,
, 

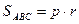 , с другой стороны
, с другой стороны 
 , тогда получим:
, тогда получим: