
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В треугольнике abc угол a больше угла b, а угол b больше угла C. К какой из вершин треугольника ближе всего расположен центр вписанной в него окружности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найти: к какой из вершин треугольника ближе всего расположен центр вписанной в него окружности Решение: Поскольку O – центр вписанной окружности, то OA, OB и OC – биссектрисы углов A, B и C соответственно. Т.к. ÐA > ÐB, то Аналогично
№15. Дан прямой угол. Найдите геометрическое место середин всех отрезков одной и той же длины с концами на сторонах этого угла.
Найти: ГМТ Решение.
Ответ: точки
Вариант 14. № 13. В прямоугольном треугольнике ABC (ÐC – прямой) проведена высота CD, а в треугольнике ACD – биссектриса CE. Докажите, что треугольник BCE равнобедренный.
Доказать: DBCE – равнобедренный. Доказательство. Так как CE – биссектриса ÐACD, то ÐACE = ÐECD. ÐBCE = ÐACB - ÐACE = 90° - -ÐECD, ÐBEC = 180° - ÐADC - ÐECD = 90°- -ÐECD Þ ÐBCE = ÐBEC Þ DBCE – равнобедренный. № 14. В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой одного из углов трапеции. Определите, в каком отношении диагонали трапеции делятся точкой пересечения.
Дано: ABCD – равнобокая трапеция AB = CD, AC ^ CD, AC Ç BD = O, AC –биссектриса ÐA Найти: Решение. Так как трапеция – равнобокая и АС – биссектриса Ответ:
№ 15 Треугольник ABC – равносторонний со стороной, равной a. На расстоянии a от вершины A взята точка D. Найдите угол BDC.
Дано: DABC – равносторонний, AB = = BC = AC = AD = a Найти: Решение. Построим окружность с центром в точке A и радиусом, равным a. Тогда точки B, C и D лежат на этой окружности, а градусная мера меньшей дуги BC равна 60° (поскольку ÐBAC – центральный для этой окружности и равен 60°). Рассмотрим 2 случая: 1) пусть D лежит на большей дуге BC окружности (на чертеже эта точка обозначена как D1). Тогда ÐBDC – вписанный и опирается на меньшую дугу BC и, потому, равен половине её градусной меры, то есть 30°; 2) пусть D лежит на меньшей дуге BC окружности (на чертеже эта точка обозначена как D2). Тогда ÐBDC – вписанный и опирается на большую дугу BC и, потому, равен половине её градусной меры, то есть 150°. Примечание: Если точка D совпадает с одной из точек B или C, что вполне возможно согласно условию задачи, то ÐBDC = 0° Ответ: 30° или 150°
Вариант 15 № 13. В треугольнике ABC биссектриса AE равна отрезку EC. Найдите углы треугольника ABC, если известно, что AC = 2AB.
Найти: ÐA, ÐC, ÐB Решение. Так как AE – биссектриса ÐA, то ÐBAE = ÐCAE. Так как AE = EC, то DAEC – равнобедренный Þ ÐBAE = ÐCAE = ÐC Þ ÐA = 2ÐC. Пусть M – середина AC. Тогда AB = AM = MC, поскольку AC = 2AB, Þ EM – медиана DAEC, а так как DAEC равнобедренный, то EM – высота DAEC Þ ÐAME = 90°. Так как по условию AC=2AB и М – середина АС, то AB = AM=МС, ÐBAE = ÐCAE, AE – общая сторона, то DABE = DAME Þ ÐB = ÐAME = 90°. ÐA + ÐB + ÐC = 180°, а так как ÐB = 90°, ÐA = 2ÐC, то 3ÐC = 90° Þ ÐC = 30° Þ ÐA = 60°. Ответ: ÐA = 60°, ÐC = 30°, ÐB = 90°. № 14. В равнобокую трапецию с острым углом 30° вписана окружность. Найдите отношение длины окружности к периметру трапеции.
Найти: Решение. Пусть BH – высота трапеции. Тогда BH = 2r, где r – радиус окружности. Поскольку трапеция является описанной около окружности, то AB+CD = BC + AD, а так как AB = CD (трапеция равнобокая), то AB = Так как DABH – прямоугольный, а ÐA = 30°, то BH = Ответ: № 15. Внутри треугольника ABC взята точка D такая, что ÐABD = ÐACD = 45°. Докажите, что отрезки AD и BC перпендикулярны и равны, если угол BAC равен 45°.
Доказать: AD = BC, AD Доказательство. Пусть BD Ç AC = B1, CD Ç AB = C1, AD Ç BC = A1. Тогда BB1 ^ AC, поскольку ÐAB1B = 180° - ÐA - ÐABD = 90°, Þ BB1 – высота DABC. Аналогично CC1 – высота DABC Þ D – точка пересечения высот DABC Þ AA1 – высота DABC Þ AD ^ BC. Так как DABB1 – равнобедренный, то AB1 = BB1. Также DB1DC – равнобедренный, поэтому B1D = B1C. Тогда треугольники AB1D и BB1C равны по двум катетам Þ AD = BC, ч.т.д..
Вариант 16. №13. В трапеции ABCD диагонали АС и BD перпендикулярны. На большем основании AD выбрана точка М так, что ВМ=MD=3 см. Найдите длину средней линии трапеции.
Найти: Решение. I способ Т.к. ВМ=MD, то
BN –биссектриса и высота
Ответ:
Дополнительное построение: LBCA – параллелограмм (
Ответ:
Т.к. ВМ=MD, то
BН –биссектриса и высота Пусть ВС=ВО=х, тогда ОМ=3-х
Ответ:
№14.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.17 (0.008 с.) |

 Дано: DABC, ÐA > ÐB >ÐC, O –центр вписанной в DABC окружности
Дано: DABC, ÐA > ÐB >ÐC, O –центр вписанной в DABC окружности ÐA >
ÐA > 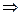
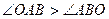 , а т.к. в треугольнике против большего угла лежит большая сторона
, а т.к. в треугольнике против большего угла лежит большая сторона 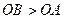 .
.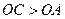 (из
(из 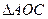 ). Таким образом, центр вписанной в треугольник ABC окружности ближе всего расположен к вершине A.
). Таким образом, центр вписанной в треугольник ABC окружности ближе всего расположен к вершине A. Дано:
Дано:  - прямоугольный,
- прямоугольный,  ,
, 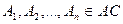 ,
, 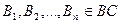 ,
, 
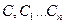
 - прямоугольные, тогда
- прямоугольные, тогда  , значит,
, значит,  точки
точки  лежат на дуге окружности с центром в точке С и
лежат на дуге окружности с центром в точке С и 
 Дано: DABC, ÐC = 90°, CD – высота DABC, CE – биссектриса DACD
Дано: DABC, ÐC = 90°, CD – высота DABC, CE – биссектриса DACD
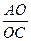
 , то ÐBAC = ÐCAD = ÐBDC = ÐBDA Þ ÐCAD = 90° - 2ÐCAD Þ ÐCAD = 30° Þ
, то ÐBAC = ÐCAD = ÐBDC = ÐBDA Þ ÐCAD = 90° - 2ÐCAD Þ ÐCAD = 30° Þ 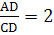 , а так как OD – биссектриса DACD, то
, а так как OD – биссектриса DACD, то 



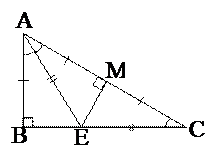 Дано: DABC, AE – биссектриса ÐBAC, AE = EC, AC = 2AB
Дано: DABC, AE – биссектриса ÐBAC, AE = EC, AC = 2AB Дано: ABCD – равнобокая трапеция с основаниями AD и BC, ÐA = ÐD = = 30°, Окр.(О;r) - вписанная
Дано: ABCD – равнобокая трапеция с основаниями AD и BC, ÐA = ÐD = = 30°, Окр.(О;r) - вписанная
 .
. .
. 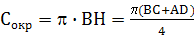 ,
,  Þ Þ
Þ Þ  .
.
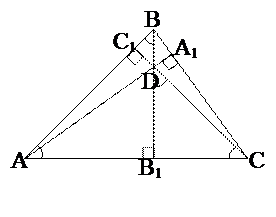 Дано: DABC, ÐA = 45°, D
Дано: DABC, ÐA = 45°, D 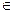 DABC, ÐABD = ÐACD = 45°
DABC, ÐABD = ÐACD = 45° BC
BC Дано: ABCD – трапеция,
Дано: ABCD – трапеция,  , ВМ=MD=3 см.
, ВМ=MD=3 см.
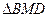 - равнобедренный
- равнобедренный 
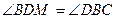 как накрест лежащие при
как накрест лежащие при  и секущей BD.
и секущей BD. - равнобедренный и ВК=ВС
- равнобедренный и ВК=ВС  , KN=NC
, KN=NC как накрест лежащие при
как накрест лежащие при 
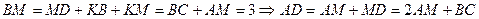 , т.е.
, т.е. 
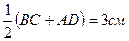
 II способ
II способ
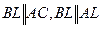 )
) 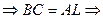

 .
.  - равнобедренный
- равнобедренный  ,
,  - равнобедренный
- равнобедренный  длина ВМ численно равна длине средней линии трапеции и ВМ=3см
длина ВМ численно равна длине средней линии трапеции и ВМ=3см III способ
III способ - равнобедренный и ВК=ВС
- равнобедренный и ВК=ВС  (
( как накрест лежащие при
как накрест лежащие при  - равнобедренный АМ=ОМ=3-х
- равнобедренный АМ=ОМ=3-х




