
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найдите углы треугольника, Если высота и медиана, проведенные из одной вершины, делят угол при этой вершине треугольника на три равные части. ⇐ ПредыдущаяСтр 6 из 6
Найти: ÐA, ÐC, ÐB Решение.
Тогда Ответ:
№ 15. Две окружности пересекаются в точках A и B, прямая CD – общая касательная этих окружностей (C и D – точки касания). Прямые AB и CD пересекаются в точке N. Докажите, что N – середина CD.
Дано: w1 и w2 – окружности, w1 Ç Ç w2 = {A;B}, CD – общая касательная, CD Ç w1 = C, CD Ç w2 =D, AB Ç CD = N Доказать: CN = ND Доказательство. По теореме о квадрате касательной для окружности w1 имеем:
Вариант 17. №13. В прямоугольной трапеции ABCD высота АВ равна сумме оснований AD и ВС. Биссектриса угла АВС пересекает сторону CD в точке К. В каком отношении эта точка делит CD?
Найти: Решение. I способ Пусть EF – средняя линия ABCD. Проведем BF и AF,
Ответ:
Пусть
ВК – биссектриса равнобедренного треугольника с основанием МС Ответ:
Пусть BK Ç AD = L. Так как BK – биссектриса ÐB, а ÐB = 90°, то ÐABL = = ÐCBL = 45°. Так как AL װ BC, то ÐBCD = ÐCDL, ÐABL = ÐCBL = ÐL = = 45° Þ DABL – равнобедренный Þ AB = AL. Так как AB = AD + BC, AL = = AD + DL, а AB = AL, то AD + BC = AD + DL Þ BC = DL. Так как ÐBCD = = ÐCDL, ÐCBL = ÐL, BC = DL, то DBCK = DDKL Þ CK = KD Þ Ответ:
№14. В окружность диаметра
Найти: Решение. I способ
Ответ:
Пусть Сумма всех углов шестиугольника
Итак Ответ:
№15. На окружности с центром О дана точка А. найдите геометрическое место середин всех хорд этой окружности, проведенных из точки А.
Найти: ГМТ точки М Решение. Пусть точка B1 окружности такая, что точка O не лежит на отрезке AB1. Пусть O1 – середина AO. Тогда, поскольку M1 – середина AB1 и O1 – середина AO, O1M1 – средняя линия в DAOB1 Þ O1M1 = ½OB1 = ½R. Таким образом, точка M1 удалена от данной точки O1 на данное расстояние, равное ½R. Тогда, в силу произвольности выбора точки B1, все точки M лежат на данном расстоянии от точки O1, то есть, на окружности с центром в точке O1 и радиусом, равным ½R. Докажем, что все точки этой окружности принадлежат искомому ГМТ. Выберем произвольно точку M2 этой окружности. Пусть прямая AM2 пересекает данную окружность в точке B2. Докажем, что M2 – середина AB2. Так как AO = OB2, то DAOB2 – равнобедренный Þ ÐOAB2 = ÐOB2A. Также AO1 = O1M2, поэтому DAO1M2 – равнобедренный Þ ÐOAB2 = ÐO1M2A Þ ÐOB2A = ÐO1M2A Þ O1M2 װ OB2, а так как O1 – середина AO, то по теореме Фалеса M2 – середина AB2. Итак, искомое ГМТ – окружность с центром в середине отрезка AO и радиусом, равным половине этого отрезка.
Ответ: Вариант 18. № 13. Найдите радиус окружности, описанной около равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
Найти: R Решение. SD = R = Ответ: № 14. Точки M и N – середины сторон CD и BC параллелограмма ABCD. Докажите, что отрезки AM и AN делят диагональ BD на три равные части.
Дано: ABCD – параллелограмм, MС=MD, NB=NC, AMÇBD = K, ANÇBD = L Доказать: DK = KL = LB Доказательство. Так как ABCD – параллелограмм, то AB = DC, AD = BC, AB║CD, AD║BC. Так как M – середина CD, то DM = ½CD = ½AB Þ № 15. На гипотенузе AB прямоугольного треугольника ABC выбрана произвольная точка M, и из неё опущены перпендикуляры MK и MP на катеты этого треугольника. Определите, при каком положении точки M длина отрезка PK будет наименьшей.
Дано: DABC, ÐC = 90°, M Найти: при каком положении точки M длина отрезка PK будет наименьшей. Решение. Заметим, что CKMP – прямоугольник Þ PK = CM при любом положении точки M на гипотенузе. Значит PK минимально только в том случае, если CM минимально, а минимальное расстояние от точки C до прямой AB есть отрезок перпендикуляра, опущенного из точки C на прямую AB. Значит M – основание высоты, опущенной из вершины C на гипотенузу.
Ответ: M – основание высоты, опущенной из вершины C на гипотенузу.
Вариант 19. № 13.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.174.248 (0.024 с.) |
 Дано:
Дано:  , медиана СМ, СН - высота,
, медиана СМ, СН - высота, 
 : СН – биссектриса, тогда, по свойству биссектрисы угла треугольника,
: СН – биссектриса, тогда, по свойству биссектрисы угла треугольника, 



 ,
, 

 . Аналогично, для окружности w2 получаем:
. Аналогично, для окружности w2 получаем:  . Значит CN2 = ND2 Þ CN = ND Þ N – середина CD, ч.т.д.
. Значит CN2 = ND2 Þ CN = ND Þ N – середина CD, ч.т.д. Дано: ABCD – прямоугольная трапеция,
Дано: ABCD – прямоугольная трапеция,  ,
,  - биссектриса,
- биссектриса,  .
.
 , также
, также  - равнобедренный,
- равнобедренный,  ;
; - биссектриса,
- биссектриса,  - средняя линия и
- средняя линия и 

 II способ
II способ , тогда
, тогда  - равнобедренный
- равнобедренный 
 также равнобедренный
также равнобедренный 
 - прямоугольный
- прямоугольный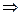 ВК – серединный перпендикуляр к
ВК – серединный перпендикуляр к  центр описанной вокруг
центр описанной вокруг  окружности лежит на ВК, но он также лежит на CD, как на гипотенузе. В
окружности лежит на ВК, но он также лежит на CD, как на гипотенузе. В  II способ
II способ .
. см вписан шестиугольник, одна сторона которого 10 см, а все остальные равны между собой. Найдите его углы.
см вписан шестиугольник, одна сторона которого 10 см, а все остальные равны между собой. Найдите его углы. Дано:
Дано:  ,
,  ,
,  .
.

 по теореме косинусов
по теореме косинусов









 II способ
II способ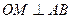 . В
. В 
 - равнобедренный
- равнобедренный 



 Дано:
Дано:  ,
, 

 Дано: DABC, AB = AC = 13, BC = 10.
Дано: DABC, AB = AC = 13, BC = 10.
 .
.

 Аналогично
Аналогично  . Так как AB║CD, то DABK ~ DDKM Þ
. Так как AB║CD, то DABK ~ DDKM Þ  Þ
Þ  Þ Þ DK =
Þ Þ DK =  BD –
BD –  DK =
DK =  BD. Аналогично из подобия треугольников ALD и BLN получаем: BL =
BD. Аналогично из подобия треугольников ALD и BLN получаем: BL = 
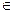 AB, MK ^ AC, MP ^ BC
AB, MK ^ AC, MP ^ BC


