Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окружность, касающаяся гипотенузы прямоугольного треугольника и продолжений его катетов, имеет радиус R. Найдите периметр треугольника.
Найти: Решение. KOMC – квадрат, т.к.
KA=AN, NB=BM как отрезки касательных, проведенных из одной точки, тогда Ответ:
Вариант 2. №13. Три окружности с радиусами 1 см, 2 см и 3 см попарно касаются друг друга. Найдите длину окружности, проходящей через центры данных окружностей.
Найти: Решение. Известно, что точка касания двух окружностей лежит на прямой, соединяющей их центры, тогда В
прямоугольный
Ответ:
№14. Найдите площадь трапеции, основания которой 16 см и 28 см, а диагонали 17 см и 39 см.
Найти: Решение. Дополнительное построение: Пусть Рассмотрим прямоугольный
Рассмотрим прямоугольный по теореме Пифагора
Ответ:
№15. Даны две точки А и В на плоскости. Укажите геометрическое место точек М этой плоскости, для которых А, В и М – вершины равнобедренного треугольника. Дано:
М Решение. 1) Если в искомом треугольнике
2) Если в искомом треугольнике
3) Если в искомом треугольнике
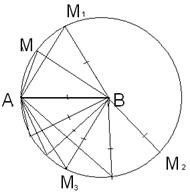
Вариант 3. №13. Через вершину В равнобедренного треугольника АВС параллельно основанию АС проведена прямая BD. Через точку К – середину высоты ВН проведен луч АК, пересекающий прямую BD в точке D, а сторону ВС в точке N. Определите, в каком отношении точка N делит сторону ВС.
Найти: Решение.
Пусть
Ответ: №14. Найдите площадь трапеции, основания которой 6 см и 26 см, а боковые стороны 12 см и 16 см.
Найти: Решение. Дополнительное построение: достроим трапецию до параллелограмма
По формуле Герона
Ответ: II способ
Дополнительное построение
Ответ:
№15. Дана трапеция, в которую можно вписать окружность. Докажите, что окружности, построенные на ее боковых сторонах как на диаметрах, касаются друг друга.
Доказать: Окр(О1;r) и Окр(О2;R) касаются Доказательство. Пусть N, K, M, L – точки касания вписанной в трапецию окружности со сторонами трапеции, тогда
Итак, Q – тоска касания, ч.т.д.
Вариант 4. №13. Две касающиеся окружности с центрами О1 и О2 лежат внутри окружности с центром О и радиусом R касаются ее в двух различных точках. Найдите периметр треугольника ОО1О2.
Найти: Решение. Известно, что точка касания двух окружностей лежит на прямой, соединяющей их центры, тогда Пусть А, В, С – точки касания окружностей, тогда
Но Ответ:
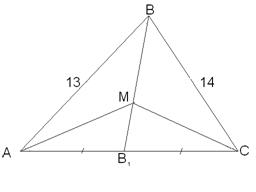
№14. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку пересечения медиан М с вершинами треугольника. Найдите площадь треугольника ВМС.
Найти: Решение.
По формуле Герона
Ответ:
№15. Каждая высота параллелограмма не меньше той стороны, которой она перпендикулярна. Докажите, что параллелограмм является квадратом.
Доказать: ABCD - квадрат Доказательство. Рассмотрим 2 случая: 1)
С другой стороны 2) Итак,
Вариант 5. №13. В равнобокой трапеции, площадь которой равна
Дано: ABCD – трапеция, Найти: Решение. Дополнительное построение:
Дополнительное построение:
Ответ:
№14.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.200.143 (0.036 с.) |
 Дано:
Дано:  - прямоугольный, окр.(О;R) касается гипотенузы и продолжений катетов в точках K, N, M,
- прямоугольный, окр.(О;R) касается гипотенузы и продолжений катетов в точках K, N, M, 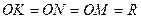

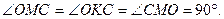
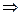
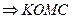 -прямоугольник, но OK=OM=R.
-прямоугольник, но OK=OM=R.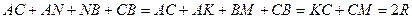

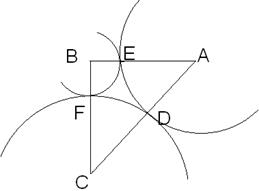 Дано: Окр(A;2), Окр(B;1), Окр(C;3), E, F, D – точки касания, Окр
Дано: Окр(A;2), Окр(B;1), Окр(C;3), E, F, D – точки касания, Окр  (О;ОА),
(О;ОА),

 ,
, 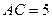 ,
,  .
.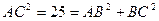 , тогда по теореме, обратной теореме Пифагора,
, тогда по теореме, обратной теореме Пифагора,  . Тогда
. Тогда 
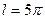
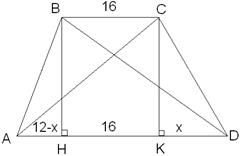 Дано: ABCD – трапеция,
Дано: ABCD – трапеция, 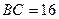 см,
см,  см,
см, 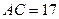 см,
см, 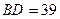 см
см
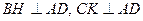 .
. , тогда
, тогда 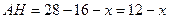 .
.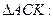
 - по теореме Пифагора
- по теореме Пифагора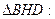
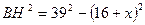
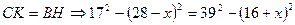


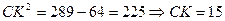
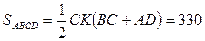 см2
см2 см2
см2
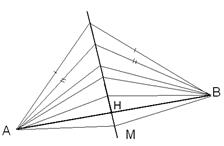 Найти: ГМТ точки М, где А, В и М – вершины равнобедренного треугольника.
Найти: ГМТ точки М, где А, В и М – вершины равнобедренного треугольника.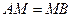 , то
, то  , где
, где 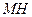 - серединный перпендикуляр, т.к. все точки, равноудаленные от концов отрезка, лежат на серединных перпендикулярах.
- серединный перпендикуляр, т.к. все точки, равноудаленные от концов отрезка, лежат на серединных перпендикулярах.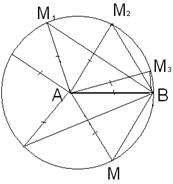
 , то
, то 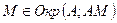
 , то
, то 
 Дано:
Дано: 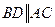 ,
, 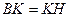 ,
,  ,
, 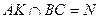 .
.
 (
( ,
,  )
) ,
, 
 (
( ,
,  )
)

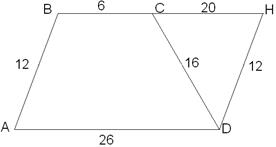 Дано: ABCD – трапеция,
Дано: ABCD – трапеция, 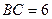 см,
см, 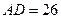 см,
см,  см,
см,  см.
см. .
.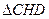 :
: 
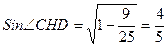
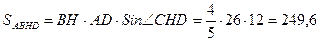
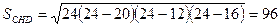
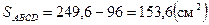
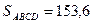 см2
см2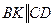 , тогда
, тогда  . По формуле Герона
. По формуле Герона  , с другой стороны
, с другой стороны  .
.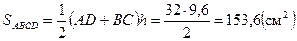
 Дано: ABCD – трапеция, Окр. (О; R`) – вписанная, Окр(О1;r), Окр(О2;R),
Дано: ABCD – трапеция, Окр. (О; R`) – вписанная, Окр(О1;r), Окр(О2;R), 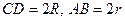
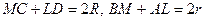 (по свойству отрезков касательных)
(по свойству отрезков касательных) 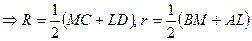
 - средняя линяя трапеции
- средняя линяя трапеции 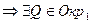 и
и 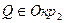 . Очевидно, что общая точка единственна.
. Очевидно, что общая точка единственна. Дано: Окр. (О; R), Окр(О1;r), Окр(О2;R`) –касаются друг друга.
Дано: Окр. (О; R), Окр(О1;r), Окр(О2;R`) –касаются друг друга.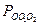
 и
и 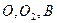 , и
, и 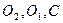 - лежат на одних и тех же прямых.
- лежат на одних и тех же прямых. (т.к.
(т.к. 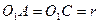 )
) (т.к.
(т.к.  )
)
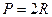
 Дано:
Дано: 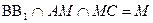 - медианы,
- медианы, 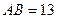 см,
см, 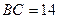 см,
см, 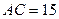 см
см
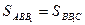 ,
, 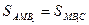 , т.к.
, т.к. 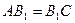 , высота общая
, высота общая  , аналогично
, аналогично 
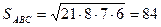

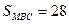 см2
см2 Дано: ABCD – параллелограмм,
Дано: ABCD – параллелограмм,  ,
,  ,
,  ,
, 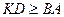 .
. ,
, 
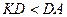 (т.к. AD – гипотенуза прямоугольного треугольника AKD)
(т.к. AD – гипотенуза прямоугольного треугольника AKD) 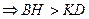
 - получено противоречие, значит, утверждение не верно и
- получено противоречие, значит, утверждение не верно и  ,
, 
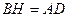 ,
, 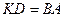 , т.е.
, т.е.  ,
,  - квадрат, ч.т.д.
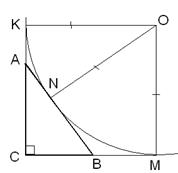
- квадрат, ч.т.д.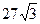 см2, одно из оснований в два раза больше другого. Диагональ трапеции является биссектрисой острого угла. Найдите основания трапеции.
см2, одно из оснований в два раза больше другого. Диагональ трапеции является биссектрисой острого угла. Найдите основания трапеции.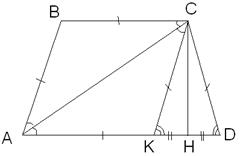
 ,
,  , АС – биссектриса
, АС – биссектриса  .
.
 .
.
 - равносторонний и
- равносторонний и 
 , т.к.
, т.к.  равносторонний, то СН – высота, медиана и биссектриса.
равносторонний, то СН – высота, медиана и биссектриса.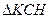 - прямоугольный,
- прямоугольный,