
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель оценки текущей стоимости облигаций, реализуемых с дисконтом без выплаты процентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Модель доходности дисконтных облигаций: по эффективной ставке процента: YTM = по ставке простых процентов: YTM = где Рk - курс облигации (отношение цены покупки к номинальной стоимости облигации); Т - количество календарных дней в году; t - количество дней до погашения облигации. Предположим, требуется определить уровень доходности облигаций к погашению, если цена покупки - 850 руб., цена выкупа (номинал) - 1(300 руб., срок обращения облигации - 90 дней: по эффективной ставке процента: YТМ = по ставке простых процентов: YТМ = Для оценки текущей стоимости акции при ее использовании в течение неопределенного периода времени используют обычно следующую модель: PVакц = где РVαкц - текущая стоимость акции, используемой в течение неопределенного периода времени; Dt - предполагаемая к получению сумма дивидендов в t- мпериоде; d - альтернативная норма доходности в виде десятичной дроби; t - число периодов, включенных в расчет. Текущая стоимость акций со стабильным уровнем дивидендов определяется отношением суммы годового дивиденда к рыночной норме доходности: РVакц = Di ∕ d = 200 ∕ 0,15 = 1333 руб. Для определения текущей стоимости акций, используемых в течение определенного срока, используется следующая модель: РVакц = где КС - курсовая стоимость акции в конце периода ее реализации; п - число периодов использования акции. Пример. Номинальная стоимость акции - 1000 руб., уровень дивидендов - 20%, ожидаемая курсовая стоимость акции в конце периода ее реализации - 1100 руб., рыночная норма доходности 15%, период использования акции - 3 года, периодичность выплаты дивидендов - раз в году. РVакц = Доход от акций состоит из суммы полученных дивидендов и дохода от прироста их стоимости. Текущая доходность определяется отношением суммы дивидендов по акции за последний год к курсовой стоимости акции: Yтек = Курсовая стоимость акции рассчитывается в сравнении с банковской депозитной ставкой (rd): Ра = Конечная доходность акции (Y) - это отношение суммы совокупного дохода к первоначальной ее стоимости: Y = где D 1 - доход в виде полученных дивидендов; Р 1- рыночная цена акции на текущий момент, по которой она может быть реализована; Р 0- цена покупки акции; Yd - дивидендная доходность акции; Yс - капитализированная доходность акции. Предположим, что предприятие приобрело два года назад пакет акций по цене 10 тыс. руб. за каждую. Текущая рыночная цена акции составляет 15 тыс. руб., а сумма полученных дивидендов на одну акцию за этот период - 3 тыс. руб. Отсюда суммарный доход от одной акции равен 8 тыс. руб. [3 + (15 – 10)], а общая ее доходность составляет 80% (8 ∕ 10 × 100), в том числе дивидендная доходность - 30% (3 ∕ 10 × 100), капитализированная доходность - 50% [(15 – 10) ∕ 10 × 100]. Пользуясь приведенными моделями, можно сравнивать выгодность инвестиций в различные финансовые инструменты и выбирать наиболее оптимальный вариант инвестиционных проектов. При этом следует учитывать, что доходность вложений, выраженная в разных валютах, несопоставима. К примеру, если процентная ставка в рублях выше, чем процентная ставка в валюте, то нельзя сделать вывод о выгодности вложения денег в рублевый депозит. Допустим, что акция была куплена за 10 000 руб., а через год продана за 12 000 руб. Ее годовая доходность составит Yr = Если акция была куплена при курсе доллара 25 руб., а продана при курсе 28,57 руб., то цена покупки в долларах - 400 дол., а цена продаж - 420 дол. Доходность в валюте равна Ys = Если бы курс доллара повысился еще в большей степени, то доходность этой финансовой операции была бы вообще отрицательной. Доходность в рублях и доходность в инвалюте связаны следующим соотношением: Yr = Ys = где Yr - доходность в рублях; Ys - доходность в валюте; К 2, К 1- курс валюты при продаже и при покупке соответственно. Следовательно, зная курсы валют и доходность финансового актива в одной из валют, можно определить его доходность в другой валюте. Уровень доходности инвестиций в конкретные ценные бумаги зависит от следующих факторов: - изменения уровня процентных ставок на денежном рынке ссудных капиталов и курса валют; - ликвидности ценных бумаг, определяемой временем, которое необходимо для конвертации финансовых инвестиций в наличные деньги; - уровня налогообложения прибыли и прироста капитала для разных видов ценных бумаг; - размера трансакционных издержек, связанных с процедурой купли-продажи ценных бумаг; - частоты и времени поступления процентных доходов; - уровня инфляции, спроса и предложения, других факторов.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.199 (0.009 с.) |

 =711,7
=711,7  ;
;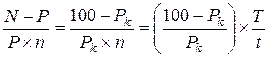 ,
, – 1 = 91,5%;
– 1 = 91,5%; = 70,6%.
= 70,6%. ,
, ,
, = 1178 руб.
= 1178 руб. × 100%.
× 100%. × 100%.
× 100%.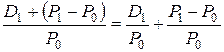 = Yd + Yc.
= Yd + Yc.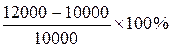 = 20%.
= 20%. = 5%.
= 5%. × (1 + 0,05) – 1 = 0,2 (20%),
× (1 + 0,05) – 1 = 0,2 (20%), × 1,2 – 1 = 0,05 (5%),
× 1,2 – 1 = 0,05 (5%),


