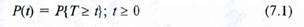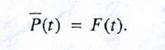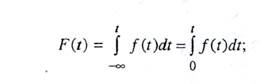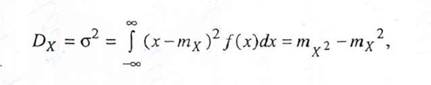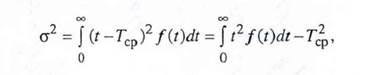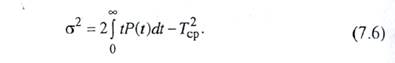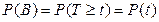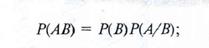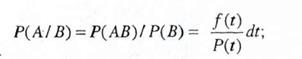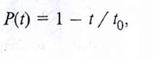Надежность систем. Оценка вероятности отказов и вероятности безотказной работы системы при различных схемах соединения входящих в нее элементов.

Надежность — один из показателей качества, однако часто этот показатель является основным, определяющим качество и эффективность продукции, в первую очередь технических объектов. Иногда обеспечение надежности есть главное условие безопасности работы объекта.

В соответствии с ГОСТ 27.002-89 под надежностью понимают свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Показатели надежности характеризуют свойства объекта сохранять во времени в установленных пределах значения всех параметров и требуемых функций. Надежность объекта включает четыре показателя: безотказность, долговечность, ремонтопригодность и сохраняемость. В зависимости от назначения продукции и условий ее применения могут использоваться как все, так и некоторые из указанных показателей.

Под объектом понимается техническое изделие определенного назначения, например машины, сооружения, аппараты, приборы, их узлы и отдельные детали. Иногда в теории надежности объект рассматривается как система, состоящая из совокупности отдельных элементов, взаимодействующих между собой.

В соответствии со стандартом надежность — это свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров в пределах, установленных нормативно-технической документацией, называется работоспособностью. Состояние, при котором хотя бы один из указанных параметров не соответствует требованиям, — неработоспособность. Событие, состоящее в нарушении работоспособности, называется отказом. Процесс обнаружения и устранения отказа с целью перевода объекта из неработоспособного состояния в работоспособное называется восстановлением.

Иногда восстановление неработоспособного объекта невозможно или нецелесообразно. Предельное состояние объекта – это такое состояние, при котором дальнейшее применение объекта по назначению должно быть прекращено из-за неустранимого нарушения требований безопасности, неустранимого отклонения заданных параметров за установленные пределы, недопустимого увеличения эксплуатационных расходов или необходимости проведения капитального ремонта.

Продолжительность работы объекта называется наработкой. При работе объекта с перерывами учитывается суммарная наработки, Различают наработку до первого отказа, наработку между отказа ми и др. Наработка может измеряться как в единицах времени, так и в других единицах, например, циклах, километрах пробега и т.п. Наработка объекта от начала его эксплуатации до достижения предельного состояния называется техническим ресурсом. Срок службы объекта – это календарная продолжительность его эксплуатации от ее начала до наступления предельного состояния.

Надежность – комплексное свойство объекта, включающее его безотказность, ремонтопригодность, долговечность и сохраняемость.

Безотказность – свойство объекта непрерывно сохранять, работоспособность в течение некоторого времени или наработки. Основными показателями безотказности являются вероятность безотказной работы, интенсивность отказов, средняя наработка до первого отказа и другие. Безотказность чрезвычайно важна для некоторых механизмов автомобилей (тормозная система, рулевое управление).

Ремонтопригодность – приспособленность объекта к предупреждению и обнаружению отказов, к восстановлению работоспособного состояния путем технического обслуживания и ремонта. Основные показатели ремонтопригодности – вероятность восстановления, интенсивность восстановления, среднее время восстановления, средняя наработка на отказ (отношение наработки восстанавливаемого объекта к математическому ожида­нию числа отказов в течение этой наработки), коэффициент готовности (отношение времени, в течение которого объект находится в работоспособном состоянии, к общей длительности периода) и другие.

Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Основные показатели долговечности – средний ресурс, гамма-процентный ресурс (наработка, в течение которой объект не достигает предельного состояния с заданной вероятностью 1 – γ), средний ресурс до капитального ремонта, средний срок службы и другие.

Сохраняемость – свойство объекта сохранять работоспособное состояние после хранения и (или) транспортировки. Сохраняемость играет важную роль для пищевой продукции. Основные показатели сохраняемости – средний срок сохраняемости и гамма-процентный срок сохраняемости.

 

Предполагается, что отказ – событие случайное, поэтому время работы объекта до первого отказа Т – случайная величина.

Вероятностью безотказной работы (или функцией надежности) называется вероятность события, состоящего в том, что время до первого отказа окажется не ниже некоторой заданной величины t, называемой наработкой до отказа.

 

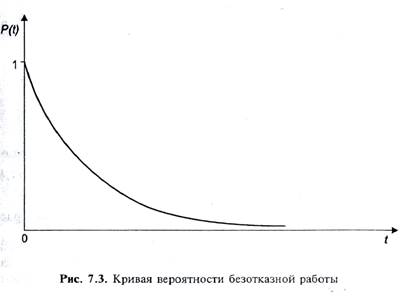
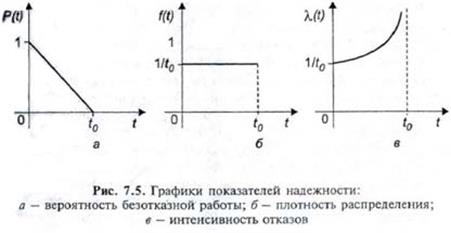
Естественно предположить, что в момент включения объект считается работоспособным: при t = 0 P(0)= 1. С увеличением наработки t эта функция убывает до нуля (рис. 7.3).

Нетрудно видеть, что вероятность отказа есть функция распределения случайной величины Т:

Если функция F(t) дифференцируема, то для характеристики безотказности может использоваться плотность распределения (рис. 7.4)

Учитывая, что

Соответственно

получим

(использовано условие нормировки — площадь под кривой распределения равна единице).

Из формулы (7.4) следует, что вероятность безотказной работы соответствует площади под кривой распределения от за данного момента t до бесконечности (на рис.7.4, б заштрихована). Элемент вероятности f(t) dt - это вероятность того, что случайная величина Т примет значение, лежащее в пределах малого участка (t, + ∆t).

Средняя наработка до отказа есть математическое ожидание времени безотказной работы. Учитывая, что математическое ожидание непрерывной случайной величины определяется по формуле

 

тогда

 

Нетрудно видеть, что первое слагаемое в этом выражении равно нулю, тогда

таким образом, средняя наработка на отказ численно равна площади под кривой вероятности безотказной работы P(t).

Используя формулы для дисперсии непрерывной случайной величины

можно по аналогии с (7.5) получить зависимость для дисперсии времени безотказной работы:

откуда

Предположим, что событие А = {отказ объекта при Т < t +dt}, а событие В = {отказ объекта при Т ≥ t}. Вероятность

— это вероятность безотказной работы объекта. Тогда произведение этих событий АВ = {отказ в промежутке t ≤Т < t + dt}, вероятность этого события(использовано свойство функции распределения и определение плотности распределения). По формуле умножения вероятностей

здесь Р(А/В) — вероятность отказа объекта в промежутке (t,t+ dt) при условии, что он не отказал до момента t

 

эта вероятность пропорциональна отрезку времени dt, а коэффициент пропорциональности называется интенсивностью отказов. Отметим, что при t = 0 P(t)=1, поэтому λ(0) =f(0).

Уравнение прямой вероятности безотказной работы

 

Рассмотрим надежность объекта, полагая, что он состоит из n элементов (узлов). Допустим, надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом.

Параллельно-последовательная структура надежности сложного изделия дает представление о связи между надежностью изделия и надежностью его элементов. Расчет надежности ведется последовательно - начиная от расчета элементарных узлов структуры к ее все более сложным узлам. Расчет надежности сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов.