Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гистограмма- это инструмент, позволяющий зрительно оценить закон распределения статистических данных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. По оси ординат откладывают абсолютные значения частот. Гистограмма очень удобна и для визуальной оценки расположения статистических данных в пределах допуска. Чтобы оценить адекватность процесса требованиям потребителя, необходимо сравнить качество процесса с полем допуска, установленным пользователем. В данном случае на гистограмму необходимо нанести верхнее (SLU) и нижнее (SL) значения поля допуска в виде линий, перпендикулярных оси абсцисс, чтобы сравнить распределение параметра качества процесса с требованиями потребителей, что позволяет увидеть, как располагается гистограмма внутри этих линий. Существуют два способа построения гистограммы. Первый способ. На заранее заготовленный контрольный листок наносят метки (крестики) соответствующих размеров и производят их подсчет. Совместное расположение меток (крестиков) на контрольном листке характеризует форму гистограммы. Второй способ. Предусматривает выполнение следующих этапов: 1. Разработка контрольного листка. На данном этапе нужно обратить внимание на два момента. Во-первых, нужно помнить, что гистограмма будет достоверно отражать картину изменений процесса при наличии не менее 50 случайных результатов измерений, причем оптимальным является 100 измерений, когда вероятность ошибки составляет не более 0,02. Во-вторых, в контрольном листке необходимо учесть столбцы, строки и ячейки, позволяющие максимально упростить последующие расчеты. 2. Заполнение контрольного листка. 3. Вычисление выборочного размаха. В контрольном листке с данными находятся наибольшие и наименьшие выборочные значения и вычисляется размах R:
4. Определение размеров классов. Размеры классов определяются так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов R делят на число, чтобы получилось от 5 до 20 интервалов равной ширины (h) Можно подсчитать количество классов другим способом: число интервалов должно примерно соответствовать корню квадратному из общего количества данных. При числе данных 30-50 количество интервалов должно быть 5-7; при числе данных 50-100 – 6-10; при числе данных 100-250 – 7-12. Нужно помнить, что для удобства дальнейших расчетов лучше всего использовать нечетное число классов. 5. Определение границ класса. На данном этапе нужно помнить, что числовые диапазоны первого и последнего классов соответственно должны включать наименьшее и наибольшее значения, полученные опытным путем и внесенные в контрольный листок. Вначале находят наименьшее (нижнее) граничное значение для первого класса:
где Xmin - наименьшее выборочное значение, Единица измерения – порядок точности замеров. Далее к полученному значению прибавляют ширину h интервала, чтобы получить максимальное (верхнее) значение границы первого класса. При определении минимального и максимального значений второго класса нужно: минимальному значению границы второго класса присвоить максимальное значение границы первого класса, и прибавить ширину h к нижней границе второго класса для получения верхней и т.д. 6. Вычисление середины класса. Середина класса вычисляется по следующей формуле:
где Н - нижняя граница класса, В - верхняя граница первого класса. Середины второго, третьего и последующих классов можно получить прибавлением ширины классов (Л). 7. Подготовка вспомогательной таблицы. Для облегчения дальнейших расчетов и построения гистограммы удобно использовать вспомогательную таблицу, указанную на рис. 2.1. 8. Подсчет частот. Определить, в какой класс входит каждое значение контрольного листка, указав их в виде палочек в столбце "частота". Далее нужно подсчитать количество попаданий (частоту) в каждом классе и определить суммарную частоту ∑f. Если ∑f больше или меньше количества данных, указанного в контрольном листке, необходимо данный пункт повторить заново, т.е. опять определить, к какому классу принадлежит каждое значение. 9. Вычисление среднего арифметического и стандартного отклонения. 10. Построение диаграммы. На горизонтальной оси откладывают значения параметров (интервалы), а на вертикальной оси - частоту попадания данных в соответствующий интервал. Для каждого класса строят прямоугольник (столбик) с основанием, равным ширине интервала класса, и высотой, соответствующей частоте попадания данных в этот интервал. На график наносятся средняя арифметическая линия и линии, представляющие границы допуска, если они есть. На чистом поле указываются следующие данные: период, в течение которого собирались данные, число данных п, среднее арифметическое X, стандартное отклонение S. По рисунку гистограммы можно определить состояние проверяемого параметра (процесса). Различают следующие модификации формы гистограммы: а) симметричная гистограмма (нормальное распределение). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам, вырисовывая колоколообразную форму (рис. 2.2). Эта форма встречается чаще всего и говорит о стабильности контролируемого параметра или процесса. б) гребенка. Классы через один имеют более низкие частоты (рис. 2.3). Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.
в) положительно скошенное распределение (рис. 2.4а) или отрицательно скошенное распределение (рис. 2.46). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно – вправо (влево). Форма асимметрична; встречается, когда нижняя (верхняя) граница регулируется либо теоретически, либо по значению допуска, или когда левое (правое) значение недостижимо. г) двугорбая гистограмма. Такая гистограмма содержит два возвышения, которые чаще всего имеют разную высоту, с провалом между ними (рис. 2.5). Гистограмма указывает на случаи объединения двух распределений с разными средними значениями (например, в случае наличия разницы между двумя станками, между двумя рабочими и т.д.). В данном случае необходимо провести расслоение и исследовать причины выявленных различий.
Рис. 2.4. Скошенное распределение: а - положительное, б - отрицательное
д) плато (равномерное и прямоугольное распределения). Частоты в разных классах образуют плато, поскольку все классы имеют более или менее одинаковые ожидаемые частоты с конечными классами (рис. 2.6). Такая форма встречается в смеси нескольких распределений, имеющих различные средние арифметические. е) гистограмма в форме обрыва слева (справа), у которой обрезан один край (рис. 2.7). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты спадают при движении влево (вправо) резко и, наоборот, вправо (влево) – медленно. Указанная форма встречается при стопроцентном рассеивании изделий из-за плохой воспроизводимости процесса.
ж) гистограмма с отдельным островком. Подобная форма появляется при наличии малых включений данных из другого распределения, например, в случае нарушения нормальности процесса, появления ошибки измерения или включения данных из другого процесса (рис. 2.8). з) гистограмма с прогалом (с "вырванным зубом"). Такая гистограмма (рис. 2.9) получается, когда ширина интервала класса не кратна единице измерения (не выражается целым числом выбранной единицы измерения), когда оператор ошибается в считывании показателей шкалы, и т.д. Если гистограмма имеет симметричный (колоколообразный) вид, то можно предположить о гауссовском (нормальном) законе распределения случайной величины. В этом случае среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается в обе стороны. Эта форма встречается чаще всего на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. Термин "нормальный" в данном случае не совсем удачен. Многие признаки подчиняются нормальному закону, например, дальность полета снаряда, рост человека и т.п. Но если какой-либо признак подчиняется другому, отличному от нормального, закону распределения, то это не означает, что процесс, связанный с этим признаком, протекает "ненормально".
Гистограмма имеет дело с измеряемыми данными (температура, толщина) и их распределением. Распределение может быть критическим, т.е. иметь максимум. Многие повторяющиеся события дают результаты, которые изменяются во времени. Гистограмма обнаруживает количество вариаций, которые имеет процесс. Типичная гистограмма может выглядеть так, как показано на рис.
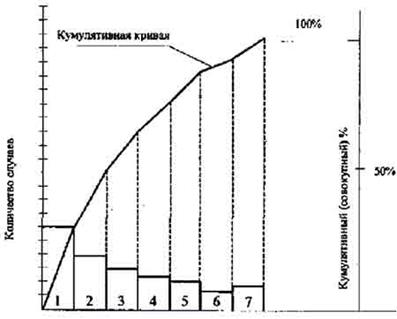
ДИАГРАММА ПАРЕТО Столбиковая диаграмма, названная именем итальянского экономиста В.Парето (1845-1923), который изобрел формулу, показывающую неравномерность распределения благ, а именно, наибольшая доля доходов или благ принадлежит небольшому числу людей, но они дают наибольшую отдачу. Подобное распределение для классификации проблем качества на немногочисленные существенно важные и многочисленные несущественные впервые применил американский ученый Дж. Джуран и назвал этот метод анализом Парето, согласно которому в большинстве случаев подавляющее число дефектов и связанных с ними потерь возникает из-за относительно небольшого числа причин. Суть диаграммы Парето заключается в том, что при ее построении выявляется статистическая закономерность, так называемый "закон 80/20", означающий, что если число дефектов принять за 100%, то примерно 80% всех дефектов происходит из-за приблизительно 20% всех возможных причин. Таким образом, экономически целесообразным будет устранить 1/5 часть причин, приносящих наибольший ущерб. Диаграмма Парето строится в несколько этапов. Этап 1. Определение проблемы и метода сбора данных: 1) выбор типа проблемы исследования; 2) выбор необходимых данных и их классификация (нечасто встречающиеся признаки классифицируются под заголовком "прочие"); 3) определение метода и периода сбора данных. Этап 2. Разработка контрольного листка для регистрации данных с перечнем видов собираемой информации. Этап 3. Заполнение контрольного листка и подсчет итогов. Этап 4. Расположение полученных данных в порядке убывания значимости (группа "прочие" помещается в конец последовательности вне зависимости от числового значения). Этап 5. Графическое изображение диаграммы Парето. Начертить одну горизонтальную и две вертикальные оси. На левой вертикальной оси наносится шкала с интервалом от 0 до числа, соответствующего общему итогу. Правая вертикальная ось - шкала с интервалом от 0 до 100% (причем число 100% должно стоять на одной горизонтальной линии с числом на левой оси, соответствующим общему итогу). На горизонтальной оси указывается количество контролируемых признаков (с учетом группы "прочие"). Этап 6. Построение столбиковой диаграммы в порядке убывания значимости контролируемых признаков (на основе результатов этапа 4). Этан 7. Расчет и черчение кумулятивной кривой. Этап 8. Нанесение на диаграмму всех обозначений (название, разметка числовых значений на осях, наименование контролируемого изделия, имя составителя диаграммы) и надписей (период сбора информации, объект исследования и место его проведения, общее число объектов контроля). Выделяют следующие виды диаграмм Парето. 1. Диаграмма Парето по результатам деятельности. Предназначена для выявления главной проблемы, отражающей негативные результаты деятельности (дефекты, поломки, ошибки, отказы, рекламации, ремонт, возвраты продукции, объем потерь, затраты, нехватка запасов, ошибки в составлении счетов, срыв сроков поставок, несчастные случаи, трагические ошибки, аварии и т.д.). 2. Диаграмма Парето по причинам. Отражает причины проблем, возникающих в ходе производства, с целью выявления главной из них (например, для причины рабочий -это смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики и т.д.). При построении диаграмм Парето нужно придерживаться следующих правил: 1. Для эффективного анализа нужно пользоваться разными классификациями и составлять несколько диаграмм Парето, т.к. суть проблемы можно уловить, наблюдая явление с разных точек зрения. 2. Нежелательно, чтобы группа "прочие" факторы составляла большой процент, т.к. скорее всего объекты наблюдения расклассифицированы неправильно и слишком много объектов попало в одну группу. 3. Если данные можно представить в денежном выражении, лучше всего показать это на вертикальных осях диаграммы Парето. При использовании диаграммы Парето для контроля важнейших факторов наиболее распространенным методом анализа является так называемый ABC-анализ, сущность которого заключается в том, что все причины разбиваются на три группы. К первой группе, группе А, относится небольшое число причин, которые оказывают существенное воздействие на исследуемую проблему. Данная категория позволяет выявить причины, где скрываются 60–70% потенциальных решений для улучшения, и, затратив минимум усилий, можно получить максимум эффекта. Вторая группа, группа С, состоит из большого числа причин, оказывающих незначительное воздействие на объект исследования. Данная категория позволяет решить проблему всего на 5–10%, затратив при этом максимум усилий. Поэтому причины, входящие в группу С (чаще всего это группа "прочие"), сразу откидывают в связи с экономической неэффективностью их анализа и дальнейшего улучшения. Оставшаяся третья группа, группа В, содержит в себе 25-30% потенциальных решений для улучшения, к которым прибегают в двух случаях. Во-первых, иногда невозможно или неэффективно анализировать причины, входящие в группу А (нет опыта на предприятии по решению данной проблемы, повышенные затраты и т.д.). Во-вторых, когда исчерпаны все варианты решений первой группы, а значительного результата не достигнуто. Для удобства ABC-анализа необходимо на диаграмме Парето начертить кумулятивную кривую, указывающую суммарную весомость причин. Данная кривая строится следующим образом: во-первых, необходимо подсчитать общую сумму значений причин, которую нужно принять за 100%. Далее, во-вторых, необходимо подсчитать весомость каждой причины в процентах. В-третьих, первой точке кумулятивной кривой присвоить значение наиболее весомой причины (первой по порядку на диаграмме Парето). В-четвертых, вторая точка определяется как сумма весомостей первой и второй причин и т.д. В-пятых, необходимо соединить точки между собой линией. При прибавлении весомости категории "прочие" результат суммирования должен равняться 100%. Поэтому, используя кумулятивную кривую, легко определить, какие категории причин входят в группы А, В и С. Таким образом, выяснив источники появления "немногочисленных существенно важных" дефектов (группа А), можно устранить почти все потери, сосредоточив внимание на ликвидации именно этих причин, отбросив из рассмотрения те источники, которые приводят к отдельным "многочисленным несущественным" дефектам, на исправление которых затрачиваются значительные усилия. Диаграмму Парето целесообразно применять вместе с причинно-следственной диаграммой. Чтобы решить выявленную серьезную проблему, необходимо уяснить сущность явления каждой конкретной причины. В подобной ситуации собирают по возможности большее число заинтересованных лиц и начинают всесторонне изучать коренную причину недоброкачественности. В результате построения причинно-следственной диаграммы останавливаются на четырех-пяти причинах, требующих первоочередного внимания. После проведения корректирующих мероприятий диаграмму Парето можно вновь построить для изменившихся в результате коррекции условий и проверить эффективность проведенных улучшений. Построение диаграммы Парето, основанное или на контрольных листках или на других формах сбора данных помогает привлечь внимание и усилия к действительно важным проблемам. Можно достичь большего, занимаясь самым высоким столбиком, не уделяя внимание меньшим столбикам.
Рис. Диаграмма Парето
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1854; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)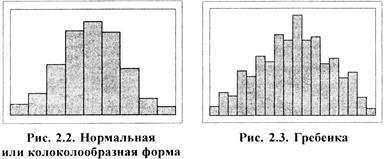

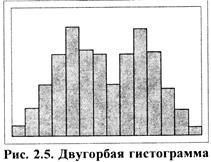
 Рис. 2.6. Плато
Рис. 2.6. Плато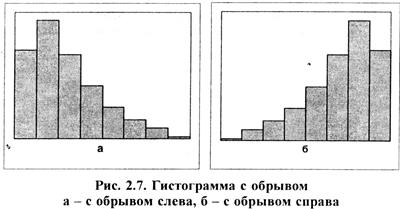
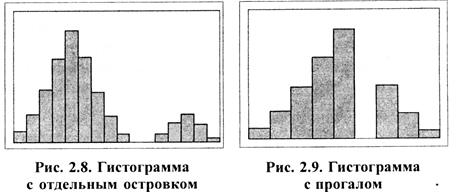
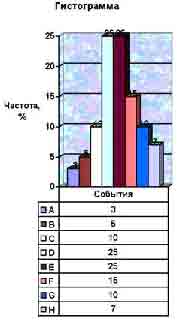 Рис. Гистограмма
Рис. Гистограмма