Оценивание возможностей процесса

Обычно подлежит изучению следующая переменная величина (параметр процесса) или характеристика:

· известная важная или важнейшая

· предположительная ненадежная

· по которой нужно получить информацию о возможностях процесса

· эксплуатационная, имеющая значение при маркетинге

При этом не следует контролировать все величины одновременно. Контрольные карты стоят денег, поэтому нужно использовать их разумно:

· тщательно выбирать характеристики

· прекращать работу с картами при достижении цели

· продолжать вести карты только тогда, когда процессы и технические требования сдерживают друг друга

Необходимо иметь в виду, что процесс может быть в состоянии статистического регулирования и давать 100% брака. И наоборот, может быть неуправляемым и давать продукцию, на 100% отвечающую техническим требованиям. Контрольные карты позволяют проводить анализ возможностей процесса. Возможности процесса – это способность функционировать должным образом. Как правило, под возможностями процесса понимают способность удовлетворять техническим требованиям.

 

16. Выборочный контроль по альтернативным признакам и оперативная характеристика. Понятие риска поставщика и риска и производителя, а также оптимальности планов контроля.

При приемке партии продукции контроль может быть сплошным, когда контролируется каждая единица продукции (например, под­шипник, бутылка воды, моток провода и т.п.). Такой контроль чаще всего экономически необоснован, а иногда и невозможен. Более распространен выборочный контроль, когда заключение о качестве партии продукции делается на основе анализа выборки ограниченного объема. Выборочный контроль подразделяется:

• по времени проведения: на входной (закупочный контроль сырья и полуфабрикатов), промежуточный (межоперационный) и выходной (приемка и сертификация готовой продукции);

• по изменениям в результате контроля: на разрушающий и неразрушающий (например, для контроля прочности изделия его необходимо довести до разрушения);

• по жесткости: на нормальный, усиленный (более сложный) и облегченный; переход с одного вида контроля на другой производится в зависимости от количества партий, которые были пос­ледовательно приняты, или наоборот, отклонены потребителем;

• по контролируемому параметру: на количественный (в этом случае производится измерение контролируемого показателя качества продукции) и качественный (в частности, наиболее распространен контроль по альтернативному признаку, когда о каждом контролируемом объекте делается заключение, годен он или негоден, соответствует предъявляемым требованиям или не со­ответствует).

План контроля –это система правил по отбору изделий для проверки (формированию выборок) и принятию решения относительно всей партии – партию принять или забраковать. Забракованная партия или возвращается поставщику, или производится ее сплошной контроль. Применение плана статистического контроля по существу является проверкой статистической гипотезы H₀:. качество партии соответствует предъявляемым требованиям при альтернативной гипотезе H₁: качество партии не соответствует предъявляемым требованиям.

Наиболее распространен контроль по альтернативному признаку. Предположим, что в партии из N изделий имеется М дефектных изделий (М неизвестно). Требуется оценить генеральную долю дефектных изделий q = M/N.

по результатам контроля выборки объемом n изделий, из которых m дефектных.

Различают следующие типы планов контроля:

• одноступенчатый: если среди п изделий число дефектных т не превышает приемочное число с (т < с), то партия принимается, в противном случае партия бракуется;

• двухступенчатый: на первой ступени, если среди n₁ изделий в выборке число дефектных т₁ не превышает приемочное число с₁ (m < с₁), то партия принимается; если т₁ > d₁, где d₁ — браковочное число, то партия бракуется; если же с₁ < m₁< d₁, то принимается решение о взятии второй выборки; на второй сту­пени объемом п₂ с приемочным числом с₂, если суммарное число дефектных изделий не превышает с₂ (m₁ + т₂) < с₂, то партия принимается, в противном случае партия бракуется;

• многоступенчатые планы — обобщение двухступенчатого плана. Берется выборка объемом п₁ и определяется число дефектных изделий т₁; при m₁ < с₁, партия принимается, при с₁ < m₁ < d₁ (d₁> с₁ + 1) принимается решение о взятии второй выборки объемом п₂. Пусть среди (п₁ + п₂) изделий имеется (m₁ + т₂) дефектных, тогда если (m₁ + т₂) < с₂ (с₂ - приемочное число второй ступени), то партия принимается, при с₂ < (m₁+ т₂) < d₂ (d₂> с₂+1), принимается решение о взятии третьей выборки, и т.д. На заключительном k-том шаге, если среди суммы (п₁ + п₂ + +... + n_k) проконтролированных изделий оказалось (т_{ + т₂ + +... + т_к) дефектных и (т₁ + т₂ +... + т_к) с_к, то партия принимается, в противном случае партия бракуется. В многоступенчатых планах число шагов к задается заранее. Обычно п₁ = п₂ =... = п_к.;

• последовательный контроль, при котором решение принимается после оценки ряда выборок, общее число которых заранее не устанавливается, а определяется в процессе контроля по результатам предыдущих выборок. Принимается одно из трех решений – принять партию, забраковать партию, продолжить контроль.

Оперативная характеристика плана

Решение о качестве всей партии изделий принимается по данным выборочных наблюдений. При этом существует два вида рисков:

• в выборке оказалось большое число дефектных изделий, а во всей партии их доля допустима (партия хорошая, а выборка плохая). В этом случае годная партия будет ошибочно забракована – это ошибка первого рода. Вероятность такой ошибки α – риск поставщика. Вероятность приемки партии в этом случае равна (1 – α);

• при сильной засоренности партии дефектными изделиями в выборке может оказаться небольшое количество дефектов (партия плохая, а выборка хорошая) и партия будет ошибочно принята – ошибка второго рода. Вероятность такой ошибки β – риск потребителя.

Требуется дать заключение о качестве партии продукции на основе доли дефектов q (групповой показатель качества продукции). Предположим, что задано нормативное значение этого показателя q₀, обозначаемое в стандартах NQL: NQL = q₀ (Normative Quality Level). Нормативный уровень несоответствий NQL – это граничное значение уровня несоответствий: партия продукции считается годной к поставке и к использованию потребителем по назначению, если фактический уровень несоответствий не превышает нормативного значения NQL.

Тогда задача состоит в проверке гипотезы о том, что доля дефектных изделий q в партии равна допустимой величине q₀, т.е. Н₀: q = q₀ и при этом сделать риски поставщика и потребителя маловероятными.

Основной вероятностный показатель плана статистического контроля — оперативная характеристика. Это функция P(q), определяющая вероятность приемки партии продукции в зависимости от доли дефектных изделий q = М / N. Очевидно, для каждого плана будет своя оперативная характеристика.

Пусть установлено, что если q < q₀, то качество партии счи­тается хорошим и партию следует принять. При q > q₀ партию следует забраковать. В идеальном случае оперативной характеристикой будет функция P(q) = 1 при 0 < q < q₀, P{q) = 0 при q₀< q < 1 (рис. 5.2). Такая характеристика соответствует плану сплошного контроля при условии, что во время контроля дефект не может быть пропущен.

При выборочном контроле оперативная характеристика – гладкая кривая (см. рис.), при этом Р(0) = 1, т.е. партия, у которой все изделия годные, не может быть забракована; Р(1) = 0: партия, у которой все изделия дефектные, не может быть принята.

 

P(q)

 

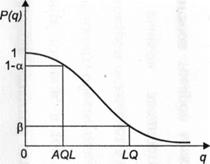
Рис.

0 q

Обычно партии разделяют на «хорошие» и «плохие» с помощью двух чисел: q₀ = AQL (Acceptable Quality Level) – приемлемый уровень качества, q₁= LQ (Limiting Quality) – предельное качество.

Приемлемый уровень качества AQL – максимальный уровень несоответствий в партии продукции, который считается удовлетворительным при приемке (по устаревшей, но используемой на практике терминологии – приемочный уровень дефектности). При контроле на основе этого показателя большинство предъявленных партий будет принято, если их уровень несоответствий не превышает заданного значения AQL.

Предельное качество LQ (в устаревшей терминологии – браковочный уровень дефектности) – это минимальный уровень несоответствий, который рассматривается как неудовлетворительный при приемке. При контроле на основе показателя LQ обеспечивается низкая вероятность приемки отдельной партии.

Партии считаются хорошими при q < AQL и плохими при q > LQ. При AQL < q < LQ качество партии считается еще допустимым.

К плану предъявляются требования: вероятность приемки для хорошей партии должна быть не ниже, чем 1 – α, для плохой – не выше риска потребителя β (см. рис.):

P(q) >1– α при q < AQL;

Р(q) < β при q > LQ,

т.е. план сводится к тому, чтобы риски поставщика и потребителя не превышали аиβ.

Пример

При α = 0,05, β =0,1, AQL = 0,003, LQ = 0,02 - для этого плана в среднем из каждых 100 партий, имеющих засоренность не выше 0,3% будет забраковано не более пяти, а из 100 партий, содержащих более 2% дефектных изделий будет принято не более 10 партий.

Контроль по альтернативному признаку – это такой контроль, при котором о каждом контролируемом объекте делается заключение годен он или не годен, соответствует предъявляемым требованиям или не соответствует.

Предположим, что контролируется партия из N изделий. Для контроля делается случайная выборка объемом п. Количество способов, которыми можно выбрать п изделий из N без учета порядка следования - это число сочетаний

Пусть случайная величина X– количество дефектных (несоответствующих) изделий в выборке. Известно, что во всей партии изделий доля несоответствий составляет q. Тогда число дефектных изделий в партии равно Nq, число годных изделий составит N – Nq. Рассмотрим событие X = т – взято ровно т дефектных изделий. Это возможно, если из Nq дефектных изделий взято т изделий, а из оставшихся годных N – Nq взято п – т изделий (всего в выборке п изделий). Тогда вероятность рассматриваемого события

 

(5.1)

Формула (5.1) описывает гипергеометрическое распределение.

Как правило, объем выборки составляет не более 10% от объема всей партии, в этом случае гипергеометрическое распре­деление может быть аппроксимировано биномиальным

 

P(X = m) =C^m_nq ^m(1-q)^n-m. (5.1)

На практике доля несоответствий обычно составляет менее 10%, в этом случае в свою очередь биномиальное распределение может быть аппроксимировано распределением Пуассона:

(5.3)

Рассмотрим одноступенчатый контроль по альтернативному признаку [30, 44]. Вероятность приемки партии P(q) в этом случае — это вероятность того, что количество дефектных изделий т в выборке не превысит приемочное число с. Используя формулу сложения вероятностей несовместных событий, получим уравнение оперативной характеристики одноступенчатого плана контроля:

P(q) = Р(т < с) – Р(Х = 0) + Р(Х = 1)+...+Р(Х = с) =

Подставляя в полученное выражение вместо Р(q) формулу соответствующего распределения (биномиального или гипергеометрического или распределения Пуассона) получают уравнение оперативной характеристики одноступенчатого плана. Подставляя известные значения AQL и LQ, а также заданные риски α и β получают систему нелинейных уравнений, решая которую находят параметры плана - объем выборки п и приемочное число с.

Анализ соответствующих зависимостей показывает, что при постоянном объеме выборки п с возрастанием приемочного числа с вероятность принятия партии с заданным приемлемым уровнем качества AQL возрастает (рис. 5.4, а), а с возрастанием п при постоянном с вероятность приемки партии уменьшается (рис. 5.4, б). Можно подобрать такой план контроля (п,с), который бы обеспечивал значения рисков аир при заданных значениях уровней качества AQL и LQ.

 

 

Рис. 5.4. Оперативные характеристики при п = const (а) и с = const (б)

 

По результатам контроля множества партий продукции могут быть найдены некоторые полезные характеристики, в частности, средняя доля несоответствующих единиц продукции в принятых партиях (средний уровень выходного качества) и среднее число проконтролированных изделий в партии.

Рассмотрим одноступенчатый план, при котором забракованные партии изделий подвергаются сплошному контролю, т.е. контролируются все оставшиеся (N- п) изделия партии, а выявленные дефектные изделия заменяют годными. Предположим, что доля дефектных изделий постоянна и равна q. Тогда с вероятностью P(q) партии изделий принимаются (доля дефектных изделий в ней приблизительно равна q), а с вероятностью [1 - P(q)] партии подвергаются сплошному контролю; доля дефектных изделий в этих партиях равна нулю. Тогда средняя доля дефектных изделий в принятых партиях по формуле математического ожидания для дискретной случайной величины равна:

q_cp=qP(q) + 0[1- P(q)] = qP(q). (5.7)

Величина q_cp и называется средним уровнем выходного качества. Из формулы (5.7) видно, что при q = 0 значение q_c = 0 и при q = 1 также q_cp — 0, поскольку вероятность Р(1) = 0. Так как q_cp — неотрицательная функция от q, равная нулю при q = 0 и q = 1, то внутри интервала 0 < q < 1 средний выходной уровень дефектности имеет максимум q_max (рис. 5.5). Максимальный для заданного плана контроля средний уровень q_max называют пределом среднего уровня выходного качества.

При использовании рассмотренного выше плана, когда забракованные партии изделий подвергаются сплошному контролю, число проконтролированных в партии объема N изделий есть случайная величина, принимающая значение п с вероятностью Р(q) и значение N (сплошной контроль) с вероятностью [1 — P(q)]. Поэтому среднее число проконтролированных изделий в партии равно:

n_cp = nP(q) + N(1 -P(q)). (5.8)

Если же принято решение о возврате забракованной партии поставщику, то объем контроля в этом случае постоянен и равен объему выборки п.

Для уменьшения объема контроля используют многоступенчатые и в частности двухступенчатые планы. Двухступенчатый контроль уменьшает риск поставщика.

При последовательном контроле проверяются изделия, отбираемые из партии случайным образом, и на каждом шаге принимается одно из трех решений: принять партию, отклонить партию или продолжить контроль - взять на контроль следующее изделие. Контроль продолжается до тех пор, пока не накопится информация, достаточная для принятия решения.

При последовательном контроле по альтернативному признаку в качестве исходных данных принимаются риски поставщика α и потребителя Р, приемлемый уровень качества AQL = q₀ и предельное качество LQ= q_v. После задания этих параметров проверяются гипотезы Н₀: q< q₀ или H₁: q> q₁ Используются методы последовательного анализа, которые уже применялись при выводе основных соотношений для контрольных карт кумулятивных сумм. Определяется вероятность P(q₀,n) того, что «проконтролированных изделий принадлежат партии с долей несоответствий, не превышающей q₀; или вероятность P(q_l,n) того, что они принадлежат партии с долей несоответствий не ниже, чем q_v. Для принятия решения находят отношение правдоподобия P(q₁,n) / P(q₀,n).