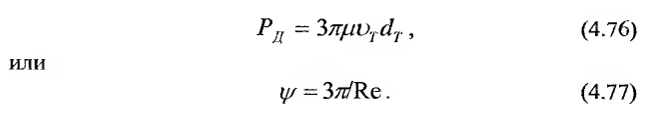Закономерности классификации по трению и упругости

Обогащение (классификация) материала по трению и форме материала основано на использовании различий в скоростях движения разделяемых частиц по наклонной плоскости.

Равнодействующая сил, под действием которых происходит движение частицы (тела) по наклонной плоскости, определяется выражением:

где т - масса частицы; g - ускорение силы тяжести; а - угол наклона плоскости; 1 - коэффициент трения материала о наклонную поверхность, f = tgφ; φ - угол трения.

Скорость движения частицы по наклонной плоскости

где l - длина пути частицы.

Путь, пройденный частицей по горизонтали до разгрузочного устройства

где Н - расстояние по вертикали от конца плоскости до дна разгрузочного устройства.

 

На основании экспериментальных исследований установлено, что коэффициент трения щебня из известняка о металлическую поверхность обратно пропорционален его прочности на сжатие (рис. 6.14).

Рис. 6.14. Зависимости коэффициента восстановления К_в и трения f щебня из известняка от его прочности на сжатие (по данным Н.К. Тимченко)

 

Для обогащения неоднородного по прочности щебня из известняка разработан способ, основанный на использовании различия свойств одновременно как по упругости, так и по трению. Щебень разделяется в процессе удара о поверхность вращающегося барабана (рис. 6.15).

Рис. 6.15. Схема обогащения неоднородного щебня из известняка по упругости и трению на механическом классификаторе Н.К. Тимченко

 

После соударения материал получает две скорости движения: v _t - скорость упругого отскока и ν_к - касательную скорость, вызванную силами трения. Высота падения материала, частота вращения барабана и угол падения подбираются таким образом, чтобы зерна прочного щебня отскакивали под большим углом и падали в противоположную вращению барабана сторону, а зерна слабой прочности - под меньшим углом и падали в сторону вращения барабана. Зерна, которые отскакивают под углом, равным нулю, относят к граничному классу, по которому производится классификация щебня по упругости и трению. Машины для разделения щебня по упругости и трению получили назва­ние механических классификаторов.

Для определения угла падения (разделения) Н.К. Тимченко предложена формула:

где σ_сж - прочность на сжатие, по которой производится классификация (разделение) щебня.

Экспериментальные исследования показали, что крупность щебня (5-50 мм) не влияет существенно на процесс обогащения по упругости и трению. Производительность механических классификаторов увеличивается при обогащении щебня крупных фракций и снижается при классификации щебня мелких фракций.

 

14. ГИДРАВЛИЧЕСКАЯ КЛАССИФИКАЦИЯ НЕРУДНЫХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ

Классификация строительных материалов в жидкой среде, а также гравитационное обогащение (промывка, отсадка, обогащение в тяжелых средах и др.) основаны на различии скоростей падения частиц материала разного размера, формы и плотности в жидких средах.

Падение частиц в жидких средах может быть свободным и стесненным.

Свободное - падение одиночной частицы (тела) в безграничной водной среде или падение тела в жидкости, находящейся в емкости, размеры которой велики по сравнению с размерами падающей частицы (тела).

Стесненное - падение тела в емкости с жидкостью, размеры которой соизмеримы с размерами падающего тела, или падение тела в жидкости, в которой находятся другие частицы, аналогичные падающему телу или отличающиеся от него размерами, формой и плотностью.

В классифицирующем и обогатительном гравитационном оборудовании происходит совместное падение частиц материала. Свободное падение является лишь частным случаем стесненного.

Скорость падения частиц относительно жидкой среды определяется соотношением действующих на частицу сил:

Сила тяжести, направленная вниз, определяется объемом (V) и плотностью частицы (ρ_Т):

g — ускорение силы тяжести (свободного падения).

Подъемная (архимедова) сила, направленная вверх, равна

ρ_ж — плотность жидкой среды.

Гидродинамическое сопротивление возникает вследствие трения жидкости о поверхность тела, а также перепада давления между передней и задней его частью.

Сила гидродинамического сопротивления жидкой среды при движении в ней частицы со скоростью и_т выражается формулой

 

ψ - коэффициент гидродинамического сопротивления;

ρ_ж - плотность жидкой среды;

ν_т - скорость частицы (тела);

d_T - диаметр частицы (тела).

Силы механического взаимодействия частиц определяются массой частиц и скоростью их соприкосновения.

При падении в неподвижной жидкой среде с начальной скоростью (V_т = 0) частица (тело) под действием силы тяжести будет постепенно увеличивать скорость падения. Одновременно будет расти и сила гидродинамического сопротивления (Р_Д). По истечении некоторого времени частица приобретет практически постоянную скорость, называемую конечной скоростью падения. С этого момента сила тяжести (G) и подъемная (архимедова) сила (Р_п) уравновешиваются силой гидродинамического сопротивления (Р_Д). Поэтому для частиц шарообразной формы, когда V=πd_Т ³ /6, можно записать равенство

Коэффициент гидродинамического сопротивления (ψ) зависит от формы и ориентации частицы в пространстве и является функцией безразмерного числа Рейнольдса (Re)

где µ и ν=µ/ρ_ж - соответственно динамический и кинематический коэффициенты вязкости.

Зная зависимость коэффициента сопротивления (ψ) от числа Рейнольдса (Re) по формуле (4.5) можно определить скорость (ν_т) падения частицы (тела) в жидкости. Согласно графику (диаграммы Релея) зависимости коэффициента сопротивления (ψ) от числа Рейнольдса (Re) рассматриваются четыре характерные области:

область малых чисел Рейнольдса (Re<1), где две трети гидродинамического сопротивления составляет сила трения жидкости о поверхность частицы, а одна треть - на долю сопротивления от периода давления (ламинарная область).

Вторая переходная область (1 < Re < 10³), где сила гидродинамического сопротивления характеризуется трением жидкости о поверхность тела и перепадом давления.

Третья область изменения чисел Рейнольдса (10³ < Re < 10⁵),где коэффициент сопротивления является почти постоянной величиной (ψ ≈ 0,16), а сила сопротивления определяется периодом давления (турбулентная область).

Четвертая область резкого снижения коэффициента сопротивления (10⁵ < Re < 3·10⁵), где с увеличением скорости ν _тсила сопротивления уменьшается за счет перехода ламинарной пограничной области в турбулентную.

Скорость падения шаров по теоретическому уравнению может быть рассчитана только для малых чисел Рейнольдса (Re < 1 ), т. е. для ламинарного движения. В этом случае сила гидродинамического сопротивления выражается зависимостью

На основании формул (4.76) и (4.77) скорость падения частицы может быть определена по формуле

 

где Δ = ( ρ_т -ρ_ж )/ ρ_ж- относительная разность плотностей; К = g/18 - постоянный коэффициент.

 

При стесненном падении встречные потоки жидкости, обтекающие потоки материала, движутся в промежутках между ними. Сужение потоков увеличивает градиент относительной скорости жидкости, приводящий к увеличению гидродинамического сопротивления. При действии одной и той же силы (например, силы тяжести) скорость частиц при совместном падении будет меньше скорости их свободного падения. Чем меньше расстояние между частицами, т. е., чем больше их концентрация, тем меньше будет скорость стесненного падения. В отличие от свободного падения возможны различные скорости стесненного падения в зависимости от концентрации частиц материала.

Условия стесненного падения возникают при падении одиночных частиц в узких камерах, когда размер частиц соизмерим сразмерами камеры, а также при совместном падении однородных и разнородных по размерам, форме и плотности частиц в больших камерах с жидкостью. Для определения скорости стесненного падения частиц рассматриваются две группы формул.

Первая рассматривает совокупность падающих частиц как фильтрационную среду, через которую жидкость протекает в вертикальном направлении снизу вверх.

Вторая представляет стесненное падение как падение отдельной частицы, находящейся в массе других. При этом за основу принимается скорость свободного падения, а условия стесненности учитываются введением в формулы поправочных коэффициентов. Из формул первой группы следует привести

Из формул второй группы наибольшее распространение получила формула Лященко:

где ν_св - скорость свободного падения частиц; λ - показатель степени, зависящий от размера, плотности, формы частиц, а также от соотношения размеров частиц и классификационной камеры.