
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Натуральне число . Властивості натуральних чисел.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одже, поняття про натуральне число розвивалося у двох напрямках. Один напрямок - через безпосереднє встановлення взаємно однозначної відповідності між скінченними множинами. Він привів до поняття натурального числа, як кількісної характеристики певного класу скінченних еквівалентних множин. При цьому натуральне число називається кількісним або кардинальним. Другий напрямок розвитку поняття натурального числа пов’язано з визначенням за допомогою натурального числа місця знаходження елементів будь-якої зчисленної впорядкованої множини. Він привів до поняття порядкового натурального числа, або ординального числа. Відповідно до двох функцій натурального числа існує теоретико-множинна, або кількісна, теорія натурального числа і порядкова, або аксіоматична, теорія. Обидві функції поняття натурального числа тісно пов’язані між собою. При вивченні початкового курсу математики до поняття про натуральне число приходять від поняття про множину. Розглянемо всі еквівалентні між собою скінченні множини А, А1, А2,…Аn. Вважатимемо, що вони утворюють деякий к л а с еквівалентних між собою скінченних множин. Візьмемо далі деяку скінченну множину В, яка не еквівалентна множині А, і утворимо новий клас еквівалентних скінченних множин В, В1, …Вn. Жодна з множин цього класу не ввійде у раніше утворений клас і, навпаки, жодна з множин А, А1, А2,…Аn. не ввійде в клас В, В1, …Вn.. Потужність, або чисельність, скінчених множин є тим спільним, незмінним (інваріантом) всіх скінчених множин деякого класу, що дає змогу, абстрагуючись від конкретності множин, природи їх елементів, об'єднувати всі ці множини в одне — клас. Число, що виражає деяка множина М, називається потужністю множини М і позначається п (М). Число нуль відповідає порожній множині. п (Æ) =0 Означення. Кількісним натуральним числом називається кількісна характеристика деякого класу скінченних еквівалентних між собою множин. Кожному класу еквівалентних скінченних множин відповідає одне і тільки одне кількісне натуральне число і, навпаки, кожному кількісному натуральному числу відповідає один і тільки один клас еквівалентних скінченних множин.. Позначатимемо кількісні натуральні числа відповідними малими буквами латинського алфавіту; тоді цю взаємно однозначну відповідність між кількісними натуральними числами і класами еквівалентних скінчених множин можна зобразити наочно (рис. 1).
Множини, які містять по два елементи, тобто множини, чисельність яких характеризується натуральним числом 2, називаються множинами класу два. Аналогічно вводиться поняття множини класу п. Усі класи еквівалентних скінчених множин утворюють множину класів еквівалентних скінчених множин. Оскільки кожному такому класу відповідає одне і тільки одне натуральне число і, навпаки, кожному натуральному числу відповідає один і тільки один клас еквівалентних скінчених множин, то множина N всіх натуральних чисел буде еквівалентною множині М всіх класів еквівалентних скінчених множин, тобто N ~ М (рис. 2).
Означення. Два натуральних числа а і b називаються рівними тоді і тільки тоді, коли відповідні скінченні множини еквівалентні, і нерівними, коли ці множини не еквівалентні. Тобто а = b тоді і тільки тоді, коли А ~ В. Або А ~ В <=> Сагd (А) = Сагd (В) і а ¹ b тоді і тільки тоді, коли А ~ В, або А ~ В» <=> Сагd (А) ¹ Сагd (В). Оскільки еквівалентні скінченні множини належать до одного класу і їм відповідає те саме натуральне число, то два рівних натуральних числа по суті є тим самим натуральним числом. Оскільки, які б не були скінченні множини А і В або еквівалентні або нееквівалентні, то, які б не були натуральні числа а і b, завжди має місце одне із співвідношень: або а = b, або а ¹ b. Означення. Натуральне число а називається меншим за натурально число b, що позначається а < b, тоді і тільки тоді, коли множина А є власною підмножиною множини В, або А еквівалентна деякій власній підмножині множини В. Тобто а < b, якщо А Ì В або А ~ В', де В' Ì В. Аналогічно а більше b (а > b), якщо В Ì А або В ~ А', де А' Ì А.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.01 с.) |

 Далі замість терміну "кількісне натуральне число" вживатимемо термін «натуральне число». Натурально число 1 характеризує чисельність усіх еквівалентних скінчених множин, які називаються множинами класу один. Це множини, які містять один елемент: множина столиць України; множина коренів рівняння х — 5 = 0 і т.п.
Далі замість терміну "кількісне натуральне число" вживатимемо термін «натуральне число». Натурально число 1 характеризує чисельність усіх еквівалентних скінчених множин, які називаються множинами класу один. Це множини, які містять один елемент: множина столиць України; множина коренів рівняння х — 5 = 0 і т.п. Натуральне число а, будучи інваріантом класу еквівалентних скінченних множин А, А1, А2,…Аn. є разом з тим і характеристикою чисельності кожної з цих множин.
Натуральне число а, будучи інваріантом класу еквівалентних скінченних множин А, А1, А2,…Аn. є разом з тим і характеристикою чисельності кожної з цих множин.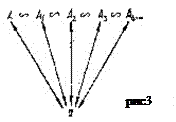 Отже, кожній скінченній множині відповідає одне і тільки одне натуральне число, а кожному натуральному числу відповідає безліч еквівалентних між собою скінченних множин (рис3).
Отже, кожній скінченній множині відповідає одне і тільки одне натуральне число, а кожному натуральному числу відповідає безліч еквівалентних між собою скінченних множин (рис3).


