
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множення цілих невід’ємних чисел. Основні властивості множенняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множення натуральних чисел. Означення множення натуральних чисел можна дати на основі поняття декартового добутку множин. Нагадаємо, що декартовим добутком А X В множини А на В називаєтьея множина всіх впорядкованих пар (a,b) перша компонента яких а наложить множині А: а Î А, а друга b належить множині В: b Î В. Нехай A містить п елементів: А = {a1,a2,…an} а В — т елементів: В = {b1,b2,…bn}. Тоді
п Означення1. Число елементів декартового добутку п-елементноі яножини А на т-елементну множину В називається добутком натурального числа п на натурально число т. інакше, т • п — це сума п натуральних чисел, кожне із яких є т. Візьмемо п скінченних еквівалентних між собою множин без спільних елементів, кожна з яких характеризується кількісним натуральним числом т. 06'єднаємо ці множини в одну множину S, що є їх сумою: S =А1 È А2È А3…È Аn Позначимо кількісне число, що характеризуе множину S, через s;
n доданків Означення 2. Суму n доданків, кожен із яких є m називають добутком натурального числа m на число n. Поняття добутку вводять у другому класі на конкретних множинах. Перед учнями ставлять, наприклад, задачу: «Зошит коштує 2 к. Скільки коштує 9 таких зошитів?» Записавши результат за допомогою суми 2+2+2+2+2+2+2+2+2== 18 (к.), з'ясовують, що такий запис дуже громіздкий і обчислення виконувати довго і незручно навіть при такій, порівняно невеликій, кількості доданків. А що коли б потрібно було визначити вартість 25 зошитів або 75? Тому умовились додавання рівних доданків вважати окремою дією — множенням — і записувати коротше: 2 . 9== 18. Після цього поступово складають таблицю множення (тобто множення одноцифрових чисел), яку діти заучують. Числа при множенні називаються: множене — т, множник — п і добуток —т • п. Результат множення р == т . п також називають добутком. Разом т і п називаються співмножниками, а у початкових класах — просто множниками. Таке означення множення неважко поширити на випадок трьох, чотирьох і більше співмножників. Оскільки доданків не може бути менше ніж два, то добутки т • 1 і т • 0 не мають даного смислу. Адже не можна сказати т взяти доданком 1 раз» або «нуль раз». Тому для цих випадків вводять додаткові означення: а . 1 = а і а . 0 = 0
Дія множення натуральних чисел мае такі властивості: 1. Існування добутку і єдиність добутку. Які б не були натуральш числа а і b, завжди існує єдине натуральне число р, що є їх добутком. ("a, bÎN $!pÎN) ab= p 2. Переставний, або комутативний, закон множення. Добуток двох натуральних чисел не зміниться. якщо переставити співмножники (поміняти їх місцями): ("a, bÎN) (ab= ba) У школі ця властивість розглядаеться у другому класі. На основі неї складається таблиця множення, що дає змогу вдвоє зменшити кількість добутків однозначних чисел, які треба учням запам'ятати. Так, учні замість двох випадків 4 • 3 == 12 і 3 • 4 == 12 запам'ятовують по суті один 4 • 3 == 12. Обгрунтовують цей закон учням на конкретних доцільно підібраних задачах та за допомогою наочної ілюстрації. Задача. Учні посадили біля школи 3 рядки дерев по 4 дерева в кожному. Скільки всього дерев посадили учні?
О О О О О О О О 3 О О О О
Підраховують двома способами: по рядках 4 • 3 == 12, а потім по стовпчиках 3 • 4 = 12. Роблять висновок: 4• 3==3• 4, який після розгляду кількох інших прикладів узагальнюеться. 3 Сполучний, або асоціативний, закон множення. Добуток натуральних чисел не зміниться, якщо будь-які два або кілька співмножників сполучити (об'еднати) і замінити іх добутком. Наприклад, для трьох співмножників ("a, b, сÎN) (abс= (аb)с=а(bс) У початкових класах ця властивють розглядаеться також на конкретних задачах. Задача. Щоб виростити саджанці дуба, діти посадили жолуді. Скільки штук жолудів вони витратили на посадку, якщо в кожну ямку клали по 3 жолуді, а ямки розмістили по 4 у 5 рядочках? Розв'язання задачі виконують двома способами за допомогою наочної ілюстрації. 1. Дізнаються, сюльки жолудів витрачали на один рядок (3 • 4), а потім на 5 рядків: (3•4)•5=60. 2) Дізнаються, сюльки всього ямок (4 • 5), а потім, скільки витрачено жолудів: 3 • (4 • 5) = 60. Аналогічно підраховують кількість учнів у класі, якщо, наприклад, у класі 3 ряди парт, по 5 парт у кожному ряду і за кожною партою сидить по 2 учні: (2 • 5) • 3 = 2 • (5• 3) =30. учиів в всього парт одному ряду Роблять узагальнення. Цей закон разом із комутативним законом множення у початкових класах широко використовують для рацюналізації обчислень. Наприклад:
4. 17 • 25 == (4 • 25) • 17 == 100 • 17 == 1700, 5 • 39 • 2 = 39 • (2 • 5) = 39. 10 = 390.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 848; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.31.251 (0.006 с.) |

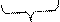 декартів добуток має элементів m+m+…m=m.n
декартів добуток має элементів m+m+…m=m.n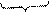 тоді за означениям суми натуральних чисел матимемо s = m+m+…m або s=m.n
тоді за означениям суми натуральних чисел матимемо s = m+m+…m або s=m.n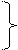 Зобразивши кожне дерево кружечком, дістають схему розміщення посаджених дерев,
Зобразивши кожне дерево кружечком, дістають схему розміщення посаджених дерев,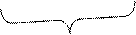 4
4


