Решение уравнений методом простой итерации

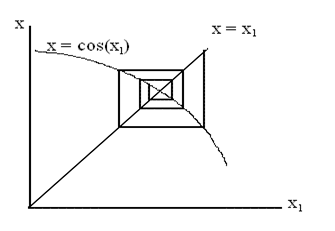
Для решения уравнения f(x)=0 его преобразуют к виду x = f₁(x). Задав некоторое начальное значение корня х = х_н, вычисляют значение f₁(x). Это значение принимают в качестве нового значения корня х. С этим новым значением х вычисляют новое значение функции f₁(x). И так продолжают до тех пор, пока разница между очередными значениями х не станет меньше заданной точности вычисления.

Пример:

Найти корень уравнения x – cos(x) = 0 с точностью E.

Алгоритм решения. Преобразуем наше уравнение к виду x = cos(x). Для пояснения алгоритма введем обозначение х₁ для аргумента функции cos(х₁). Уравнение примет вид x = cos(x₁). Зададим начальное значение х₁ и, подставив его в уравнение, вычислим значение х. Далее приравняем значению х₁ вычисленное значение х. После этого подставим новое значение х₁ в уравнение и вычислим новое значение х. Опять приравняем значению х₁ вычисленное значение х. И снова, подставив новое значение х₁ в уравнение, вычислим новое значение х. Это будем повторять до тех пор, пока различие между очередными значениями х не станут меньше заданной точности E. Тогда полученное значение х и будет корнем заданного уравнения с точностью E.

Поясним физический смысла выполненных нами действий по итерационному решению уравнения рисунком (см. рис. 13).

Рис. 13 Решение уравнения методом простой итерации

Отметим, что решение уравнения таким методом будет найдено, если процедура итерации сходящаяся, т.е. представленная на рис. 13 спираль закручивается в точку, а не раскручивается (в этом случае цикл итераций становится бесконечным). Будет ли процедура такой итерации сходящейся, зависит от вида решаемого уравнения.

Кроме того, скорость решения (число шагов итерации) и сходимость процедуры сильно зависят от того, насколько близко к истинному значению выбрано начальное значение корня уравнения.

CLS

INPUT “Введите точность”, E

INPUT “Введите начальное значение х”, х

DO

х1 = x

x = cos(x1)

LOOP WHILE ABS(x - x1) > E

PRINT”Корень уравнения х=”; x

END

Если оставить программу в таком виде, то, в принципе, ею будет решаться задача вычисления корня, но не будет грамотного отображения результатов решения задачи.

Кроме того, текст программы должен быть структурирован и содержать комментарии.

Для программирования необходимой формы отображения результатов решения задачи, необходимо сначала спроектировать эту форму. Отметим, что проектирование и программирование формы выдачи результатов расчета является обязательной составной частью решения любой задачи вычислений на компьютере.

Форма выдачи результатов решения обычно должна содержать три раздела: исходные данные, ход решения и собственно ответ на поставленную задачу. В нашем примере эта форма может иметь, например, такой вид (рамка дана, чтобы выделить форму в тексте, не для программы).

Исходные данные: начальное значение х = …, точность ….

№ итерации Значение корня

1 …

2 …

3 …

……………………………

Полученное значение корня уравнения х = …….

 

 

С учетом спроектированной формы выдачи результатов, применяя структурирование текста программы (т.е. делая отступы содержимого циклов, а также отступы для операторов внутри связки DO … LOOP WHILE) и включая комментарии, перепишем нашу программу в виде:

 

 

CLS

REM Метод простой итерации

INPUT “Введите точность”, E

INPUT “Введите начальное значение х”, х

CLS

PRINT “Исходные данные: начальное значение х =”; x; “, точность ”; E

PRINT

PRINT TAB(11); “№ итерации Значение корня”

N=0

DO

N=N+1

х1 = x

x = cos(x1)

PRINT TAB(18); N; TAB(28); x

LOOP WHILE ABS(x - x1) > E

PRINT

PRINT”Корень уравнения х=”; x

END

Итерационное решение уравнений методом половинного деления

Пусть f(x) на концах отрезка принимает значения разного знака. Вычислим значение функции в середине этого отрезка и посмотрим его знак. Знак будет отличаться от знака функции на одном из концов отрезка, но совпадать со знаком на другом конце. Продолжая действовать тем же образом, мы можем получить сколь угодно малый отрезок, причем известно, что корень уравнения лежит на этом отрезке. Так определяют корень с любой нужной точностью. Новая программа не намного сложнее, но результат получается быстрее.

CLS

DECLARE FUNCTION F (x AS DUBLE)

INPUT “Введите точность”, E

x1 = 0

x0 = 1

y0 = F(x0)

y1 = F(x1)

DO

x2 =.5*(x1 + x0)

y2 = F(x2)

IF SGH(y2) = SGH(y0) THEN

x0 = x2

y0 = y2

ELSE

x1 = x2

y1 = y2

END IF

PRINT x1, x0

LOOP WHILE ABS(x1-x0) > E

FUNCTION F (x AS DUBLE)

F = x - cos(x)

END FUNCTION

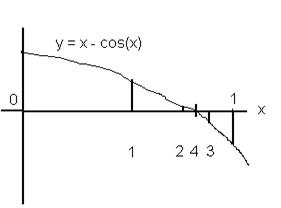
1,2,3,4 – точки деления

Рис. 14 Решение уравнения методом простой итерации