
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические отношения между простыми суждениямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим вопрос о логических отношениях между категорическими суждениями. Логические отношения – это отношения между суждениями по их логической форме, то есть в отвлечении от их конкретного содержания (от того, о чем конкретно идет в них речь – о космонавтах или юристах, об атомах или пресмыкающих и т.п.). Это отвлечение (абстрагирование) производится заменой входящих в суждения понятий (дескриптивных терминов) логическими параметрами P, Q, R, S и т.п., так что после этого остается лишь схема («скелет») этого суждения. К примеру, заменяя в суждении «Все киты – млекопитающие животные» дескриптивные (описательные) термины «кит» и «млекопитающее животное» на параметры Q и R, получаем запись логической формы этого суждения: «Все Q суть R». Понятно, что сходную логическую структуру имеют и многие другие суждения, чье конкретное содержание отличается от вышеприведенного, например, «Все судьи – юристы», «Все металлы – электропроводные вещества» и т.д. Для чего необходимо в логике отвлечение от конкретного содержания суждений? Дело в том, что одна из главнейших задач этой науки – описание общих условий правильности умозаключений (выводов). Уже Аристотель доказал, что правильность дедуктивных умозаключений не зависит от конкретного содержания входящих в их состав посылок и заключения: она определяется исключительно логической формой этих суждений. Так, умозаключение «Киты – млекопитающие животные (Все Q суть R), а у млекопитающих нет жабр (Все R не суть P); следовательно, у китов тоже нет жабр (Все Q не суть P)» является правильным. Но правильным является и умозаключение «Ель – растение, а у растений нет рефлексов; значит и у ели нет рефлексов», хотя схема этого умозаключения в точности такая, как и первого: «Все Q суть R; Все R не суть P; следовательно, Все Q не суть P». Логические отношения между категорическими суждениями удобно иллюстрировать на схеме, именуемой логическим квадратом:
Отметим, что этой схемой иллюстрируются только отношения между сравнимыми суждениями, т.е. попарно взятыми суждениями, у которых одинаковые субъекты и предикаты. Символы a, e, i, o обозначают выделенные нами ранее логические типы суждений (соответственно: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные). Верхняя горизонталь (а ↔ е) символизирует отношение контрарности (противоположности), нижняя (i ↔ o) – отношение субконтрарности, левая вертикаль (a → i) и правая вертикаль (е → о) – отношение логического подчинения, а диагонали (а ↔ о) и (е ↔ i) – отношения контрадикторности (логического противоречия). Двойные стрелки указывают, что отношение обратимое (например, а контрарно е, и е контрарно а), а стрелки → указывают однонаправленность отношения ·Суждения X и Y находятся в отношении контрарности, когда они несовместимы по истине (т.е. не могут быть одновременно истинны), но совместимы по ложности (могут быть оба ложными). Возможен также вариант, когда одно из них – истинное суждение, а другое – ложное (или наоборот). Рассмотрим примеры контрарных суждений. Среди категорических суждений в этом отношении находятся суждения типа а и е. Так, контрарными являются суждения: - Все лебеди белые птицы (а) - Все лебеди не являются белыми птицами (т.е. ни один лебедь не Как известно, оба эти суждения – ложные. Но контрарными являются и суждения: - Все металлы – электропроводны. - Все металлы не являются электропроводными. Здесь первое суждение ( типа а) – истинно, а второе (е) – ложно. Таким образом, для контрарных суждений из четырех возможных вариантов распределения их истинностных значений исключен только первый: они не могут быть оба истинными, т.е. они несовместимы по истине:
·Суждения X и Y находятся в отношении контрадикторности, когда они несовместимы как по истине, так и по лжи:
– Все преступники опасны для общества (а) – Некоторые преступники не опасны для общества (о) Как известно, истинным является первое суждение, а второе - ложно. Второй пример: – Некоторые металлы – жидкости (i) – Все металлы не являются жидкостями (е) В этом случае истинно частное суждение, а ложно общее. ·Суждения X и Y находятся в отношении субконтрарности, когда они не могут быть оба ложными (т.е. они несовместимы по ложности, но совместимы по истине). Это означает, что из четырех возможных вариантов распределения значений истинности исключен только один: Х – ложь и Y – ложь (они несовместимы по ложности):
В сфере категорических суждений в этом отношении находятся суждения i и о. · Суждение Х логически подчиняет суждение Y, когда при истинности Х истинно и Y, а при ложности Y ложно Х. В отношении логического подчинения находятся попарно взятые категорические суждения a, i и e, o: это означает, что истинность общего суждения гарантирует истинность частного, а ложность частного исключает истинность общего. Примеры: при истинности суждения Все рыбы дышат жабрами нет оснований сомневаться в истинности суждения Некоторые рыбы дышат жабрами, поскольку информация, содержащаяся во втором из этих суждений, составляет часть информации первого: раз все рыбы такие, то и некоторые таковы, то есть существует, по меньшей мере, одна рыба, которая дышит жабрами. Отношение логического подчинения необратимо: истинность частного суждения не гарантирует истинность общего. Так, истинность суждения Некоторые юристы – следователи никак не влияет на значение истинности общего суждения Все юристы – следователи (последнее ложно). Между тем, ложность частного суждения «Некоторые четные числа не делятся на 2» однозначно свидетельствует о ложности общего суждения Все четные числа не делятся на 2. * * * В теме 1. уже речь шла о законе противоречия и законе исключенного третьего. Первый закон был сформулирован так: Неверно, что Х и не- Х Применительно к категорическим суждениям мы имеем следующие формулировки этого закона: Неверно, что Все S суть P и Некоторые Sне суть P Неверно, что Все S не суть P и Некоторые Sсуть P Закон исключенного третьего формулировался нами так: Х или не- Х В области категорических суждений мы имеем такие его формулировки: Все S суть P или Некоторые Sне суть P Все S не суть P или Некоторые Sсуть P
* * * Обратите внимание! Не каждая пара сравнимых суждений Практикум
1. Используя логический квадрат, сформулируйте суждения, противоположные, противоречащие и подчиненные данным. 1) Ни одно млекопитающее не живет в воде. 2) Все адвокаты – юристы. 3) Среди взяточников нет честных людей. *Прежде чем выполнить упражнение, вспомните, что собой представляет каждое из логических отношений. Так, отношение подчинения связывает общие и частные высказывания, одинаковые по качеству: а и i, e и o. Суждение i (o) подчинено суждению a (e), а это означает, что при истинности общего суждения частное тоже является истинным, а ложность частного суждения с необходимостью влечет ложность общего. В двух других возможных случаях (исходная истинность частного или ложность общего высказывания) нельзя получить логически необходимый вывод об истинностном значении второго суждения (такое положение называется логической неопределенностью). Например: Все птицы к зиме улетают в теплые края. Суждение – Подчиненным этому суждению является суждение типа i: Некоторые птицы к зиме улетают в теплые края. Ложность общего высказывания обусловливает логическую неопределенность частного. Поэтому необходимо обратиться к содержанию частноутвердительного суждения: то, что некоторые птицы улетают в теплые края, соответствует действительности, т.е. оно истинно. – Противоположным исходному является суждение типа e: Ни одна птица к зиме не улетает в теплые края. Суждения а и e – противоположны, и это означает, что они несовместимы по истинности. Но в данном примере суждение типа а – ложно, поэтому контрарное ему суждение типа e – логически неопределенно. Обращаемся к содержанию нашего суждения e: утверждение, что нет таких птиц, которые улетают в теплые края, не соответствует действительности. Значит, это суждение по факту ложно. – Противоречащим исходному будет суждение о: Некоторые птицы к зиме не улетают в теплые края. Отношение противоречия означает несовместимость суждений как по истинности, так и по ложности. Исходное наше суждение типа а – ложно, следовательно, суждение типа о будет истинным. Действительно, суждение «Некоторые птицы к зиме не улетают в теплые края» соответствует реальному положению дел. 2. Сформулируйте категорические суждения, противоречащие, подчиняющие либо подчиненные данным, а также – если это возможно – противоположные данными: а) Люди здесь все обходительные. б) Некоторые люди неграмотны. 3. Установите, какие из следующих пар суждений находятся в отношении логического противоречия: · Ничто не ново под луной. – В подлунном мире иногда происходит что-то новое. · На всякого мудреца довольно простоты. – На этого мудреца тоже хватило простоты. · Некоторые стихотворения Пушкина написаны четырехстопным ямбом. – Ни одно стихотворение Пушкина не написано четырехстопным ямбом.
3.4. Логическая форма и виды
Сложные суждения образуются из других суждений посредством установления логических связей между ними. Рассмотрим эти связи. · КОНЪЮНКТИВНАЯ СВЯЗЬ. В естественном языке выражается с помощью союза «и», соединяющего попарно взятые суждения. Возникающие таким образом сложные суждения именуются соединительными, или конъюнктивными, а связь между их составляющими – конъюнкцией. Пример конъюнктивной связи между суждениями: Джейн вышла замуж и у нее родился ребенок. Заменим суждение Джейн вышла замуж параметром Х, а суждение У нее родился ребенок – параметром Y. Получаем логическую форму (формулу)этого сложного суждения: «X и Y», что позволило нам отвлечься от конкретного содержания этого суждения. В естественном языке связь суждений посредством союза «и» не всегда «прозрачна», имеет несколько смысловых оттенков. Выражения вроде «Х, но и Y», «Х, несмотря на Y», «Х, хотя и Y» как раз и содержат эти различия, но при их записи в логическом языке они исчезают. Конъюнктивное суждение является истинным при одном условии: истинно и суждение Х, и суждение Y (во всех остальных случаях оно является ложным):
· ДИЗЪЮНКТИВНАЯ СВЯЗЬ. В естественном языке выражается с помощью союза «или». Образующееся сложное суждение называется разделительным, или дизъюнктивным, а сама связь – дизъюнкцией. Пример: Пожар возник по причине неисправности электропроводки или неосторожности обращения с огнем. В отношении этого союза в обыденной речи также есть сложности: его нередко путают с другим, существенно отличающимся по роли в мышлении союзом, хотя само слово используется то же (к примеру, в предложении Петр спит или читает газету). Для различения этих двух связей первую назовем нестрогой, и логическую форму суждения с таким союзом представлять в виде формулы «X или Y». Дизъюнктивное суждение с нестрогой дизъюнкцией ложно при одном условии: ложно и суждение Х, и суждение Y (во всех остальных случаях оно является истинным):
Вторую дизъюнктивную связь назовем строгой дизъюнкцией, и логическую формулу соответствующего суждения (второй пример) будем представлять в виде формулы«X либо Y». Дизъюнктивное суждение со строгой дизъюнкцией истинно при одном условии: одно, и только одно, из суждений – Х либо Y – должно быть ложным (во всех остальных случаях оно является ложным):
где знак « Посредством строгой дизъюнкции мышление воспроизводит факт несовместимости некоторых ситуаций (событий), как, например, это имеет место в суждении Подброшенная монета выпадет орлом либо решкой. Дизъюнктивные суждения уместны там, где перечисляются возможные варианты исхода каких-либо событий, перечня альтернативных решений. · ИМПЛИКАТИВНАЯ СВЯЗЬ. В естественном языке ее представляет выражение «Если, то» или равнозначные ему «Тогда, когда», «В случае», и др. Образующееся с его участием сложное суждение «Если Х, то Y» называют условным, или импликативным. Примеры такого вида суждений: «Если отсутствует состав преступления, то уголовное дело не может быть возбуждено» \ Когда сверкает молния, гремит гром \ В случае снегопада движение по дороге затруднено. Левую часть импликативного суждения будем называть основанием, а правую – следствием. Импликативное суждение ложно при одном условии: когда его основание Х истинно, а следствие Y ложно (во всех остальных случаях оно является истинным):
С помощью импликативных суждений можно представить любые условные зависимости, включая и причинные (Если по проводнику течет ток, то вокруг него образуется электромагнитное поле). Условная связь «если, то» позволяет уточнить важное для научного и профессионального мышления понятие достаточного условия чего-либо. Обстоятельство (ситуация) Х является достаточным условием обстоятельства Y, если всегда, когда имеется Х, имеется и Y. Обстоятельство (ситуация) Х является необходимым условием, если при отсутствии Х отсутствует и обстоятельство Y. Совершение убийства каким-либо человеком не является достаточным условием признания его преступником (скажем, в случае, если этот человек в момент совершения этого деяния был невменяем по независящим от него обстоятельствам). А незаконное хранение оружия достаточно для привлечения к уголовной ответственности, хотя оно не является необходимым для этого (привлечь к уголовной ответственности можно по другой причине, например, за хищение чужого имущества). Активное участие общественности в ликвидации преступности является необходимым, но недостаточным ее условием. · ЭКВИВАЛЕНТНАЯ СВЯЗЬ. В естественном языке эта связь воспроизводится выражениями «Х, если и только если Y», «Х только тогда, когда Y», «Если Х, то Y, и если Y, то Х», «Y равносильно Х». Примеры эквивалентной зависимости суждений: Некоторое число делится на 6, если и только если оно делится на 2 и на 3 \ Обвиняемый может быть назван преступником, если и только если его деяния признаны судом уголовно наказуемыми. Суждение эквивалентности ложно при ложности одного, и только одного, из суждений Х, Y (во всех остальных случаях оно является истинным):
В суждении эквивалентности формулируется необходимое и достаточное условие какого-либо обстоятельства, к примеру, наступления правовой ответственности. Убийство признается совершенным группой лиц, е.т.е. в его совершении совместно участвовали два или более исполнителя. В этом высказывании участие двух или более исполнителей в совершении убийства признается и достаточным, и необходимым условием истинности суждения. Такое убийство квалифицируется как совершенное группой лиц. * * *
«Перевод» сложных суждений на логический язык позволяет однозначным и наглядным образом выявить логическую форму сложных суждений и, тем самым, уточнить в целом их содержание. Рассмотрим сложное суждение При совершении клеветы умысел виновного направлен на унижение чести и достоинства потерпевшего, а не на привлечение его к уголовной ответственности. Внимательное прочтение текста подскажет нам, что в целом он выражает условное (импликативное) суждение: Если виновный совершил клевету в отношении потерпевшего, то умысел виновного направлен на унижение чести и достоинства потерпевшего, и неверно, что этот умысел направлен на привлечение его к уголовной ответственности. Главным логическим союзом всего этого суждения является импликация «если, то ». Следствие этого суждения является, в свою очередь, сложным суждением, составленным из простых посредством логической связки «неверно, что». Произведем замену простых предложений «Виновный совершил клевету в отношении потерпевшего», «Умысел виновного направлен на унижение чести и достоинства потерпевшего», «Этот умысел направлен на привлечение его к уголовной ответственности» параметрами х, y, z. Логическая форма анализируемого суждения будет такова: Если х, то (y и неверно, что z) Чтобы точнее представить структуру формулы логического языка, мы воспользовались левой и правой скобками. Они указывают, какой из логических союзов в сложном суждении является главным. В нашем примере таковым является союз «Если, то». Перевод» суждений с естественного языка на логический далеко не механическая процедура. Однако после выполнения нескольких упражнений по такому переводу соответствующий навык вполне можно приобрести.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 904; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |


 1) и и
1) и и 2) и л
2) и л 3) л и
3) л и 1) и и
1) и и 2) и л
2) и л 2) и л
2) и л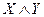
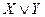
 » – обозначение нестрогой дизъюнкции, а знак «
» – обозначение нестрогой дизъюнкции, а знак « » – строгой.
» – строгой.



