
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура простого категорического силлогизмаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Простым категорическим силлогизмом (сокращенно: ПКС) называется умозаключение, в котором в качестве посылок выступают два категорических суждения. Заключением в нем также является категорическое суждение, в котором содержатся понятия (термины), каждое из которых встречается только в одной посылке. В каждой из посылок имеется еще одно одинаковое для них понятие (термин), которое отсутствует в заключении. Понятие, общее для обеих посылок, называется средним термином. Понятие, выступающее в роли предиката заключения, именуют большим термином; понятие, которое играет роль субъекта заключения, называют меньшим термином. Больший и меньший термины называют крайними. Больший термин содержит большая посылка, меньший термин содержит меньшая посылка. В стандартно построенном силлогизме большая посылка должна стоять первой. В силлогизме 1. Все млекопитающие (М) – теплокровные (Р) (I) 2. Все тюлени (S) – млекопитающие (М)
понятие «тюлень» – субъект (S) заключения (меньший термин); «теплокровный» – его предикат (Р) (больший термин); «млекопитающие» – средний термин (М); большая посылка – первая, меньшая – вторая. Силлогистика (учение о силлогизмах) описывает схемы умозаключений, которыми можно пользоваться как правилами вывода. Пример схемы простого силлогизма: МаР (II) SаМ
Данная запись является схемой приведенного выше силлогизма (I). Переход от посылок к заключению в силлогизме связан с ролью среднего термина: отношение субъекта S и предиката Р в заключении опосредуется средним термином М, т.е устанавливается в зависимости от их отношения к среднему терминув посылках. Рассмотрим для примера схему (II). Здесь первая (большая) посылка содержит утверждение о том, что все предметы множества М включаются во множество Р. В свою очередь, вторая (меньшая) посылка указывает, что все предметы множества S включаются во множество М. Графически эти соотношения могут быть представлены так:
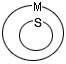
Теперь совместим обе посылки:
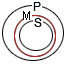
Хорошо видно, что все предметы множества S оказываются также элементами множества Р, а именно это обстоятельство констатируется в заключении SаР рассматриваемой схемы.
Практикум
1. Найдите заключение и посылки в следующих силлогизмах: а) Некоторые морские животные – млекопитающие, ведь все киты – морские животные, и все они – млекопитающие. б) В каждом квадрате диагонали взаимно перпендикулярны, и поскольку они перпендикулярны в каждом ромбе, все квадраты – ромбы. *Пример. Ни один скупой человек не счастлив, ибо он вечно не доволен собой, тогда как всякий счастливый человек всегда собой доволен. Суждение Ни один скупой человек не счастлив – это заключение. Далее идет его обоснование, на что указывает союз «ибо». Таким образом: меньшая посылка: Все скупые люди вечно не довольны собой, большая посылка: Всякий счастливый человек всегда собой доволен. 2. Сделайте разбор структуры нижеприведенных ПКС: в каждом из них найдите заключение, затем больший, меньший и средний термины, большую и меньшую посылки. Изобразите отношения между терминами в посылках и заключении с помощью круговых схем. а) Все рыбы дышат жабрами. Значит, кит – не рыба, ведь он не дышит жабрами. б) Электрон имеет отрицательный заряд. Электрон – элементарная частица. Следовательно, некоторые элементарные частицы имеют отрицательный заряд. в) Тополь поглощает углекислоту, ибо тополь – растение, а все растения поглощают углекислоту. *Пример. Люди грешны. Следовательно, короли грешны, так как они люди. Все суждения в этом умозаключении – общие, хотя явно это не выражено (в естественном языке это допускается). Заключением является стоящее после слова «следовательно» суждение Все короли грешны. Термин «короли» – меньший термин, так как является субъектом S заключения, термин «грешны» – больший термин, поскольку является предикатом Р заключения. Суждение Все люди грешны – большая посылка, потому что содержит предикат Р заключения, а суждение Все короли грешны – меньшая, поскольку содержит субъект S заключения. Средний термин М – «люди», содержащийся в каждой посылке Отношение терминов по их объему таково:
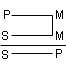
3. Определите, относится ли нижеследующее умозаключение к ПКС: Кто курит, тот вредит своему здоровью. Значит, среди тех, кто вредит своему здоровью, есть и те, кто курит. 4.2.4.2. Фигуры и модусы простого Существует четыре возможных варианта расположения среднего термина в посылках и, соответственно, четыре конструкции или, как их называют, фигуры силлогизма: 1) средний термин является субъектом в большей посылке и предикатом в меньшей (первая фигура); 2) средний термин является предикатом в обеих посылках (вторая фигура); 3) средний термин является субъектом в обеих посылках (третья фигура); 4) средний термин является предикатом в большей посылке и субъектом в меньшей (четвертая фигура). Названные фигуры схематически изображаются так:
Примером умозаключения по первой фигуре может послужить приведенный в разделе 4.2.4.1 вывод (I) (про тюленей). А вот пример умозаключения по второй фигуре: 1. Все юристы (Р) – дипломированные специалисты (М). 2. 3. Некоторые правозащитники (S) не являются юристами (Р). Пример умозаключения по третьей фигуре: 1. Все допросы обвиняемого (М) оформляются протоколом (Р). 2. Все допросы обвиняемого (М) – следственные действия (S). 3. По четвертой фигуре протекает следующее умозаключение: 1. Все судебные приставы (Р) – чуткие люди (М). 2. 3. Ни один злой человек (S) не является судебным приставом (Р). В каждой фигуре силлогизма возможны варианты – их называют модусами. Модусы фигуры отличаются друг от друга качественной и/или количественной характеристиками входящих в них суждений. Так, модусами первой фигуры являются (среди прочих других) схемы MaP MеP MaP SaM SiM SiM
Количество модусов у каждой фигуры – 64, а всего модусов четырех фигур насчитывается 256. Однако большинство из них не являются правильными, поскольку могут приводить от истинных посылок к ложному заключению. Неправильным, к примеру, является модус первой фигуры:
1. Ни один летчик (М) не является незрячим (Р) 2. Некоторые космонавты (S) – летчики (М) 3. Хотя посылки этого умозаключения – истинные суждения, его заключение ложно. Для запоминания правильных модусов каждой фигуры в традиционной логике им приписывались соответствующим образом сконструированные названия, указывающие на структуру (строение) модуса. Так, четвертый модус первой фигуры MeP SiM
носит название Ferio. Трем гласным буквам этого слова e, i, o соответствуют типы категорических суждений, входящих в посылки и заключение этого умозаключения. Приведем перечень названий правильных модусов каждой из фигур:
4.2.4.3. Методы логического анализа Первый способ основан на установлении фигуры и модуса анализируемого силлогизма. ·Сначала установим, относится ли данное умозаключение к простому категорическому силлогизму: выделим его посылки (их должно быть в точности две) и заключение; все посылки и заключение должны быть категорическими суждениями; в умозаключении должно быть в точности три разных термина. ·Строим формальную схему этого умозаключения. На первом месте в схеме вывода любого ПКС всегда должна находиться большая посылка. Указываем распределенность его терминов. К примеру, это будет схема Р + аМ –
S – iP – ·Устанавливаем фигуру и модус анализируемого силлогизма, а затем определяем, имеется ли такая схема вывода в числе правильных модусов данной фигуры. В нашем примере: эта схема относится к правильному модусу а, а, i четвертой фигуры. Второй способ связан с использованием общих правил простого категорического силлогизма. Сформулируем их: Правила посылок 1. Из двух отрицательных посылок нельзя получить заключения (по крайней мере одна из посылок должна быть утвердительной). 2. Если в выводе есть отрицательная посылка – заключение должно быть отрицательным. 3. Если обе посылки – положительные (утвердительные) суждения, заключение должно быть положительным. 4. Из двух частных посылок нельзя получить заключения (одна из посылок должна быть общим суждением). 5. Если среди посылок есть частное суждение, заключение тоже должно быть частным. Правила терминов 6. Средний термин должен быть распределен хотя бы в одной из посылок. 7. Термин, который не распределен в посылке, не должен быть распределен в заключении. В приведенной выше схеме умозаключения (I)ни одно правило посылок не нарушено: правила 1., 2., 4. и 5. вообще не относятся к данной схеме, а правила 3., 6., 7. соблюдены; следовательно, любое умозаключение, построенное по данной схеме, является корректным. Третий способ решения вопроса о корректности силлогистического умозаключения – построение круговых схем. Возьмем в качестве примера схему вывода РаМ (II) МаS
Первая посылка утверждает, что каждое Р есть М. Пусть меньший круг символизирует множество всех предметов Р, а больший круг – множество всех предметов М. Тогда отношение объемов понятий (терминов) Р и М графически представимо следующим рисунком:
Вторая посылка утверждает, что все М есть S. Отметим это обстоятельство включением круга М в более широкий круг S:
Из последнего рисунка видно, во-первых, что некоторые предметы типа S действительно относятся к множеству Р (это означает истинность заключения «Некоторые S есть Р»), а во-вторых, что истинность этого заключения однозначно определена соотношением объемов крайних терминов Р и S со средним в посылках. Теперь установим некорректностьумозаключения Некоторые юристы (М) – адвокаты (Р). Некоторые депутаты (S)- юристы (М).
По списку правильных модусов первой фигуры в их перечне нет модуса i,i,i. Обратимся к общим правилам ПКС: нарушены правила 4., 5. и 6.. Наконец, проведем анализ с помощью круговых схем. Круговая схема

адекватно воспроизводит отношения крайних терминов к среднему в посылках рассматриваемого умозаключения, но не соответствует их отношению друг к другу в заключении.
* * * В практике юридического мышления часто встречаются двухпосылочные дедуктивные умозаключения, одна из посылок которых – единичное суждение, а другая – общее суждение. К примеру: Ни один невиновный не должен быть осужден. Сократ был невиновен.
Учитывая, что в единичном суждении субъект распределен (поскольку является единичным именем), а в отрицательном распределен предикат, ранее мы приняли следующие соглашения: ·Единичное утвердительное суждение приравнивается (по своей логической форме) к общеутвердительному. ·Единичное отрицательное суждение приравнивается к общеотрицательному. В связи с этим соглашением формальная схема анализируемого умозаключения примет следующий вид: МеР SаМ 1-я фигура, модус Celarent
Данный подход позволит нам более широко и продуктивно использовать правила и схемы простого категорического силлогизма. В мышлении первая фигура простого категорического силлогизма часто используется в качестве логического средства квалифицирования, суть которого в юриспруденции состоит в подведении социально значимого деяния (либо его конкретного случая) под определенную правовую норму либо оценку (см. раздел 5.5 .). Преступление – уголовно наказуемое деяние. Дача взятки – преступление. Следовательно, дача взятки – уголовно наказуемое деяние. В этом силлогистическом выводе с помощью схемы МаР SаМ 1-я фигура, модус Barbara
дача взятки квалифицируется как уголовно наказуемое деяние. Вторая фигура в юриспруденции используется как средство опровержения неправильной правовой квалификации. Самовольный уход из воинской части является преступлением. Уход из воинской части №19055 рядового Кроткова по увольнительной не является преступлением. Следовательно, уход Кроткова из воинской части по увольнительной не является самовольным уходом. Данное умозаключение построено по схеме РаМ SеМ 2-я фигура, модус Camestres
которая и составляет логическую основу опровержения квалификации ухода из воинской части по увольнительной как ее самовольного оставления. Третья фигура может быть использована в качестве логического средства опровержения необоснованных обобщений. К примеру, необоснованность суждения Ни один аморальный поступок не является преступлением следует из заключения вывода, в котором все посылки – истинные суждения: 1. Любая кража – преступление. 2. Любая кража – аморальный поступок.
Формальная схема этого вывода МаР МаS
является правильным модусом третьей фигуры. Учитывая, что суждение SiP находится в отношении противоречия с суждением SеP, по схеме непосредственного вывода по «логическому квадрату» получаем: Неверно, что ни один аморальный поступок не является преступлением Четвертая фигурав мышлении используется редко.
Практикум
1. Проверьте корректность силлогизмов по общим правилам: а) Каждый учебник – полезная книга, так как он несет информацию, а всякая полезная книга несет информацию. б) Все учащиеся, пропускающие занятия, испытывают трудности при сдаче экзаменов. Но поскольку некоторые студенты не являются такими учащимися, они не испытывают трудностей при сдаче экзаменов. в) Все металлы имеют определенную температуру плавления, так как все кристаллические вещества имеют определенную температуру плавления, а некоторые кристаллические вещества – металлы. г) Большинство продаваемых теперь книг – детективы, тогда как большинство высокохудожественных книг к этому жанру не относятся. Значит, большинство продаваемых теперь книг не являются высокохудожественными. 2. Проверьте на круговых схемах корректность следующих силлогизмов: а) Некоторые студенты работают, и многие студенты хорошо учатся. Значит, некоторые из хорошо учащихся – работают. б) Все обитатели этого аквариума – рыбы, а все рыбы не имеют легких. Значит, ни одно имеющее легкие животное не обитает в этом аквариуме. в) Все растения вырабатывают при дыхании кислород. Все вырабатывающие при дыхании кислород организмы полезны. Значит, некоторые полезные организмы не растения. г) Все великие поэты – одаренные личности, значит и А.С. Пушкин был одаренной личностью, поскольку он – великий поэт. *Пример: 1. Каждый гражданин РФ имеет право на образование. 2. Николаев – гражданин РФ.
Находим субъект и предикат в заключении: «Николаев» – S, «имеющий право на образование» – Р. Средним термином М является «гражданин РФ». Первая посылка содержит больший термин Р, значит, это большая посылка. Вторая посылка, содержащая термин S – меньшая посылка. Логическая форма силлогизма: MaP SaM
Соотношение терминов по объему таково:
Из этой схемы видно, что при истинности посылок заключение также истинно. 3. Являются ли нижеследующие схемы выводов правильными модусами простого категорического силлогизма? Проверьте, не нарушены ли в них какие-либо правила силлогизма?
4.Укажите, какое заключение дедуктивно выводимо из посылок?
4.2.4.4. Сокращенный категорический силлогизм. Силлогистические умозаключения широко используются в юридическом мышлении, особенно в ходе различного рода судебных разбирательств (дискуссий). В этих процессах обычно фигурируют сокращенные формы силлогизмов, которые именуются энтимемами. Слово «энтимема» в переводе с греческого означает «в уме». Энтимема –это простой категорический силлогизм, в котором не выражена явно, но подразумевается либо одна из посылок, либо заключение. Различают три вида энтимемы: 1) Силлогизм с пропущенной большей посылкой (Трифонов – судья областного суда. Следовательно, он юрист. Пропущена, но подразумевается посылка Все судьи областных судов – юристы). 2) Силлогизм с пропущенной меньшей посылкой (Все судьи областных судов – юристы. Следовательно, Трифонов – юрист. Подразумевается посылка Трифонов – судья областного суда). 3) Силлогизм с пропущенным заключением (Все судьи областных судов – юристы, а Трифонов – судья областного суда. Не сформулировано заключение Трифонов – юрист). Мыслить энтимемами более экономично. Однако недостающее их звено может оказаться ложным либо спорным суждением, что не всегда удается «уловить» в силу его невыраженности в речи. Поэтому в подобных случаях полезно восстановить недостающую посылку или несформулированное явно заключение. Сформулируем некоторые правила (вытекающие из общих правил категорического силлогизма), позволяющие восстановить недостающие части силлогизма: п.1. Если дана одна из посылок и заключение, то недостающая посылка должна быть суждением, из которого совместно с имеющейся посылкой дедуктивно выводимо заключение.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.81.172 (0.013 с.) |


 3. Все тюлени (S) – теплокровные (Р)
3. Все тюлени (S) – теплокровные (Р) SаР
SаР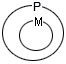




 Некоторые правозащитники (S) не являются дипломированными специалистами (М).
Некоторые правозащитники (S) не являются дипломированными специалистами (М). Некоторые следственные действия (S) оформляются протоколом (Р).
Некоторые следственные действия (S) оформляются протоколом (Р). Ни один чуткий человек (М) не является злым (S).
Ни один чуткий человек (М) не является злым (S).

 SaP SoPSiP
SaP SoPSiP Некоторые космонавты (S) – незрячие (Р)
Некоторые космонавты (S) – незрячие (Р) SoP
SoP (I) М + аS –
(I) М + аS –

 Некоторые депутаты (S) – адвокаты (Р).
Некоторые депутаты (S) – адвокаты (Р).

 Сократ не должен быть осужден.
Сократ не должен быть осужден. SaP
SaP SеP
SеP 3. Некоторые аморальные поступки являются преступлением.
3. Некоторые аморальные поступки являются преступлением. SiP
SiP 3. Николаев имеет право на образование.
3. Николаев имеет право на образование.
 SoP
SoP
 SaM
?
SaM
?
 SaM
?
SaM
?



