Таблицы, схемы и логические правила

Модальные суждения: эквивалентности

Необходимо, что x ≡ Неверно, что возможно не- x

Случайно, что x ≡ Возможно, что x, и возможно, что не- x

Неверно, что необходимо x ≡ Возможно, что не- x

Неверно, что запрещено x ≡ Разрешено x

* * *

Обязательно, что x ≡ Неверно, что возможно не- x

Запрещено, что x ≡ Обязательно, что не- x

Неверно, что запрещено x ≡ Разрешено x

 

* * *

 

Доказано, что x ≡ Неверно, что правдоподобно не- x

Доказано, что не- х ≡ Опровергнуто, что x

Правдоподобно, что x ≡ Неверно, что доказано x, и неверно, что опровергнуто x

Если доказано, что x, то x имеет место

Если опровергнуто, что x, то x не имеет места

 

Категорические суждения

 

Названия видов категорических суждений	Логические формы (стандартные формулы) суждений	Отношения терминов (S и P)
Общеутвердительные (Сокращенно: суждения типа а)	Все S суть P (Сокращенно: SaP)
Общеотрицательные (суждения типа е)	Все S не суть P (SeP)
Частноутвердительные (суждения типа i)	Некоторые S суть P (SiP)
Частноотрицательные (суждения типа о)	Некоторые S не суть P (SoP)

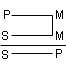
Логический квадрат

 

 

 

Внешнее отрицание: эквивалентности

 

(1) Неверно, что (Все S суть P) ≡ Некоторые S не суть P.

(2) Неверно, что (Все S не суть P) ≡ Некоторые S суть P

(3) Неверно, что (Некоторые S суть P) ≡ Все S не суть P

(4) Неверно, что (Некоторые S не суть P) ≡ Все S суть P

 

Дедуктивные правила вывода
из сложных суждений

модус поненс МП:

Если Х, то Y; Х

Y

модус толленс МТ:

Если Х, то Y; не- Y

Не-Х

 

 

первое правило исключения дизъюнкции ИД₁:

X или Y; не- X

Y

 

второе правило исключения дизъюнкции ИД₂:

 

Х либо Y; Y

Не-X

правило исключения двойного отрицания ИО:

Неверно, что не-Х

Х

 

правилотранзитивности ПТ:

 

Если Х, то Y; Если Y, то Z

Если Х, то Z

правило контрапозиции ПК:

 

Если X, то Y

Если не-Y, то не-X

 

сведение к «абсурду» СА:

 

Из Г и В выводимо противоречие (Х и не-Х)

Из Г выводимо не-В

 

доказывание от «противного» ДП:

Из Г и не-В выводимо противоречие (Х и не-Х)

Из Г выводимо В

Простой категорический силлогизм:

Фигуры, модусы и правила

 

1-я фигура	2-я фигура	3 фигура	4 фигура

 

Модусы первой фигуры:	Модусы второй фигуры:
1-й: Barbara (а, а, а) 2-й: Celarent (е,а,е) 3-й: Darii (a, i, i) 4-й: Ferio (е,i,o) 5-й: Barbari (a,а,i) 6-й: Celaront (е,а,o)	e,a,e; a,e,e; e,i,o; a,o,o; e,a,o; a,e,o
Модусы третьей фигуры:
a,a,i; i,a,i; a,i,i; e,a,o; o,a,o; e,i,o
Модусы четвертой фигуры:
a,a,i; a,e,e; i,a,i; e,a,o; e,i,o; a,e,o

ОБЩИЕ ПРАВИЛА ПРОСТОГО
КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА

1. Из двух отрицательных посылок нельзя получить правильного заключения (т.е. по крайней мере, одна из посылок должна быть утвердительной).

2. Если в выводе есть отрицательная посылка – заключение должно быть отрицательным.

3. Если обе посылки – положительные (утвердительные) суждения, заключение должно быть положительным.

4. Из двух частных посылок нельзя получить правильного заключения (т.е. одна из посылок должна быть общим суждением).

5. Если среди посылок есть частное суждение, заключение тоже должно быть частным.

6. Средний термин должен быть распределен хотя бы в одной из посылок.

7. Термин, который не распределен в посылке, не должен быть распределен в заключении.

 

 

Логические принципы индуктивных
умозаключений

 

1. Принцип редуктивного умозаключения РП:

Если X, то Y; Y

X

2. Принцип обобщающей индукции ОИ:

1. s¹ есть S; s¹ есть Р

2. s² есть S; s² есть Р

.

.

.

к. s^k есть S; s^k есть Р

к+1. Все S суть Р

3. Принцип умозаключения по аналогии ПА:

а есть Р¹; а есть Р²; …; а есть Рⁿ; но а есть также Q

в есть Р¹; в есть Р²; …; в есть Рⁿ

в есть Q

 

4. Принципы, используемые при

выявлении причинной зависимости

Принцип единственного сходства:

Случай 1. Когда имеют место факторы А,С,В, возникает явление Z.

Случай 2. Когда имеют место факторы А,К,М, возникает явление Z.

А является причиной Z

Принцип единственного различия:

Случай 1. Когда А, С, В, тогда Z.

Случай 2. Когда нет А, но есть С, В, тогда нет Z.

А является причиной Z.

 

Принцип сопутствующих изменений:

Случай 1. Когда А¹, С, В, тогда Z¹.

Случай 2. Когда А², С, В, тогда Z².

А является причиной Z.