
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заняття 8. Рух тіла під дією кількох сил. Рівновага тіл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сила – це рівнодіюча усіх сил, прикладених до тіла.
Замість здійснення геометричного додавання векторів можна знаходити суми проекцій цих векторів (сил) на обрані осі. Розглянемо, наприклад, рух тіла по похилій площині (рис.14).
Прискорення бруска за умовою спрямовано поралельно похилій площині.
Проекції сили на осі X і Y відповідно дорівнюють: F1x = mg· Sinα і F1y = – mg· Cosα. Оскільки проекція прискорення а на вісь Y дорівнює нулю, то сума проекцій усіх сил на цю вісь також дорівнює нулю. Тому: 0 = – mg· Cosα + F2. Звідси: F2 = mg· Cosα. Сила тиску бруска на похилу площину: N = F1y = – mg· Cosα. Сила тертя ковзання: F3 = μ ·|N| = μ · mg· Cosα Проекція рівнодіючої сили на вісь X: max = F1x – F3 = mg· Sinα – μ · mg· Cosα. Після скорочення на m отримаємо, що прискорення: ax = F1x – F3 = g · (Sinα – μ·Cosα). Якщо тіло рухається по похилій площині рівномірно (ax = 0), то тангенс кута α: tg α = μ.
Іноді важливо знати, за яких умов тіла, на які одночасно діють різні сили, не отримують прискорень і знаходяться у стані спокою. Такий стан часто називають станом рівноваги. Частина механіки, у якій вивчається рівновага тіл, називається статикою. Умовою рівноваги тіла, що не обертається, є те, щоб сума проекцій прикладених до тіла сил на будь-яку вісь дорівнювала нулю. Наприклад, сума проекцій на вісь X усіх прикладених до тіла сил:
F1x + F2x + F3x + … + Fnx = 0.
Обертаюча дія сили характеризується обертаючим моментом або моментом сили відносно осі обертання, який дорівнює добуткові абсолютного значення сили на відстань від осі обертання до лінії дії сили. Отже, момент сили F відносно осі, що проходить через точку О: М = F∙d. Величина d називається плечем сили. Моменти сил, що обертають тіло за годинниковою стрілкою, зазвичай беруть зі знаком “плюс”, а проти годинникової стрілки – “мінус”. Момент сили вимірюють у ньютоно-метрах (Н∙м). Умовою рівноваги тіла, що може обертатися навколо осі, є те, щоб алгебраїчна сума моментів прикладених до тіла сил відносно цієї осі дорівнювала нулю (правило моментів). Тобто: М1 + М2 + М3 +...+ Мn = 0, де М1,...., Мn – моменти сил F1, …, Fn відносно осі. При розв’язанні задач статики найчастіше користуються загальною умовою рівноваги тіла: Для того, щоб тіло знаходилося у рівновазі, необхідно, щоб дорівнювали нулю рівнодіючаприкладених до тіла сил і сума моментів цих сил відносно осі обертання.
Задача 28. З яким прискоренням а ковзає брусок по похилій площині з кутом нахилу 30°, якщо коефіцієнт тертя μ = 0,2?
Задача 30. Знайти сили, що діють на стрижні АВ і ВС (рис. 9), якщо α = 60°, а маса тягаря 3 кг. Задача 31. Знайти моменти сили тяжіння тягаря (рис. 16) відносно точок А, С і В, якщо довжина стрижня ВС дорівнює 1 м., α = 60°, а маса тягаря 4 кг.
Задача 32. Стрижень (рис. 17) масою 1 кг і довжиною 2 м лежить на опорах А і В. на відстані 0,5 м до стрижня прикладена сила 20 Н. Знайти реакції опор. Задача 33. З вершини похилої площини висотою 20 см і довжиною 1 м зісковзує брусок. Визначити швидкість бруска у кінці похилої площини, якщо коефіцієнт тертя μ = 0.
Д. З.: 1. §§ 30 – 32 і задачі, що залишилися нерозв’язаними на занятті. Лабораторна робота № 1. Визначення жорсткості пружини. Лабораторна робота № 2. Визначення коефіцієнта тертя ковзання.
Тема 1.3 Закони збереження.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.52 (0.011 с.) |

 В земних умовах на тіло окрім сил пружності та тяжіння завжди діє сила тертя. Для розв’язання механічних задач у цьому випадку необхідно пам’ятати, що у другому законі Ньютона:
В земних умовах на тіло окрім сил пружності та тяжіння завжди діє сила тертя. Для розв’язання механічних задач у цьому випадку необхідно пам’ятати, що у другому законі Ньютона:
 Отже, спочатку треба з’ясувати, які сили діють на тіло, їх абсолютні значення та напрями. Потім на рисунку зобразити ці сили, знайти їх рівнодіючу і, користуючись законами Ньютона, розв’язати задачу.
Отже, спочатку треба з’ясувати, які сили діють на тіло, їх абсолютні значення та напрями. Потім на рисунку зобразити ці сили, знайти їх рівнодіючу і, користуючись законами Ньютона, розв’язати задачу. Нехай по похилій площині з кутом α рухається брусок масою m. Знайдемо його прискорення.
Нехай по похилій площині з кутом α рухається брусок масою m. Знайдемо його прискорення.

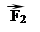
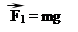 На рухомий брусок діють три сили: сила тяжіння; сила реакції опори (похилої площини), перпендикулярна до площини; сила тертя, спрямована вздовж похилої площини проти руху.
На рухомий брусок діють три сили: сила тяжіння; сила реакції опори (похилої площини), перпендикулярна до площини; сила тертя, спрямована вздовж похилої площини проти руху. За другим законом Ньютона:
За другим законом Ньютона: Спрямуємо осі координат X і Y вздовж похилої площини і перпендикулярно до неї.
Спрямуємо осі координат X і Y вздовж похилої площини і перпендикулярно до неї. Нехай тіло має закріплену вісь, що проходить через точку О (рис. 15), навколо якої воно може обертатися. Якщо на це тіло вздовж прямої АВ діє сила F, то воно може обертатися з прискоренням.
Нехай тіло має закріплену вісь, що проходить через точку О (рис. 15), навколо якої воно може обертатися. Якщо на це тіло вздовж прямої АВ діє сила F, то воно може обертатися з прискоренням.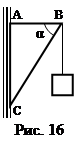 Задача 29. Яку силу треба прикласти до підйому вагонетки масою 600 кг по естакаді з кутом нахилу 20°, якщо коефіцієнт опору руху μ = 0,05?
Задача 29. Яку силу треба прикласти до підйому вагонетки масою 600 кг по естакаді з кутом нахилу 20°, якщо коефіцієнт опору руху μ = 0,05?



