Бұтақ тәрізді каталогы

Бұтақ тәрізді каталогы

 

 

Бұтақ тәрізді каталогы

1. C:\Student

2. C:\ Student

 

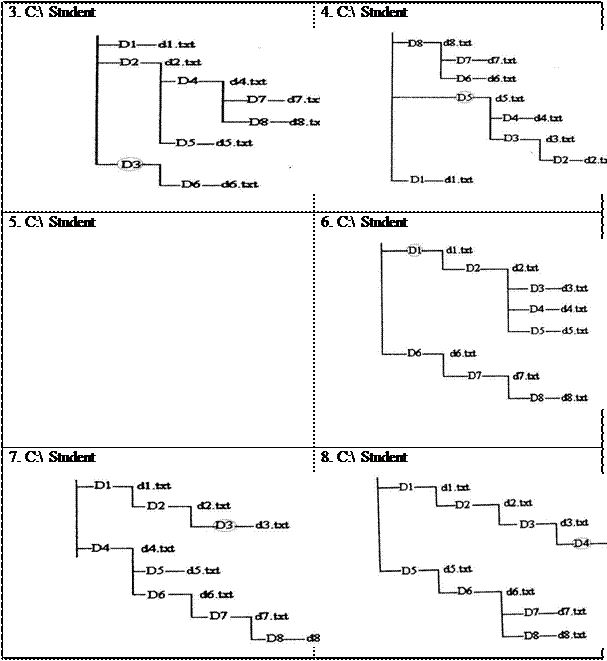
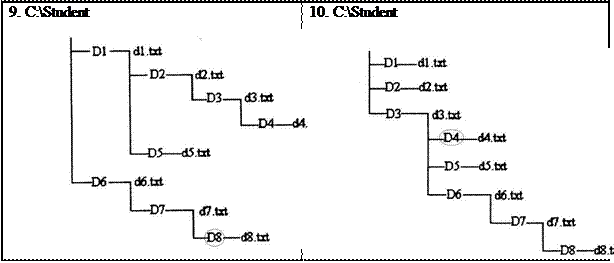
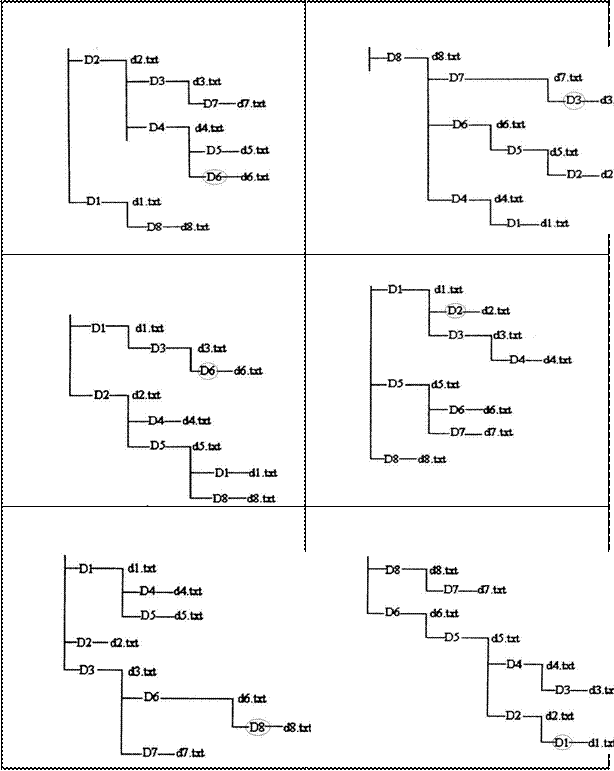11. C:\Student                                                12. C:\Student

 

13. C:\Student                                                14. C:\Student

 

15.C:\Student                                                 16. C:\Student

Тәжірибелік сабақ-10.Әр түрлі санау жүйесіндегі арифметикалық амалдар. Санау жҥйесі

Санау жүйесі – сандарды жазуға арналған ережелер мен арифметикалық операцияларды орындау мүмкіндігін беретін арнайы сандар жиыны. Санау жүйесі - санды атау және жазу әдістерінің жиынтығы. Санау жүйесі позициялық және позициялық емес болып, екіге бӛлінеді.

Позициялық емес жүйеде сандардың мәні (салмағы) оның тұрған орнына (позициясына) байланысты болмайды, мысал ретінде латын алфавитін пайдаланып жазылатын римсандарын айтуға болады: ССLХVII (100+100+50+10+7),қай жерде тұрса да С– жүз, L –елу, т.с.с.

Позициялық санау жүйесінде әр санның мәні оның тұрған орнына сәйкес, мысалы 777,7 санындағы алғашқы 7 саны – 7 жүздікті, екіншісі – 7 ондықты, үшіншісі

– 7 бірлікті, соңғысы – бірдің 7/10 бӛлігін кӛрсетеді.

Кез келген позициялық жҥйе ӛз негізі арқылы ерекшеленеді, олар екілік, сегіздік, ондық, он алтылық санау жҥйелері. Әр санау жҥйесінде негізі q сандардың жазылуын келесі ӛрнек арқылы кӛрсетуге болады:

аn-1

qn-1 + а

 

n-2

qn-2

+ ... + а1

q1 + а q0

+ а-1

q-1 + ... + а-

q-m

m

мұндағы ai

– санау жүйесіндегі сандар, п мен т санның бүтін және бӛлшек бӛліктері.

 

Мысалы, 125,4 санын

1×102 + 2 ×101 + 5×10

-1

+ 4 ×10

 

түрінде жазуға болады. Жалпы

полиномретінде келесі формуланы(1) пайдалану қажет:

n

m

Ap = an

pn + a

 

n-1

pn-1 + ... + a

p2 + a p1 + a

p0 + a-

p-1 + ... + a-

p-m ...

Ap  =  åak

k =-m

pk , (1)

мұндағы A – сан, p – санау жүйесінің негізі, n – жоғарғы разряд нӛмірі, m – тӛменгі разряд нӛмірі, k – ағымдағы разряд нӛмірі. ЭЕМ-мен жұмыс істеген кезде

 екілік, сегіздік, он алтылықсанау жҥйелеріқолданылатыны белгілі.

Кез келген ондық сан белгілі бір ереже арқылы екілік санға айналады және екілік санды қайтадан ондық санға айналдыру қиын емес. Ал әріптер мен символдарға келетін болсақ, олар ретті түрде жазылып, әрқайсысы тұрған нӛміріне сәйкес екілік кодқа ие болады. Екілік сандарды ондық сандар тәрізді қосуға, азайтуға, кӛбейтуге және бӛлуге болады.

Екілік сандарды ондық сандарға айналдыру ережесі қиын емес, ол үшін мына жолдарды қарастырайық:

Ондық сан: 0₁₀ 1₁₀ 2₁₀ 3₁₀ 4₁₀ 5₁₀ 6₁₀ ... 10₁₀ 11₁₀

Екілік сан: 0₂ 1₂10₂ 11₂ 100₂ 101₂ 110_{2 ...} 1010₂ 1011₂

Мұнда жоғарғы жолда 1-ден 11-ге дейінгі ондық сандар, ал тӛменгі жолда соларға сәйкес екілік сандар жазылған.

Сандарды ондық санау жҥйесіне аудару. Екілік сандарды ондық сандарға айналдыру олардың әрбір разрядын (1 немесе 0 санын) тұрған орнына байланысты екінің дәрежелеріне - 1, 2, 4, 8, 16, т.с.с. кӛбейтіп, шыққан сандарды қосу арқылы жүргізіледі.

Мысалы, 1011₂ болып жазылатын екілік сан ондық санға былай түрлендіріледі: 1011₂ = 1*2³+0*2²+1*2¹+1*2⁰ = 8 + 0 + 2 + 1 =11₁₀

 Сегіздік, он алтылық санау жүйелеріндегі сандарды ондықсанау жүйесіне аудару үшін – санның разрядтарын оның тұрған орнына байланысты дәрежелері арқылы кӛрсетілген негізіне кӛбейтіп, шыққан сандарға арифметикалық қосу амалын қолдану арқылы жүргізіледі:

C9,4₁₆ = 12^.16¹ + 9^.16⁰ + 4^.16^-1 = 201,25

 

Ондық жҥйедегі сандарды басқа жҥйеге аудару.Ол үшін – берілген ондық санның бүтін бӛлігін аударылатын жүйенің негізіне 0 қалдық қалғанша сатылап бӛліп, ал бӛлшек бӛлігін осы негізге кӛбейтіп, әрбір кӛбейтіндіден кейін оның бүтін бӛлігін айырып отыру керек – кӛрсетілген дәлдікке дейін. Мысалы: ондық сан - 125,625₁₀, екілік санғаайналдыру үшін осы санды екіге бӛлеміз, шыққан бӛліндіні тағы екіге бӛлеміз, одан шыққан санды да, осылайша бӛлінді бірге тең болғанша, біртіндеп екіге бӛле береміз. Ең соңғы бӛліндіден басталып жазылатын қалдық сандар тізбегі ізделініп отырған екілік санның таңбаларын құрайды, ал бӛлшекті екілік санау жүйесіне ауыстыру үшін бӛлшекті 2-ге кӛбейту керек. Кӛбейтіндінің бүтін бӛлігін екілік бӛлшектің үтірден кейінгі бірінші цифры ретінде алып, бӛлшек бӛлігін қайтадан 2-ге кӛбейту керек. Енді бұл кӛбейтіндінің бүтін бӛлігін екілік бӛлшектің келесі цифры ретінде алып, бӛлшек бӛлігін тағы 2-ге кӛбейту керек. т.с.с:

Мысалы: 125,625₁₀= 1111101, 101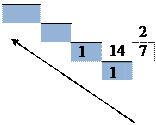₂

 

 

2

 

 

 

0,625 * 2=1,250 бүтін бӛлігі 1-ге тең; 0,250 * 2=0,500 бүтін бӛлігі 0-ге тең; 0,500 * 2=1,000 бүтін бӛлігі 1-ге тең;

 

Соңғы бӛлшектің бӛлшек бӛлігі 0-ге тең ауыстыру аяқталды. Ақырғы ондық бӛлшекті екілік жүйеге ауыстыру кезінде периодты бӛлшек алынуы мүмкін.

Мысалы:

0,3 * 2=0,6 бүтін бӛлігі 0-ге тең; 0,6 * 2=1,2 бүтін бӛлігі 1-ге тең; 0,2 * 2=0,4 бүтін бӛлігі 0-ге тең; 0,4 * 2=0,8 бүтін бӛлігі 0-ге тең; 0,8 * 2=1,6 бүтін бӛлігі 1-ге тең;

0,6 * 2=1,2 бүтін бӛлігі 1-ге тең; және т.с.с Жауабы: 0,310=0,0(1001)

1.1- кесте. Екілік сандарды сегіздік және он алтылық жүйеге аудару кестесі