
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Релятивистская теория атомного ядраСодержание книги
Поиск на нашем сайте
Важной характеристикой атомного ядра является его масса. Согласно теории относительности масса тела является переменной величиной, зависящей от скорости его движения:
где Кинетическую энергию частицы, ускоренной в постоянном электрическом поле, можно определить по формуле [62]
где e – заряд частицы; U- разность потенциалов. С учетом соотношения (200) последнее выражение примет вид
Величина Релятивистский закон сохранения энергии выражается формулой [61]
где Чтобы частица удерживалась ядром, сумма ее кинетической и потенциальной энергий должна быть отрицательной. Эта суммарная энергия называется энергией связи. Общая энергия ядра равна сумме энергий покоя протонов
Поделив все члены этого выражения на квадрат скорости света, получим
где Величина Рассмотрим с позиции теории относительности работу ускорителей и масс-спектрометров. Под действием электрического поля частица приобретает энергию
Магнитное поле действует на частицу с силой
где H – напряженность магнитного поля; r - радиус окружности, по которой движется частица. Решая совместно уравнения (204) и (205), находим
Из уравнения (205) находим
Путь, равный длине половины окружности, частица пройдет за время
Из уравнений (204) и (205) находим
где l – длина пути, на котором ускоряется частица. Согласно формуле (204) частица может достигнуть скорости света только в том случае, если длина пути l будет равна бесконечности. При этом согласно формулам (207) и (209) радиус окружности также должен быть равен бесконечности. Точные измерения масс атомов производятся на масс-спектрометрах с двойной фокусировкой. Ионы разной массы можно заставить поочередно двигаться по одной и той же траектории, изменяя ускоряющее напряжение при неизменном значении магнитного поля [42,106].Радиус круговой траектории найдем, решив систему уравнений (204), (205):
Это уравнение позволяет записать условие, при котором
Чтобы ион большей массы имел ту же траекторию, что и ион меньшей массы, нужно уменьшить разность потенциалов в Метод дублетов позволяет избежать трудностей, связанных с точными измерениями потенциалов. Движение ионов разных масс по одной и той же траектории обеспечивается одновременным изменением разности потенциалов и напряженности магнитного поля в
Чтобы вместо составляющей дублета малой массы сфокусировать другую составляющую, большей массы, нужно и разность потенциалов, и напряженность магнитного поля увеличить в С помощью формул (202) и (203) можно получить выражения для энергии связи ядра и релятивистской массы ядра: ΔEя =
где z - порядковый номер атома; A - массовое число. Таким образом, релятивистская масса любого ядра равна сумме масс покоя входящих в его состав протонов и нейтронов. Из выражения (214) находим V=C Для протона и нейтрона V = 0. Для ядер атомов углерода 6С12 и урана 92U238 скорость V соответственно равна 0,38261679×108 м×c-1 и 0,37985724×108 м×c-1 В масс-спектрометре Нира-Робертса ионы ускоряются разностью потенциалов U = 40 кВ [42]. По существующей ныне теории ионы приобретут кинетическую энергию Еk = eU. При измерении масс ионов методом дублетов ионы любого элемента будут иметь одну и ту же скорость, которую можно вычислить по формуле V = C При U = 40 кВ ион атома углерода 6С12 будем иметь скорость V = 0,008020107×108 м×c-1. Эта скорость в 47,7 раза меньше скорости, входящей в выражение (213). Здесь мы сталкиваемся с явным противоречием. Протоны и нейтроны, входящие в состав ядра, покоятся, но их массы меньше массы покоя протонов и нейтронов, находящихся в свободном состоянии. С другой стороны, массы ядерных протонов и нейтронов будут равны массам свободных покоящихся протонов и нейтронов только в том случае, если будут двигаться с весьма высокой скоростью. Получается, что релятивистская масса ядерных нуклонов равна массе покоя свободных нуклонов, не входящих в состав атомных ядер. Но ведь ядерные нуклоны, покинув ядро, также становятся свободными и ничем не должны отличаться от неядерных. Отсюда следует сделать вывод, что теория атомного ядра, созданная на основе теории относительности, неверна. С помощью масс-спектрометров измеряются массы покоя ионов. В справочных таблицах приводятся массы покоя атомов, которые получаются прибавлением к измеренным величинам масс ионов массы покоя электронов. Масса покоя атома mоа меньше его релятивистской массы, и поэтому moa < zmop + (A - z)mon + zmoe, где moe - масса покоя электрона. Такой результат получается потому, что мы анализируем эксперимент с позиции теории относительности, согласно которой масса является переменной величиной.
|
||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.01 с.) |

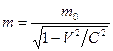 , (200)
, (200)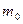 - масса покоя; V-скорость тела; C-скорость света.
- масса покоя; V-скорость тела; C-скорость света.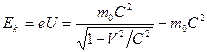 , (201)
, (201)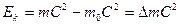 .
. называется полной энергией тела, а величина
называется полной энергией тела, а величина 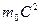 называется энергией покоя [61]. Кинетическая энергия увеличивает массу тела на величину
называется энергией покоя [61]. Кинетическая энергия увеличивает массу тела на величину 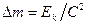 . Считается, что любая форма энергии, в том числе и потенциальная, изменяет массы тел [61,69].
. Считается, что любая форма энергии, в том числе и потенциальная, изменяет массы тел [61,69]. ,
,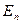 - потенциальная энергия, то есть энергия взаимодействия.
- потенциальная энергия, то есть энергия взаимодействия.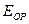 , нейтронов
, нейтронов 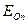 и энергии связи
и энергии связи  :
: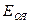 =
= 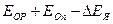 . (203)
. (203)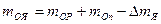 ,
,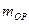 и
и 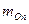 - суммы масс покоя протонов и нейтронов.
- суммы масс покоя протонов и нейтронов.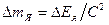 называется дефектом масс ядра. Таким образом, масса ядра меньше суммы масс составляющих его протонов и нейтронов [61].
называется дефектом масс ядра. Таким образом, масса ядра меньше суммы масс составляющих его протонов и нейтронов [61].
 . (204)
. (204)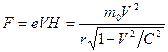 , (205)
, (205)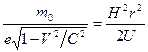 . (206)
. (206) . (207)
. (207)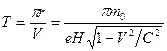 . (208)
. (208)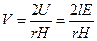 , (209)
, (209)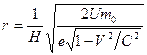 . (210)
. (210)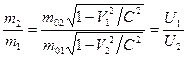 . (211)
. (211) раз. Тогда согласно формуле (209) скорость большого иона будет в
раз. Тогда согласно формуле (209) скорость большого иона будет в  одного иона, можно по формуле (211) определить массу
одного иона, можно по формуле (211) определить массу 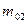 второго иона. При этом потребуются прецизионные измерения потенциалов
второго иона. При этом потребуются прецизионные измерения потенциалов 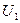 и
и  , что связано с большими трудностями [62]. Кроме того, на результатах измерений будет сказываться релятивистский эффект. При ускоряющей разности потенциалов 30-40кВ [42] релятивистский эффект будет ощущаться в шестой значащей цифре измеряемой величины.
, что связано с большими трудностями [62]. Кроме того, на результатах измерений будет сказываться релятивистский эффект. При ускоряющей разности потенциалов 30-40кВ [42] релятивистский эффект будет ощущаться в шестой значащей цифре измеряемой величины.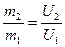 ;
;  . (212)
. (212) mояС2 ; (213)
mояС2 ; (213) = mоя +
= mоя +  = zmop + (A - z)mon, (214)
= zmop + (A - z)mon, (214)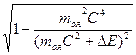 =C
=C 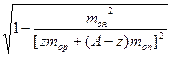 .
.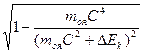 .
.


