
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовые явления в макрокосмосеСодержание книги
Поиск на нашем сайте
4.1. Повышение точности определения значений
Значение многих астрономических постоянных определены с недостаточной точностью. Выведенные нами формулы точно описывают как движение электронов в атомах, так и движение небесных тел. Они позволяют получить более точные значения некоторых констант. Геоцентрическая гравитационная постоянная определена с точностью до седьмой значащей цифры [28]:
До недавнего времени значение гравитационной постоянной было принято равным
Ввиду невысокой точности значения
В настоящее время получено более точное значение гравитационной постоянной [28]
С такой же точностью мы теперь можем записать значение массы Земли
Значение
где n=2,6616995×10-6 с-1 - средняя угловая скорость движения Луны; Согласно формуле (63) m= период обращения Луны вокруг Земли равен [59] Т = 27,32166127 суток. Принимая во внимание, что по ныне принятой теории значение l в b раз больше истинных, формулу (83) можно записать в виде m= В данной формуле l = 2 А. С учетом этого
Формулу (84) можно получить также из формулы (65). Значение m, определенное по формуле (82), в (1+a)3 раз больше значения m по формуле (83). Формула (82) дает значение m для изолированной системы Земля-Луна, то есть для того случая, когда Солнце и планеты солнечной системы не оказывали бы возмущающего действия на движение Земли и Луны. Формула (83) дает эффективное значение m. Под действием Луны Земля движется по орбите. Длина большой оси земной орбиты в МЗ/МЛ раз меньше лунной. Согласно формуле (83) для Луны mЛ = 488936×107 м3/с. Нетрудно убедиться, что
Исходя из приведенных значений mЗ, mЛ, МЗ и МЛ, находим эффективное значение гравитационной постоянной fЭ=6,65447×10-11Н×м2/кг2. Для сложных систем, подобных солнечной, вместо гравитационной постоянной f следует пользоваться эффективным зарядовым числом fЭ. Это число не является константой. Аналитически точно определить гравитационное число невозможно, так как его величина зависит от всех тел системы. На ХII съезде Международного астрономического союза в 1964 году утверждена новая система астрономических постоянных. Для астрономической единицы было принято округленное значение 149600000 км [23]. Методы радиолокационной астрономии позволили существенно повысить точность определения астрономической единицы. Наиболее вероятное ее значение 149598640 Из уравнений (61) можно получить новое выражение для m. Если орбита эллиптическая, то
Когда движущееся тело находится в апоцентре,
Так как (Vа×rа)/rn=Vn, то формула примет окончательный вид
Для круговой орбиты
Сравнивая формулы (85),(86) и (87), приходим к выводу, что движение тел по эллиптическим орбитам можно точно описать формулами, подобными формулам для круговых орбит. Так, для m можно записать
где
В таблице 4.1 периоды обращения планет вокруг Солнца выражены в секундах. Гелиоцентрические гравитационные числа для каждой планеты определялись по формуле (84), то есть с учетом того, что длины осей орбит в таблице 4.1 в b раз больше действительных. При определении средней скорости по формуле (89) длины больших осей орбит брались в b раз меньше справочных. В справочной литературе значение средних скоростей приводится с точностью до двух-трех значащих цифр. Формула (89) позволяет определить среднюю скорость с точностью до шестой значащей цифры.
Таблица 4.1 Элементы орбит планет
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.69.167 (0.006 с.) |


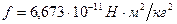 .
.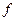 абсолютная масса Земли была принята равной [29]
абсолютная масса Земли была принята равной [29]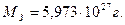
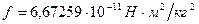 .
.
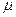 можно определить также по формуле [58,59]
можно определить также по формуле [58,59]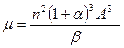 , (82)
, (82)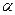 =0,00090768 - солнечное возмущение большой полуоси лунной орбиты; А=384400,2 км – расстояние от Земли до Луны;
=0,00090768 - солнечное возмущение большой полуоси лунной орбиты; А=384400,2 км – расстояние от Земли до Луны;  (83)
(83)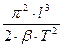 . (84)
. (84)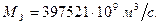
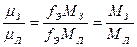 .
.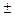 200 км [58]. Длины больших осей орбит планет принято выражать в астрономических единицах. Наиболее точные их значения приведены в [60]. Уточненные значения длин больших осей орбит планет в километрах приведены в таблице 4.1.
200 км [58]. Длины больших осей орбит планет принято выражать в астрономических единицах. Наиболее точные их значения приведены в [60]. Уточненные значения длин больших осей орбит планет в километрах приведены в таблице 4.1. . (85)
. (85)  .
.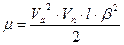 . (86)
. (86)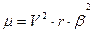 . (87)
. (87)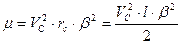 , (88)
, (88)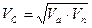 - средняя скорость; rc = l /2 – средний радиус. Из последней формулы получаем
- средняя скорость; rc = l /2 – средний радиус. Из последней формулы получаем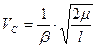 . (89)
. (89) , 106 км
, 106 км
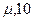 20 м3/с
20 м3/с



