
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектры водородо- и гелиеподобных атомовСодержание книги
Поиск на нашем сайте
При переходе электрона из стационарного состояния с большей энергией Е1 в стационарное состояние с меньшей энергией Е2 происходит излучение света с частотой [111]
Преобразуем эту формулу в формулу Бальмера
Величина
Постоянную Ридберга в формуле (139) можно также определить по формуле Ныне принятое значение
Эффект движения
Если бы большая ось эллиптической орбиты не изменяла своего положения в пространстве, то тогда формулы эффекта движения имели бы следующий вид:
Как видим, для всех орбит одного стационарного состояния эффект движения имеет одну и ту же величину. Вследствие вращения большой оси действительное значение эффекта движения для всех орбит будет разное. Во втором стационарном состоянии имеется одна эллиптическая орбита. Эффект движения для нее будет равен [71]
где V1 и V2 – скорости электрона соответственно в стационарных состояниях k1 и k2. В третьем стационарном состоянии имеются две эллиптические орбиты. Для орбиты с меньшим эксцентриситетом
Для второй эллиптической орбиты
В четвертом стационарном состоянии имеются три эллиптические орбиты. Для них соответственно можно записать
Эффект движения можно выразить также и через величины, непосредственно относящиеся к данной орбите:
Последняя формула является универсальной. Она справедлива для всех орбит любого атома. Согласно уравнению (139) энергия терма, выраженная в волновых числах, равна
В настоящее время энергию термов определяют по формуле Зоммерфельда. После разложения в ряд по степеням a2z2 для водородоподобных атомов она имеет вид [63,75]
где n - главное квантовое число; a - постоянная тонкой структуры спектров; j - внутреннее квантовое число. В таблице 5.6 приведены энергии термов, вычисленные по формулам (142) и (143) и взятые из справочника [73]. Уровни энергий обозначены символами, принятыми в рентгеновской спектроскопии. Расчетные величины, полученные по формулам (142) и (143), не совпадают со справочными данными. Формула (142) дает большее расхождение со справочными данными, чем формула (143).
Анализируя данные таблицы 5.7, приходим к выводу, что формулы (142) и (143) одинаково описывают тонкую структуру спектров. Разности энергий термов, вычисленных по этим формулам, совпадают. Как по формуле (142), так и по формуле (143) лэмбовский сдвиг уровней энергий не должен иметь место. Справочные данные включают в себя и разности энергий термов, обусловленных лэмбовским сдвигом. Уровни энергий до открытия спина электрона характеризовали двумя квантовыми числами: главным квантовым числом n и азимутальным квантовым числом nj [63]. Тонкую структуру спектров удалось объяснить с помощью трех квантовых чисел: главного квантового числа n, орбитального квантового числа l и внутреннего квантового числа Из таблицы 5.6 видно, что количество уровней энергии по новой методике расчета меньше, чем по существующей. Согласно формуле (143) часть уровней – вырожденные. Если не принимать во внимание вырожденные уровни энергии, то их количество, согласно формулам(142) и (143), совпадает. Формулу (143) можно записать в следующем виде [63]:
где nj = j+s = 1, 2, 3,…, n-1. Отсюда следует, что тонкую структуру можно описывать и по существующей теории с помощью двух квантовых чисел, не прибегая к понятию спина. Это подтверждает сформулированный в работе [76] вывод об отсутствии у электрона спина. Правила отбора накладывают ограничения на возможные переходы между энергетическими уровнями. Согласно этим правилам термы S комбинируют только с термами P, термы Р – только с термами S и Д, термы Д - только с термами Р и F и т.д. [27]. Переходы возможны при условии, что
На рис.5.4 приведены схемы уровней энергии в атоме водорода согласно новой и существующим методикам расчета. По новой методике из второго стационарного состояния в первое возможны два перехода, из третьего в первое – три, из третьего во второе – шесть. По существующей методике из второго стационарного состояния в первое возможны два перехода, из третьего в первое – два, из третьего во второе – семь. Если не применять правила отбора, то тогда получим три перехода из второго стационарного состояния в первое, пять переходов – из третьего в первое и пятнадцать переходов – из третьего во второе. Таблица 5.6 Спектральные термы водородоподобных атомов
Продолжение табл. 5.6
Ион лития Li ++
Таблица 5.7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.119.68 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

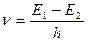 .
.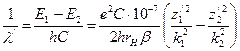 .
.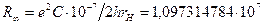 м-1 – постоянная Ридберга, имеющая одно и то же значение у всех атомов. С учетом этого формула Бальмера примет вид
м-1 – постоянная Ридберга, имеющая одно и то же значение у всех атомов. С учетом этого формула Бальмера примет вид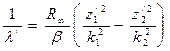 . (139)
. (139)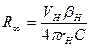 . (140)
. (140)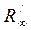 для атома водорода определяется по формуле (101). Сравнив формулы (101) и (140), видим:
для атома водорода определяется по формуле (101). Сравнив формулы (101) и (140), видим: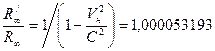 .
. удобно вычислить по формулам, в которых скорость электронов выражена через его скорость на боровской орбите. При движении по круговой орбите
удобно вычислить по формулам, в которых скорость электронов выражена через его скорость на боровской орбите. При движении по круговой орбите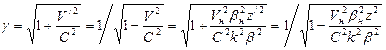 . (141)
. (141)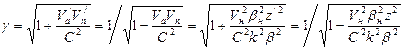 .
.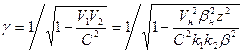 ,
,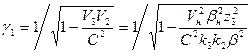 .
.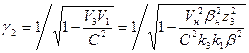 .
. ;
; 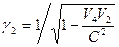 ;
; 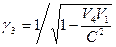 .
.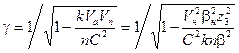 .
.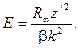 (142)
(142)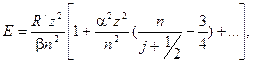 (143)
(143)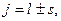 где s - спин электрона. Наличие спина у электрона должно привести к появлению новых линий в спектрах. В действительности количество линий в спектрах значительно меньше, чем предсказывает теория. Чтобы устранить это противоречие, пришлось ввести правила отбора.
где s - спин электрона. Наличие спина у электрона должно привести к появлению новых линий в спектрах. В действительности количество линий в спектрах значительно меньше, чем предсказывает теория. Чтобы устранить это противоречие, пришлось ввести правила отбора.
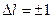 и
и 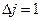 или 0. Эти правила не очень строгие. Так, в [75] и [69] отмечается, что при их выполнении осуществляются наиболее интенсивные переходы. Менее интенсивные переходы возможны и в том случае, если
или 0. Эти правила не очень строгие. Так, в [75] и [69] отмечается, что при их выполнении осуществляются наиболее интенсивные переходы. Менее интенсивные переходы возможны и в том случае, если 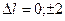 и
и 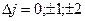 [75].
[75].


