
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Орбитальное движение тела малой массыСодержание книги
Поиск на нашем сайте
Два взаимодействующих тела заставляют друг друга двигаться по орбитам. Если масса центрального тела очень велика и его движением можно пренебречь, то тогда для единичной массы малого тела можно записать законы сохранения энергии и момента количества движения в следующем виде [51]:
где V – орбитальная скорость; r – радиус – вектор; Vt – тангенциальная скорость. При гравитационном взаимодействии Для тела, движущегося по эллиптической орбите, будут выполняться следующие равенства:
где Решая данную систему уравнений, находим
где Теперь для каждой возможной орбиты интеграл энергии и орбитальную скорость можно выразить следующими формулами: для эллиптической
для круговой
для параболической
для гиперболической
Для каждого типа орбит тангенциальная скорость будет равна
Найдя значения для эллиптической орбиты для круговой
для параболической для гиперболической
Радиальную скорость определим по формуле
Для эллиптической орбиты
для круговой
для параболической
для гиперболической
Уравнения орбит можно получить из соотношения
для эллиптической
для круговой
для параболической
для гиперболической
где Время прохождения телом элемента длины орбиты
Из этого выражения находим: для эллиптической орбиты
для параболической
для гиперболической
Выведем теперь второй закон Кеплера. Секториальная скорость
Подставляя в это уравнение значение
Таким образом, для всех типов орбит секториальная скорость является постоянной величиной. Площадь, описываемая радиусом-вектором за время
Выражение для третьего закона Кеплера получим, найдя величину полупериода по формуле (57) для эллиптической орбиты:
При наблюдении с Земли за искусственными спутниками удобнее пользоваться формулами, выражающими время через истинную аномалию: для эллиптической орбиты
для параболической
для гиперболической
В любой момент можно определить не только координаты тела, но и направление его движения. Пользуясь зависимостью для эллиптической орбиты
для параболической
для гиперболической
где Можно сказать, что парабола является эллипсом с бесконечно большой осью. Скорость тела, движущегося по параболической траектории, в бесконечности стремится к нулю. Скорость же тела, движущегося по гиперболической траектории, в бесконечности будет стремиться к вполне определённой конечной величине. Её можно определить исходя из закона сохранения энергии:
откуда
|
||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.159 с.) |

 ;
;  ,
, , где
, где 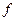 - гравитационная постоянная;
- гравитационная постоянная;  - масса центрального тела.
- масса центрального тела.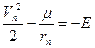 ;
;  ;
;  ,
, и
и  - скорости тела в перицентре и апоцентре;
- скорости тела в перицентре и апоцентре; 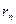 и
и 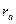 - перицентральный и апоцентральный радиусы.
- перицентральный и апоцентральный радиусы.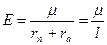 ,
, - длина большой оси эллипса.
- длина большой оси эллипса.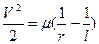 ;
;  ;
; ;
; 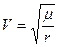 ;
; ;
; 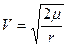 ; (53)
; (53)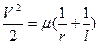 ;
;  .
. .
.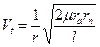 ;
;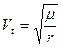 ;
; ;
;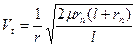 .
.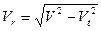 .
. ;
;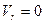 ;
;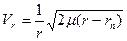 ;
; .
.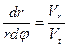 ; (54)
; (54)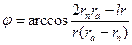 или
или 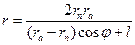 ;
;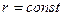 ;
;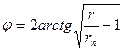 или
или 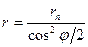 ; (55)
; (55)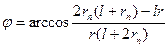 или
или 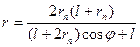 ,
, - истинная аномалия. Уравнения (55) выражают первый закон Кеплера.
- истинная аномалия. Уравнения (55) выражают первый закон Кеплера.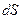 равно
равно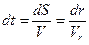 . (56)
. (56) ;
;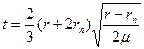 ; (57)
; (57) .
.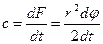 .
.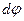 из (54), а значение
из (54), а значение 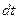 из (56), получим
из (56), получим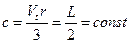 .
. , равна
, равна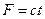 .
.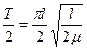 или
или 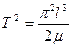 .
.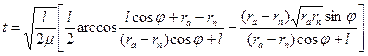 ;
;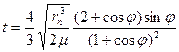 ;
;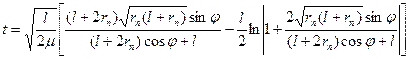 .
.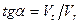 , находим:
, находим: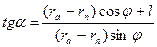 ;
;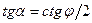 ;
; ,
,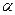 - угол между радиусом – вектором и направлением движения.
- угол между радиусом – вектором и направлением движения.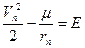 ;
; 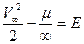 ,
, .
.


