
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий закон отражения и преломления волнСодержание книги
Поиск на нашем сайте
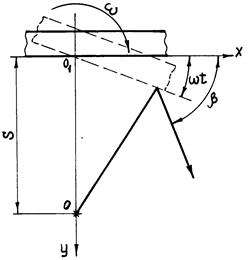
При отражении волн от зеркала, находящегося в сложном движении (рис. 1.6), уравнение семейства вторичных волн запишется в следующем виде:
где x0, y0 и t0 – соответственно координаты и время встречи каждого луча с зеркалом; x и y – координаты точек вторичных волн в рассматриваемый момент времени; t – промежуток времени с момента излучения волн до момента образования данного семейства.
Рис. 1.6. Отражение волны от произвольно движущегося зеркала Параметрические уравнения огибающей данного семейства
где Направление отраженного луча определяется направлением нормали к фронту отраженной волны:
Можно показать, что все вышевыведенные законы отражения и преломления волн являются частным случаем общего закона. Для этого нужно в каждом конкретном случае найти значения x0, y0, t0 и их производные и подставить в формулы (4)-(8). Эти формулы позволяют решать и другие задачи. Например, если зеркало движется с переменной скоростью по закону V=V0+at0, где V0 - скорость движения зеркала в момент излучения волны; а – ускорение, то тогда
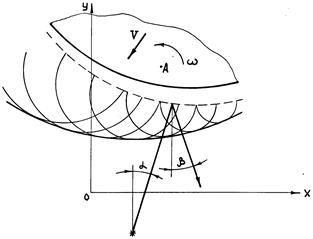
Подставив производные x0 ,y0 и t0 в уравнения (4)-(8), получим искомые зависимости. Конечный результат ввиду громоздкости не приводим. Если зеркало вращается, то координаты точек встречи каждого луча точечного источника с зеркалом (рис. 1.7) выразятся формулами
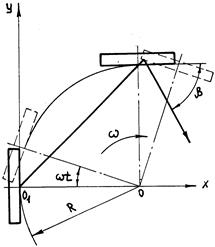
В опыте Саньяка зеркала вращаются по окружности радиуса R (рис. 1.8).
Рис. 1.7. Отражение сферической волны
Значение координат x0 и y0 можно вычислить по формулам
Общий закон отражения и преломления волн справедлив как в оптике, так и в акустике [12].
Рис. 1.8. Ход лучей в опыте Саньяка
1.6. Релятивистский закон отражения волн
Закон отражения световых волн от движущегося плоского зеркала выводится следующим образом. Пусть зеркало движется относительно наблюдателя и источника света вдоль своей нормали (рис.1.9). В системе отсчета S, в которой зеркало покоится, справедлив обычный закон отражения, то есть угол падения α равен углу отражения β. В системе отсчета S/, в которой находится наблюдатель, это равенство нарушается. Угол падения α/ не равен углу отражения β/. Соотношения между углами α и α/ и соответственно между углами β и β/ имеют следующий вид [13]:
Рис. 1.9. Отражение света от движущегося зеркала
Приравнивая правые части уравнений, закон отражения световых волн от движущихся зеркал в системе отсчета S/ можно записать в следующем виде:
Эти уравнения легко преобразуются к виду
Сравнивая формулы (15)-(17) с формулами (1)-(3), обнаруживаем их поразительное сходство. Зависимость между углом падения и углом отражения в системе отсчета, в которой находятся наблюдатель и источник света, такая же, как и в системе координат, связанной с неувлекаемым эфиром, согласно классической физике. В первом случае зеркало движется со скоростью V относительно наблюдателя, а во втором – относительно неувлекаемого эфира. Если связать систему координат с движущимся относительно эфира зеркалом, то будем наблюдать следующую картину (рис.1.10). В момент излучения волны зеркало находится на расстоянии S от источника света. Луч, падающий на зеркало под углом α, встретится с ним в точке m через промежуток времени
В системе координат, связанной с зеркалом, луч падает на зеркало под углом α1. Из треугольника dem и de1m находим
Рис. 1.10. Ход лучей в системе координат, связанной с зеркалом
Отразившийся луч света пройдет отрезок mn за промежуток времени
Из треугольника kmn и km1n для отраженного луча находим
Подставляя в последнюю формулу значения sinβ и cosβ, согласно формулам (1) и (2) получим
Сравнив это с формулой (18), видим
Итак, согласно теории о неувлекаемом эфире, в системе координат, связанной с движущимся зеркалом, для падающей и отраженной волн имеет место равенство углов падения α1 и углов отражения β1. Эти углы образованы нормалью к зеркалу km1 и отрезками e2m1 и m1n. Они указывают на кажущиеся направления распространения падающей и отраженной волн относительно зеркала. Отрезки em и mn, изображенные сплошными линиями, являются нормалями к фронтам падающей и отраженной волн. Они указывают на истинное направление распространения волн относительно эфира. Зависимость между углами α и β, образуемыми этими отрезками с нормалью к зеркалу km, выразится формулами (1)-(3). При выводе релятивистского закона отражения волн от движущихся зеркал было принято без доказательства, что в системе отсчета, связанной с движущимся зеркалом, углы падения и отражения волн равны. Значения углов падения и отражения волн в системе координат, связанной с зеркалом, можно выразить через значения соответствующих углов в системе координат, связанной с эфиром, следующими формулами:
(19)
(20)
Приравняв правые части уравнений, получим новые выражения закона отражения волн от поступательно движущихся зеркал в системе координат, связанной с эфиром:
Эти уравнения можно легко преобразовать в формулы (1), (2) и (3). Сравнивая уравнения (22), (23) и (24) с уравнениями (12), (13) и (14), замечаем, что уравнение (14) имеет такой же вид, как и уравнение (24). Уравнения (12) и (13) преобразуем к виду
Множители левых и правых частей уравнения равны
В этом легко убедиться, если принять во внимание уравнение (14). После сокращения на общий множитель уравнения (25) и (26) становятся подобными уравнениям (22) и (23). Теперь релятивистский закон отражения волн от движущихся зеркал можно записать в следующем виде:
Как видим, законы отражения от поступательно движущихся зеркал, согласно теории относительности и согласно теории неувлекаемого эфира, выражаются подобными уравнениями. Однако согласно теории относительности процессы отражения волн рассматриваются в системах отсчета, связанных либо с наблюдателем, либо с движущимся зеркалом, а согласно теории неувлекаемого эфира эти процессы рассматриваются в системах координат, связанных либо с эфиром, либо с зеркалом. Как изменятся величины углов падения и углов отражения при переходе от одной системы отсчета к другой в первом случае, и как они будут меняться при переходе от одной системы координат к другой во втором случае, можно вычислить соответственно по формулам (9)-(11) и (19)-(21). Формулы, полученные с помощью теории относительности, и формулы, полученные с помощью теории неувлекаемого эфира, имеют разный вид. Для их сравнения преобразуем формулы (9)-(11) к виду
Сравнив полученные выражения с формулами (19)-(21), замечаем, что абсолютные величины углов, согласно теории относительности и теории эфира, не равны. Это является следствием ошибочных допущений в теории относительности.
1.7. Закономерности распространения волн
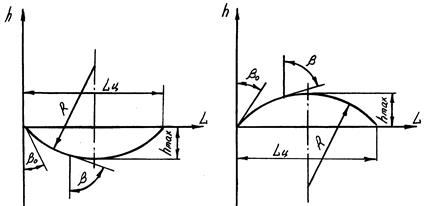
Выше были даны выводы формул для волн, распространяющихся в однородных средах. Однако во многих областях науки и техники приходится иметь дело с волнами, распространяющимися в неоднородных средах. В качестве примеров рассмотрим распространение акустических волн в океане и световых волн в воздушной оболочке Земли. Скорость звука в океане растет с увеличением глубины траектории луча, а скорость света растет с увеличением высоты траектории луча. Если пренебречь кривизной поверхности земного шара, то траектория акустического луча в океане и траектория светового луча в воздушной оболочке Земли изобразятся кривыми, показанными соответственно на рис. 1.11,а и 1.11,б. При распространении волн в плосконеоднородных средах выполняется следующая зависимость:
где β0 и β – углы между осью h и направлением луча соответственно в точке входа его в среду и в любой произвольной точке траектории; С и С0 – скорости распространения волн в этих точках.
а) б) Рис. 1.11. Распространение волн в плосконеоднородных средах:
Скорость звука в океане и скорость света в атмосфере Земли можно выразить формулой [6,14]
С учетом этого из соотношения
находим координату L
Это уравнение можно преобразовать к виду
Таким образом, убеждаемся, что траекториями лучей являются окружности с радиусами R=C0/ksinβ0 и координатами их центров L=(C0ctg β0)/k; h= Время пробега волной элемента длины траектории луча dS равно
Полное время пробега, выраженное через угол β, равно
Далее находим длину цикла Lц, максимальную глубину (высоту) траектории hmax и время цикла tц [15]:
При распространении волн в сферически-неоднородных средах (рис. 1.12) выполняется зависимость [16]
где β0 и β – углы преломления; С0 и
а) б) Рис. 1.12. Распространение волн в сферически-неоднородных
Из последнего выражения следует
С учетом этого из соотношения
находим величину центрального угла
Центральный угол полного цикла
а длина цикла Глубину траектории луча в каждый данный момент можно определить из выражения
откуда максимальная глубина траектории
Время пробега волной элемента длины траектории луча dS равно
Полное время пробега, выраженное через угол β, равно
Время цикла
Фаза гармонической волны в любой точке траектории α=2πft, где f – частота сигнала. В таблице 1.1 приведены результаты расчета траекторий акустических лучей в океане. Буквами без штрихов и со штрихами обозначены величины, полученные соответственно с учетом и без учета кривизны океана.
Таблица 1.1
|
||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

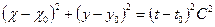 ,
,
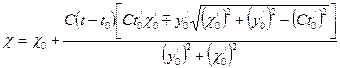 ; (4)
; (4) 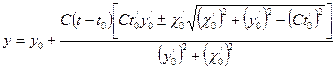 , (5)
, (5)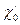 ,
, 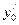 и
и 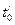 - производные от x0, y0 и t0.
- производные от x0, y0 и t0.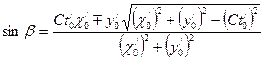 ; (6)
; (6)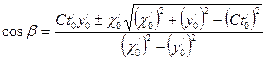 ; (7)
; (7)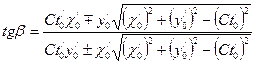 . (8)
. (8)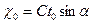 ;
; 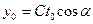 ;
;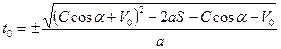 .
.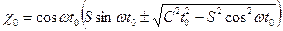 ;
;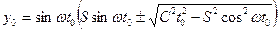 .
.
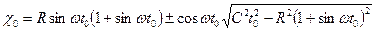 ;
; 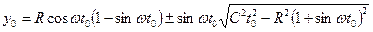 .
.
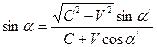 ;
; 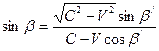 ; (9)
; (9)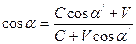 ;
; 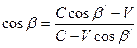 ; (10)
; (10)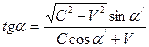 ;
; 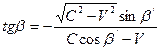 . (11)
. (11)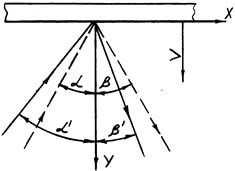
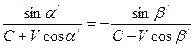 ; (12)
; (12) 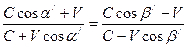 ; (13)
; (13)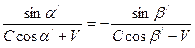 . (14)
. (14)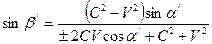 ; (15)
; (15)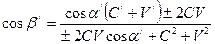 ; (16)
; (16)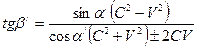 . (17)
. (17)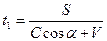 .
.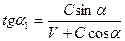 . (18)
. (18)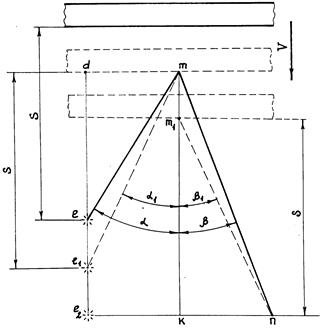
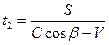 .
.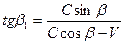 .
.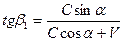 .
.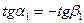 .
.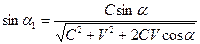 ,
,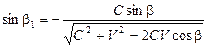 ;
;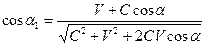 ,
,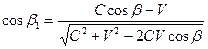 ;
;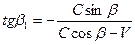 . (21)
. (21)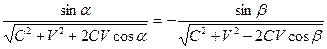 , (22)
, (22)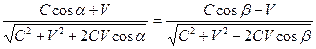 , (23)
, (23)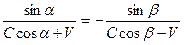 . (24)
. (24)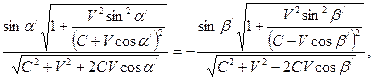 (25)
(25)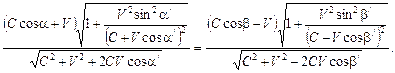 (26)
(26)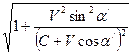 =
= 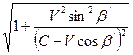 .
.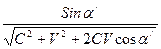 = –
= – 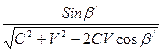 ,
,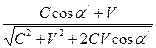 =
= 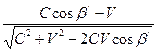 ,
,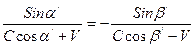 .
.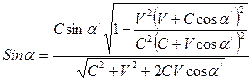 ;
;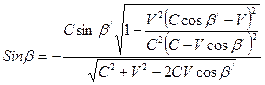 ;
;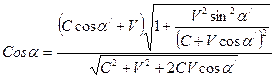 ;
;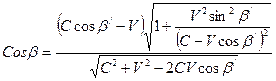 ;
;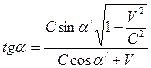 ;
; 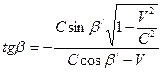 .
.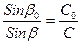 ,
,
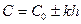 , где h – глубина (высота) траектории луча; k – градиент скорости распространения волны. Теперь последнее выражение можно записать следующим образом:
, где h – глубина (высота) траектории луча; k – градиент скорости распространения волны. Теперь последнее выражение можно записать следующим образом: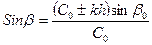 .
.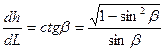
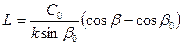 .
.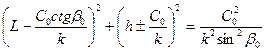 .
.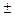 C0/k. Положительное значение координаты h относится к световым лучам, а отрицательные – к акустическим.
C0/k. Положительное значение координаты h относится к световым лучам, а отрицательные – к акустическим.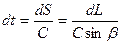 .
.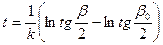 .
.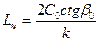 ;
; 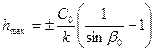 ;
; 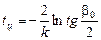 .
.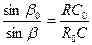 ,
,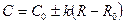 - скорости распространения волн на расстояниях R0 и R от центра Земли.
- скорости распространения волн на расстояниях R0 и R от центра Земли.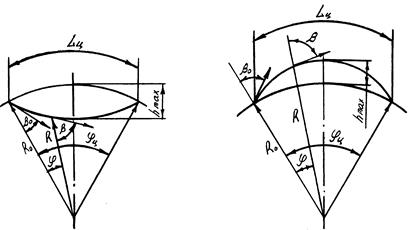
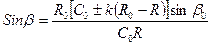 .
.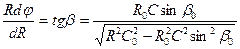
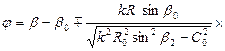
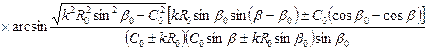 .
.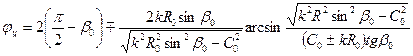 ,
,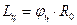 .
.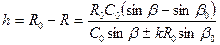 ,
,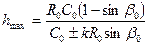 .
.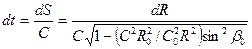 .
.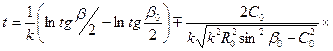
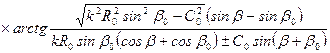 .
.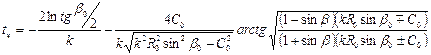 .
.


