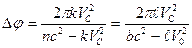Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие закономерности в космических и атомных системахСодержание книги
Поиск на нашем сайте
P = kh = kmV1r1b1, где h – постоянная Планка; k – целое число; m – масса электрона; V1 – скорость электрона; r1 – радиус боровской орбиты; L = kV1r1 Планеты и спутники планет движутся по стандартным орбитам. Момент количества движения единичной массы планет квантуется в соответствии с формулой (90). В таблице 4.2 приведены результаты расчетов элементов орбит планет по новой методике. Расчет проводился в такой последовательности. Вначале по данным таблицы 4.1 нашли значение q для первого стационарного состояния q = 929,481·106 км2·с-1, затем из соотношений T= находим r= Значения T взяли из таблицы 4.1, полагая, что они определены экспериментаторами точно. Все другие величины у большинства планет получены расчетом. Таблица 4.2 Элементы орбит планет согласно новой методике расчета
Сравнивая данные таблиц 4.1 и 4.2, можно сделать следующие выводы. При расчете по существующей методике принято, что гравитационное число у всех планет имеет одну и ту же величину. Согласно же новой методике каждая планета имеет свое гравитационное число. Момент количества движения единичной массы планет квантуется. По существующей методике у первых шести планет m=1,32714·1020 м3/с. Но планеты только в том случае имели бы одинаковые значения m, если бы не оказывали возмущающего действия друг на друга. При этом величина этой постоянной была бы равна m = fMC = 6,67259×10-11×1989,00530 = 1,32718×1020 м3/с2.
Таким образом, у первых шести планет m таково, как если бы другие планеты не существовали. У дальних трех планет значение m существенно отличается от значения m для первых шести планет. В справочной литературе с высокой точностью приводятся периоды обращения планет и длины больших осей их орбит. Периоды обращения точно определяют экспериментально, а длины осей вычисляют, считая, что третий закон Кеплера абсолютно точен. Третий закон Кеплера записывается в виде
где T2 и T1 – периоды обращения двух каких-либо планет; На самом деле третий закон Кеплера неточен. Согласно формуле (83) T2= Отношение квадратов периодов обращения двух планет будет равно
Значения Теперь рассчитаем по новой методике элементы орбит спутников планет. У Земли один спутник – Луна. Расстояние от Земли до Луны А=384400,2 км. Длина большой оси орбиты Луны Закон квантования момента количества движения (90) может выполняться только при условии, если скорость тела и радиус его орбиты будут равны соответственно V = где V0 и r0 – скорость и радиус орбиты тела, находящегося в первом стационарном состоянии. Выразив через V0 и r0 период обращения тела, получим T Отношение периодов обращения двух тел в планетарной системе будет равно
Таблица 4.3 Элементы орбит спутников планет
Так как периоды обращения планет или спутников определены очень точно, то с помощью этого уравнения легко определяются номера их стационарных состояний. Далее находим моменты количества движения единичной массы тел по формуле L= Значения В атомах электроны движутся с очень высокими скоростями и поэтому при расчетах всегда нужно учитывать эффект движения. В планетарных системах космоса планеты и спутники движутся медленно. Эффект движения можно не учитывать. Он становится заметным только за периоды, исчисляемые столетиями. Рассмотрим это на примере Меркурия. Согласно формуле (81) перигелий планеты повернется на угол
за один оборот вокруг Солнца. После подстановки известных величин и перевода радианов в секунды получаем Dj=13,99// за столетие. По расчетам, приведенным в [61], Dj=42,56//, то есть в три раза больше. Наблюдаемый же угол поворота перигелия Меркурия за столетие Dj=5599,74//. На скорость вращения перигелия Меркурия влияет очень много факторов. Точный учет их является сложнейшей задачей. В связи с этим достоверность цифры 42,56// сомнительна. Произведенные расчеты показали, что движение небесных тел и движение электронов в атомах происходит по одним и тем же законам. Квантовые явления наблюдаются не только в атомах, но и в космических планетарных системах.
ГЛАВА 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.202 (0.01 с.) |



 I+m/mя, mя – масса ядра. Так как масса у всех электронов одинакова, то, следовательно, квантуется и момент количества движения единичной массы
I+m/mя, mя – масса ядра. Так как масса у всех электронов одинакова, то, следовательно, квантуется и момент количества движения единичной массы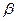 1 = k q. (90)
1 = k q. (90) и rVb=kq (91)
и rVb=kq (91)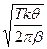 ; V=
; V= 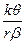 . (92)
. (92) , 106 км
, 106 км 
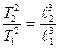 , (93)
, (93)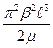 . (94)
. (94)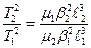 . (95)
. (95)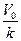 ; r = r0k2,
; r = r0k2, .
.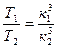 .
.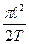 .
.