Свободные и вынужденные колебания.

 

Частота колебаний математического маятника (или их период) зависит от длины нити, на которой подвешен груз, и от ускорения свободного падения в том месте, где находится маятник. Она не зависит от массы груза и от амплитуды колебаний. В этом легко убедиться, проделав простой опыт. Если подвесить на нити груз определённой массы, измерить частоту качаний такого маятника, а затем удлинять или укорачивать нить, частота колебаний будет меняться пропорционально квадратному корню из длины нити. При этом масса подвешенного груза не имеет никакого значения. Вы можете подвесить на нити самые различные предметы и убедиться в том, что при одной и той же длине нити частота, с которой качаются все подвешенные предметы, будет одинаковой. Точно так же легко убедиться в том, что частота и амплитуда колебаний никак не связаны между собой. Амплитуда зависит от того, насколько вы при запуске колебания отклонили груз от состояния равновесия. Если вы отведёте его на большое расстояние, размах качаний будет большим, но их частота будет такой же, как если бы вы только слегка сдвинули его. Также поскольку в нашем опыте мы не можем избавиться от сопротивления воздуха, колебания маятника будут постепенно затухать, и амплитуда будет уменьшаться вплоть до полной остановки маятника. Однако всё это время частота колебаний будет оставаться постоянной. Период колебания любого математического маятника можно вычислить по формуле:

Т = 2π√¯l / g,

где l – длина нити, а g – ускорение свободного падения.

Если у вас есть маятниковые часы типа ходиков, вы можете отрегулировать их ход, передвигая груз на маятнике. Чем ниже он опустится, тем медленнее будут идти часы. Это замедление будет пропорционально квадратному корню из длины маятника. Если увеличить расстояние от груза до точки подвески в четыре раза, то минутная стрелка, совершавшая полный оборот за час, теперь будет проделывать это за два часа. По формуле маятника можно точно вычислить ускорение свободного падения в любой точке Земли, а также на Луне или каком– либо другом небесном теле. Всё, что для этого требуется, это измерить длину нити и период колебаний любого подвешенного к ней груза. Для того чтобы точность определения периода была достаточно большой, надо подсчитать число колебаний (N) за достаточно продолжительное время (t), а затем вычислить период, разделив t на N.

До сих пор мы говорили о тех колебаниях, которые будет совершать тело, если его вывести из состояния равновесия и затем предоставить самому себе. Такие свободные   колебания будут происходить с частотой, которую называют собственной. Но колебание может быть вызвано и другими причинами, например периодически меняющейся внешней силой. Звонарь может раскачивать язык колокола с той частотой, которая соответствует требуемой мелодии. Игла в швейной машине двигается вверх и вниз под влиянием действующей на неё силы тяги от мотора. В этом случае система совершает вынужденные колебания.  

 

Резонанс

 

А что произойдёт, если периодическая сила действует на систему, способную совершать собственные колебания? Рассмотрим это на примере качелей (рис. 58). Для того чтобы раскачать качели, их отводят на некоторое расстояние от точки равновесия и отпускают. Качели за время, равное периоду, совершают одно колебание, возвращаются в исходную точку, и в этот момент, когда их скорость становится равной нулю, их толкают в том направлении, в котором они бы всё равно начали двигаться. То, что толчок делается в тот момент, когда качели возвращаются в первоначальное положение, означает, что прилагаемая сила будет направлена на преодоление сил сопротивления для того, чтобы колебания были незатухающими. При совпадении частоты вынуждающей силы с собственной частотой колебательной системы (качелей) будет наблюдаться резкое возрастание амплитуды.

 

Рис. 58. При раскачивании качелей частота периодической внешней силы совпадает с частотой собственных колебаний качелей

 

Возрастание амплитуды вынужденных колебаний при совпадении частоты вынуждающей силы с собственной частотой колебательной системы называют резонансом.  

Резонанс играет очень большую роль в самых разнообразных природных и технических процессах, причём эта роль может быть как положительной, так и отрицательной. Наиболее известный случай, связанный с разрушительным действием резонанса, произошёл в 1905 г. в Петербурге (рис. 59). Кавалерийский эскадрон чётким церемониальным шагом переходил через реку Фонтанку по Египетскому мосту. Частота ударов лошадиных копыт совпала с собственной частотой колебаний моста, и тот обрушился. Поэтому теперь при движении по мостам войскам приказывают идти вольным шагом, а поезда снижают скорость или, наоборот, проносятся через мост с максимальной скоростью, для того чтобы период колебаний от ударов колёс о стыки рельсов был заведомо больше или меньше собственных колебаний моста.

Библейский рассказ о том, как рухнули стены города Иерихон, когда осаждавшие разом громко затрубили во все трубы, может иметь под собой вполне реальную основу. Такое могло произойти, если достаточно мощные звуковые колебания звучащих в унисон труб совпали с частотой собственных колебаний стен города.

Как будет рассказано дальше, многие природные явления представляют собой колебательные процессы: это и звук, и свет, и передача сигналов в телевизорах и мобильных телефонах, и радиоактивное излучение. Частота колебаний в этих процессах может в большей или меньшей степени совпадать с частотой колебаний других систем, окружающих их и влияющих на них.

 

Рис. 59. Египетский мост в Санкт-Петербурге

 

Явление резонанса используется при конструировании различных приспособлений, применяемых в средствах связи, медицине и во многих других областях. Для того чтобы усилить или ослабить какие-либо колебания, надо повлиять на частоту колебаний тех объектов, которые действуют на интересующее нас явление или процесс. Чем ближе будут частота собственных колебаний и частота внешней силы, тем больше будет амплитуда возникающих вынужденных колебаний. В дальнейшем мы рассмотрим конкретные примеры резонансных процессов.

 

Проверьте свои знания

 

1. Какие факторы определяют частоту колебаний математического маятника?

2. Что такое свободные и вынужденные колебания?

3. В каких случаях возникает явление резонанса?

 

Задания

 

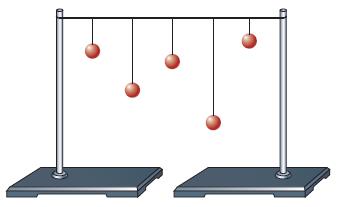
1. Изучите особенности колебания математического маятника. Для этого подвесьте грузик на тонкую нить, отведите его от состояния равновесия и отпустите. Пронаблюдайте, как будет изменяться амплитуда колебаний маятника, и объясните, почему она будет постепенно уменьшаться. Будет ли при этом меняться частота колебаний маятника?

Теперь увеличивайте или уменьшайте длину нити, на которой подвешен грузик. Наблюдайте, как будет меняться частота колебаний маятника.

Увеличивайте или уменьшайте массу подвешенного грузика. Будут ли меняться частота и амплитуда колебаний маятника?

 

Рис. 60. Иллюстрация к заданию 2

 

2. Натяните верёвку между двумя стойками и подвесьте к ней несколько верёвок разной длины с прикреплёнными к ним грузиками (рис. 60). Отведите в сторону один из грузиков и отпустите, заставив его свободно колебаться. Пронаблюдайте, как будут качаться остальные грузики

3. Рассмотрите рисунок 61 и объясните, как изображённый на фотографии мост через Волгу связан с понятием резонанса.

 

Рис. 61. Мост через Волгу

 

Волны

 

 

Набегают волны синие.

Зелёные? Нет, синие.

Как хамелеонов миллионы,

Цвет меняя на ветру.

 

Вот передо мною море голубое,

Плещет волна, волна.

Знаю, о чём, о чём

Шепчет она, она.

Шепчет она о том, что нет предела

Снам и мечтам, мечтам.

И всё зовёт, зовёт

К дальним местам, местам.

 

Н. Матвеева

 

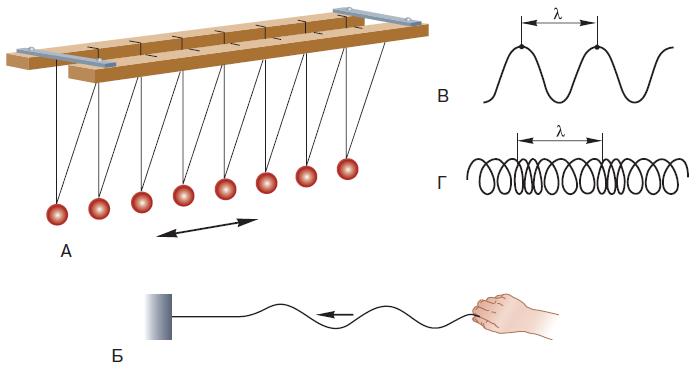
Представим себе, что рядом с математическим маятником находится другой точно такой же маятник (рис. 62, А). Плоскости, в которых качаются маятники, совпадают. Отведём первый маятник в направлении, противоположном тому, где находится второй, и отпустим его. Маятник начнёт движение, пройдёт точку равновесия и заденет соседний маятник, передав ему свой импульс.

 

Рис. 62. Волны: А – продольные; Б – поперечные.

Длина волны (λ) – это расстояние между ближайшими горбами или впадинами поперечной волны (В) или расстояние между ближайшими сгущениями или разрежениями продольной волны (Г)

 

В этом случае происходит упругое столкновение, при котором тела не слипаются, а отскакивают в противоположных направлениях. Приобретя импульс, второй маятник начнёт своё собственное качание, а первый после удара будет двигаться в противоположном направлении. Получается, что второй маятник проделает точно такое же колебательное движение, что и первый, но только с запаздыванием. Теперь вообразим, что за вторым маятником находится третий, за ним четвёртый и т. д. Последовательно толкая друг друга, со временем все они будут колебаться с одинаковой частотой и амплитудой, но каждый из них будет совершать своё колебание через некоторое время после предыдущего. Первый маятник, вернувшись после столкновения со вторым в исходное положение, начнёт новое колебание, и весь процесс повторится. Такое явление, в котором колебания последовательно передаются из одних точек пространства в другие, называют волной.   Можно сказать, что волна представляет собой колебание, распространяющееся в пространстве. Если система маятников или другая волновая система является идеальной, т. е. в ней не действуют силы, мешающие движению, то волны по ней пройдут от первого до последнего маятника, не изменяя амплитуды. Это означает, что такая волна распространяется без затухания, т. е. является незатухающей.   В реальной системе чем дальше от первого маятника находится другой маятник, тем слабее будут его колебания, пока на большом расстоянии они совсем не исчезнут. Такую волну называют затухающей.  

Допустим, что мы имеем дело с незатухающей волной, и посмотрим, как она выглядит в каждый момент времени. Последовательно рассматривая её отдельные участки, мы увидим, что в некоторых из них соседние маятники находятся близко друг от друга, так как они только что столкнулись или вот-вот столкнутся. В других местах мы увидим, что расстояние между ними достаточно велико, так как один из них в этот момент продвинулся максимально вперёд, а другой максимально назад от точки равновесия. Если теперь построить график, где по всей длине нашей системы будут обозначены расстояния между соседними маятниками, то получится линия, которая описывается синусоидой. Такую форму колебаний называют гармонической (см. § 21).

 

Продольные волны.

 

В природе, однако, распространены не системы из искусственно сделанных грузиков на нити, а естественные системы, состоящие из молекул, атомов и элементарных частиц. В этих случаях размер колеблющихся предметов и расстояния между каждой их парой очень малы по сравнению с расстоянием, на которое распространяется волна, а число этих объектов таково, что измерить все расстояния невозможно. В таких системах построить график движения волны можно другим способом. Возьмём маленькие отрезки одинаковой длины, последовательно расположенные вдоль линии, по которой распространяется волна, и подсчитаем, сколько точек находится на каждом из них. Это число будем называть плотностью точек на данном отрезке. Мы убедимся в том, что на некоторых участках плотность будет небольшой (такие участки называют областью разрежения), а на некоторых значительно большей (эти участки называют областью сгущения). Если мы отложим на графике значения плотности в каждом участке линии, то увидим, что она колеблется в соответствии с тем же гармоническим синусоидальным законом.

Такие волны, в которых частицы тела колеблются в направлении распространения волны, называют продольными волнами   или волнами сжатия.  

 

Поперечные волны

 

Наряду с продольными существуют поперечные волны,   в которых частицы колеблются перпендикулярно направлению распространения волны. Наблюдать поперечную волну проще всего, если привязать к чему-нибудь верёвку, а затем взяться за её свободный конец и качнуть (рис. 62, Б). По верёвке побежит волна, в которой со строгой регулярностью во времени и пространстве будут чередоваться горбы и впадины. Если качать конец верёвки в течение некоторого времени с постоянной частотой, волны будут постоянно распространяться по ней от вашей руки до того места, где верёвка закреплена. Это происходит потому, что в верёвке, как и во всяком твёрдом теле[8], существуют силы сцепления между молекулами, которые называются силами упругости. Первая качнувшаяся молекула тянет за собой вторую, вторая – третью и т. д. В принципе весь процесс напоминает тот, который происходит при последовательном колебании маятников с той разницей, что колебания происходят не в направлении движения волны, а перпендикулярно ей.

Проще всего наблюдать волны на воде, будь то большие морские волны, мелкая рябь на пруду или реке или расходящиеся круги от брошенного в лужу камня. Понаблюдав за такими волнами, мы увидим, что в некоторых местах вода приподнята над неким средним уровнем, а в других находится ниже его. Эта картина пребывает в постоянном движении: там, где только что была выпуклость, появляется впадина, и наоборот. Такие волны не подчиняются простым законам, они представляют собой сложную комбинацию продольных и поперечных волн. Форма волны и характер её движения также зависят от глубины водоёма и некоторых других причин (рис. 63, 64).

Необходимо иметь в виду, что среда, в которой распространяются волны, сама никуда не движется. В этом легко убедиться, понаблюдав за каким-либо предметом, находящемся на поверхности воды.

 

Рис. 63. Кацусика Хокусай. Большая волна в Канагаве. 1823–1831 (Метрополитен-музей, Нью-Йорк)

 

После того как в воду бросили камень, предмет начнёт колебаться вверх и вниз, но его расстояние до берега при этом не изменится. Однако это касается только простого волнового движения. В более сложных случаях колебание может складываться с движением самой среды. Примером такого сложного движения является морской прибой.