Периодическое движение: вращение и колебание

 

Пока я смотрел прямо вверх (маятник приходился как раз надо мною), мне почудилось, что он двигается. Минуту спустя впечатление подтвердилось. Ход маятника был короткий и, разумеется, медленный. Несколько мгновений я следил за ним с некоторым страхом, но скорей с любопытством. Наконец, наскуча его унылым качанием, я решил оглядеться.

Э. По. Колодец и маятник

 

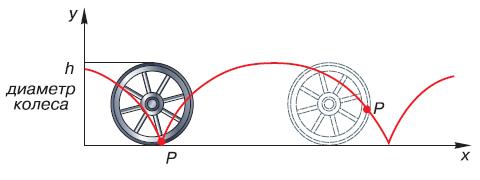
Теперь познакомимся с тем, что происходит, если тело движется прямолинейно и одновременно с этим участвует во вращательном движении. Представьте себе, что катится колесо. Мы уже говорили, что при этом его единственная точка, а именно центр, движется прямолинейно, а остальные, наряду с этим поступательным движением, движутся по окружности вокруг этого центра. Какие траектории будут описывать эти точки, например точка, находящаяся на ободе колеса? Рассмотрим это на графике, где по оси x отложим положение точки относительно места начала её движения, а по оси у – её высоту над землёй (рис. 55). Мы видим, что эта высота меняется в пределах от нуля до размеров диаметра колеса. По мере того как колесо катится всё дальше, высота положения точки на его ободе постепенно повышается, затем начинает плавно снижаться до нуля и снова постепенно повышаться. Такое движение называют периодическим.  

 

Вращение.

 

Для того чтобы наблюдать периодические движения, необязательно, чтобы тела передвигались в пространстве вдоль прямой линии. В некоторых случаях достаточно, чтобы они просто вращались. В этом легко убедиться, посмотрев на обычные часы. Их стрелки вращаются вокруг оси, и при этом мы замечаем, что они периодически возвращаются в одну и ту же точку циферблата. Можно построить график, аналогичный предыдущему, но теперь по оси x отложить уже не расстояние, а время. По оси у отложим цифры, на которые указывает стрелка. Правда, может возникнуть проблема: как измерять отрезки времени? Этого нельзя сделать по нашим часам, поскольку с их помощью мы измеряем движение стрелок самих часов.

 

Рис. 55. Траектория движения точки оси и обода колеса при его качении

 

Для этой цели нужно воспользоваться другими часами, например песочными. Также можно считать свой пульс, как это делал Галилей, или просто довериться внутреннему ощущению времени, о котором мы говорили в предыдущей главе. В любом случае мы знаем, что время проходит, правильнее сказать, длится. И по мере того как оно длится, стрелки на циферблате часов меняют своё положение от 1 до 12, снова от 1 до 12 и так всё время, пока мы будем наблюдать. Но если часы имеют три стрелки – часовую, минутную и секундную, то они будут возвращаться в исходное положение, скажем, к цифре 1, через неодинаковое время. Секундной стрелке для этого понадобится 60 с, минутной – час, т. е. 3600 с, а часовой – 12 ч, т. е. 43 200 с. Это означает, что разные стрелки имеют различные периоды обращения, которые равны соответственно минуте, часу и 12 часам. Такое движение называют периодическим,   и мы его уже обсуждали в предыдущем параграфе. По завершении цикла – полного оборота стрелки – она возвращается в исходное положение, и всё начинается сначала. Но это начало будет началом только с точки зрения этой стрелки, а с точки зрения других – процесс будет продолжаться. Если у нас есть часы с разными стрелками, мы можем не пользоваться для отсчёта никакими другими часами, а просто построить график, отложив по оси х показания минутной стрелки, а по оси у – секундной. Ровно через минуту секундная стрелка вернётся в исходное положение и начнёт отсчёт сначала, а минутная сдвинется только на одно деление и будет отсчитывать всё новые отрезки времени. Посмотрев на график, мы увидим, что на нём изображена периодическая функция. Через равные отрезки на оси х, соответствующие минуте, точка будет иметь одинаковые значения, если отсчитывать их по оси х. Мы получили периодическое   движение с периодом, составляющим 1 мин.

Под периодическими процессами понимают такие изменения в системах, когда их положение или состояние через определённый промежуток времени возвращается к тому, которое уже имело место раньше. Самым наглядным периодическим процессом служит движение Земли вокруг своей оси и вокруг Солнца. С интервалом в 24 ч Солнце появляется над горизонтом, проходит через зенит и исчезает за другой точкой горизонта. С интервалом приблизительно в 365 дней меняется температура воздуха, распускаются и опадают листья, празднуется день рождения, начинается и кончается учебный год. Но эти примеры хотя и наглядны, но не совсем точны. Солнце сегодня восходит и заходит не совсем в тех точках, где оно это делало вчера, листья в этом году могут распуститься раньше или позже, чем в предыдущем, да и вообще Земля оборачивается вокруг Солнца не за 365 дней, а несколько медленнее. Так что такая периодичность, в отличие от периодичности точных физических процессов, имеет приблизительный характер. Но именно чередование времени суток и времён года послужило для человечества началом измерения времени, создания календаря и внесло порядок в хозяйственное и социальное устройство.

 

Колебания.

 

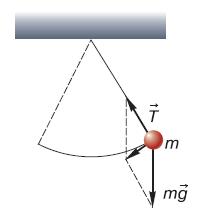
Периодические процессы также называют колебательными движениями   или просто колебаниями  . Наиболее наглядно колебательное движение можно представить при помощи маятника. Движение маятника является примером механического колебательного движения. Обычный маятник представляет собой груз, подвешенный на нити (математический маятник) или прикреплённый к пружине (пружинный маятник). Математический маятник называется так потому, что при изучении его колебаний приходится, как это бывает всегда в математической физике (вспомним Галилея), чем– нибудь пренебрегать. В данном случае пренебрегают размером подвешенного тела и весом нити, на которой оно подвешено. Считается, что размер самого тела намного меньше длины нити, а его вес намного больше её веса. В идеале тело вообще не имеет размеров и представляет собой бесконечно малую точку, а нить абсолютно невесома. Так, конечно, не бывает, но для расчётов такая модель очень удобна.

Математический маятник.   Процесс колебания математического маятника выглядит следующим образом (рис. 56). Отведём груз на некоторое расстояние. Тогда на него будет действовать сила тяжести, направленная вертикально вниз, и сила натяжения нити. В результате сложения этих сил груз будет совершать движение по дуге. Оказавшись в самой низкой точке, он достигнет положения равновесия. Но он не останавливается, а по инерции продолжает своё движение по дуге, но уже поднимаясь вверх. Так как ускорения во время снижения и во время подъёма равны по модулю, высота этой точки будет в точности равна той, с которой маятник начал своё снижение. Поэтому весь процесс движения повторяется, но в обратном направлении. При отсутствии трения эти колебания будут продолжаться бесконечно.

Пружинный маятник.   Пружинный маятник похож по принципу действия на математический, но вместо гравитации в нём действует сила упругости пружины. Если закрепить груз на горизонтальной пружине, а затем эту пружину растянуть, то сила упругости будет пропорциональна удлинению пружины (рис. 57). Под действием этой силы груз начнёт двигаться вверх к положению равновесия. Но, дойдя до точки равновесия, он не остановится, а будет по инерции продолжать двигаться в противоположную сторону, сжимая пружину. Упругая сила сжимаемой пружины сначала остановит груз, а потом заставит его двигаться в обратном направлении, пока он не вернётся в исходную точку.

 

Рис. 56. Разложение сил при колебании маятника

 

Там на груз опять будет действовать сила растянутой пружины, и колебательный процесс будет продолжаться.