
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод адиабатического расширенияСодержание книги
Поиск на нашем сайте
Экспериментальная установка (рис.1) состоит из баллона Б объемом
где Рассмотрим термодинамические процессы, происходящие с воздухом, заключенным в баллон.
Сжатие воздуха в баллоне. Краном К соединяют баллон с резиновой грушей и накачивают воздух до давления, соответствующего разности уровней жидкости h в манометре, равной 15-20 делений шкалы, после чего кран закрывают. При сжатии газ нагревается. Необходимо выждать не менее 3-5 минут, чтобы газ в баллоне охладился до комнатной температуры
где Адиабатное расширение. Поворотом крана К на короткое время соединяют баллон с атмосферой. Как только давление в баллоне станет равным атмосферному, о чем судят по показаниям манометра (h =0), кран закрывают. Поскольку процесс расширения происходит быстро, теплообмен между содержимым баллона и окружающим воздухом не происходит, т.е. наблюдается адиабатное расширение, сопровождающееся понижением температуры. В конце процесса расширения воздух в баллоне имеет давление
Изохорическое нагревание. Закрыв кран К, следует дождаться, когда установится тепловое равновесие воздуха в баллоне и окружающей среде. Момент установления равновесия фиксируется по прекращению перемещения уровней жидкости в коленах манометра. В этот момент состояние воздуха в баллоне характеризуется температурой
где Согласно закону Гей-Люссака:
Исключив из (5) и (7) температуры
Логарифмируя обе части соотношения (8), находим:
Разложим C учетом разложения в ряд расчетная формула приобретает вид:
Метод стоячих звуковых волн
Одним из методов определения
В выражении (11) произведение
где Е − модуль Юнга, а − плотность вещества. По закону Гука изменение длины тела В случае газа величины где P − изменение давления газа. При увеличении давления газа, соответственно уменьшается его объем. Поэтому:
Вследствие адиабатичности звуковых процессов, объем и давление газа связаны уравнением Пуассона:
Из него, вследствие дифференцирования, легко установить, что
Сравнивая (15) и (13) и, воспользовавшись уравнением (12), получим уравнение (11). Если из уравнения Менделеева-Клапейрона найти плотность газа и это значение подставить в выражение (11), то получим, что
где М − молярная масса газа, R − газовая постоянная. Последнее выражение позволяет определить, если известны с, М, R, T. В данной работе скорость звука определяется методом стоячих звуковых волн − методом Кундта. Известно, что
где l − расстояние между двумя соседними максимумами, Используя соотношение (17), выражение (16) можно переписать в виде:
Порядок выполнения работы
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.95 (0.01 с.) |

 , который с помощью крана К может быть соединен либо с резиновой грушей Г, либо с атмосферой. Разность давлений воздуха в баллоне и в окружающей среде измеряется открытым жидкостным манометром М, заполненным водой или каким-либо маловязким маслом. Разность уровней жидкости в коленах манометра прямо пропорциональна разности давлений воздуха в баллоне и в окружающей среде:
, который с помощью крана К может быть соединен либо с резиновой грушей Г, либо с атмосферой. Разность давлений воздуха в баллоне и в окружающей среде измеряется открытым жидкостным манометром М, заполненным водой или каким-либо маловязким маслом. Разность уровней жидкости в коленах манометра прямо пропорциональна разности давлений воздуха в баллоне и в окружающей среде: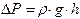 ,
,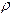 − плотность манометрической жидкости, g − ускорение свободного падения, h − разность уровней жидкости в коленах манометра.
− плотность манометрической жидкости, g − ускорение свободного падения, h − разность уровней жидкости в коленах манометра.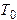 . При установлении равновесия между газом в баллоне и окружающей средой давление в баллоне перестанет изменяться и прекращается изменение уровней жидкости в манометре. В конце первого этапа состояние воздуха в баллоне характеризуется температурой
. При установлении равновесия между газом в баллоне и окружающей средой давление в баллоне перестанет изменяться и прекращается изменение уровней жидкости в манометре. В конце первого этапа состояние воздуха в баллоне характеризуется температурой 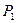 :
: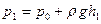 , (4)
, (4)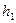 − установившаяся разность уровней манометрической жидкости в конце этапа.
− установившаяся разность уровней манометрической жидкости в конце этапа.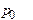 и температуру
и температуру 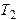 . Изменение параметров состояния газа при совершении адиабатического процесса описывается уравнением Пуассона:
. Изменение параметров состояния газа при совершении адиабатического процесса описывается уравнением Пуассона: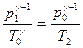 . (5)
. (5)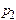 :
: 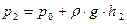 , (6)
, (6)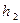 − установившаяся разность уровней жидкости в манометре в конце процесса нагревания.
− установившаяся разность уровней жидкости в манометре в конце процесса нагревания.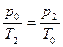 . (7)
. (7)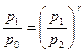 . (8)
. (8) 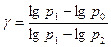 . (9)
. (9)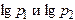 в ряд Тейлора, ограничившись первыми двумя членами ряда, поскольку, как уже было сказано, изменение давления воздуха в баллоне весьма невелико по сравнению с
в ряд Тейлора, ограничившись первыми двумя членами ряда, поскольку, как уже было сказано, изменение давления воздуха в баллоне весьма невелико по сравнению с 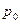 :
: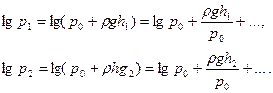
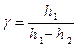 . (10)
. (10)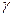 является метод стоячих звуковых волн. Этот точный метод основан на измерении скорости звука в газе. Из акустики известно, что скорость звука
является метод стоячих звуковых волн. Этот точный метод основан на измерении скорости звука в газе. Из акустики известно, что скорость звука 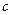 , плотность газа
, плотность газа 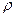 и давление
и давление 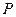 связаны между собой соотношением:
связаны между собой соотношением: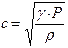 . (11)
. (11)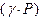 играет роль модуля объемной упругости газа. Это соотношение может быть получено из известной формулы, определяющей скорость распространения звука в твердом теле:
играет роль модуля объемной упругости газа. Это соотношение может быть получено из известной формулы, определяющей скорость распространения звука в твердом теле: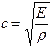 , (12)
, (12)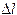 пропорционально изменению напряжения P:
пропорционально изменению напряжения P: 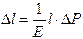 .
.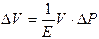 ,
,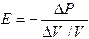 . (13)
. (13)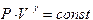 . (14)
. (14) 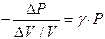 . (15)
. (15)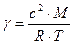 , (16)
, (16)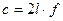 , (17)
, (17)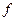 − частота звуковых колебаний.
− частота звуковых колебаний.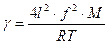 . (18)
. (18)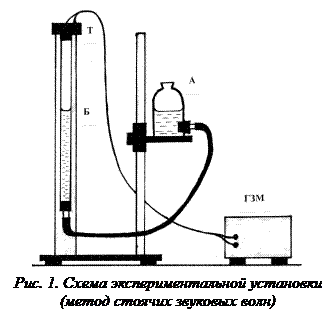 Экспериментальная установка, позволяющая определить величину
Экспериментальная установка, позволяющая определить величину 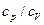 методом стоячих звуковых волн, представляет собой систему сообщающихся сосудов А и Б (рис.2). В верхней части сосуда Б расположен телефон Т (мембрана обращена внутрь трубки), который соединяется со звуковым генератором ГЗМ. Стетоскоп С, соединенный с сосудом Б, служит для определения на слух максимального звучания воздушного столба в трубке Б (резонанса), что позволяет найти l.
методом стоячих звуковых волн, представляет собой систему сообщающихся сосудов А и Б (рис.2). В верхней части сосуда Б расположен телефон Т (мембрана обращена внутрь трубки), который соединяется со звуковым генератором ГЗМ. Стетоскоп С, соединенный с сосудом Б, служит для определения на слух максимального звучания воздушного столба в трубке Б (резонанса), что позволяет найти l.


