
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов измеренийСодержание книги
Поиск на нашем сайте
1. По данным таблицы построить диаграмму плавления и кристаллизации исследуемого металла, откладывая по горизонтальной оси время 2. По диаграмме определить температуры плавления и кристаллизации исследуемого образца. 3. Выделить на диаграмме примерно прямолинейные участки до и после фазового перехода (плавление). По полученным данным определить среднюю скорость нагревания металла Проделать то же самое для охлаждения металла. 4. По формуле (3) рассчитать удельную теплоту 5. По формуле (8) рассчитать изменение энтропии 6. Найти удельную теплоемкость олова, считая, что количество теплоты, ежесекундно подводимое к тиглю, постоянно. Теплоемкость тигля и потери теплоты в окружающее пространство считать бесконечно малыми. 7. Оценить погрешность результатов измерений. 8. Полученные результаты эксперимента и расчета погрешности представить в виде таблицы:
Контрольные вопросы: 1. Какие фазовые переходы называются фазовыми переходами первого рода? 2. Почему температура плавления и кристаллизации остается постоянной? 3. Что называется удельной теплоемкостью вещества? 4. Что называется удельной теплотой фазового перехода? 5. Что такое энтропия? Сформулировать закон возрастания энтропии.
Литература: 1. Фриш, С.Э. Курс общей физики: учебник: [в 3 т.]. Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны / С.Э. Фриш. – 13-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2009. – 480 с.: ил. 2. Савельев, И.В. Курс общей физики: учебное пособие для вузов [в 3 т.]. Т. 1. Механика. Молекулярная физика / И.В. Савельев. – 10-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2008. – 432 с.: ил. 3. Трофимова, Т.И. Основы физики: учебное пособие: в 5 кн. Кн.2. Молекулярная физика. Термодинамика / Т.И. Трофимова. – Москва: Высшая школа, 2007. – 180 с.: ил. 4. Пронин, Б.В. Физика [Электронный ресурс]: учебник / Б.В. Пронин. – Москва: Издательство РГАУ-МСХА имени К.А. Тимирязева, 2012. – 445 с. – Режим доступа:
http://biblioclub.ru/index.php?page=book&id=144822
ЛАБОРАТОРНАЯ РАБОТА № 9
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЁМКОСТИ ТВЕРДЫХ ТЕЛ Цель работы: проверка выполнимости закона Дюлонга и Пти для ряда исследуемых твердых тел.
Краткая теория Согласно классической теории теплоемкости при не слишком низких температурах, молярная теплоемкость химически простых веществ в кристаллическом состоянии одинакова и равна 25 Между частицами, образующими кристаллическую решетку твердых тел, существуют силы взаимодействия. Расположение частиц в узлах кристаллической решетки отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в первоначальное положение, вследствие чего возникают её колебания. При точном рассмотрении задачи необходимо учитывать, что частицы в решетке взаимодействуют друг с другом и их колебания надо рассматривать как связанные. Однако, при достаточно высоких температурах, когда энергия становится большой, колебания частиц можно рассматривать приближенно как независимые друг от друга. Полная энергия частицы U равна сумме кинетической Ек и потенциальной Еп:
Колебания частиц в узлах кристаллической решетки приближенно являются гармоническими. При этом как кинетическая, так и потенциальная энергии гармонических колебаний частицы являются периодическими функциями времени и их средние значения С другой стороны, из кинетической теории идеального газа известно, что средняя кинетическая энергия одноатомных молекул (изолированных частиц) где k - постоянная Больцмана, Т – абсолютная температура. Поскольку, как было отмечено, атомы или ионы кристаллической решетки при достаточно высоких температурах колеблются независимо друг от друга, к ним также применима формула (2). Тогда из (1) и (2) имеем
Полную внутреннюю энергию одного моля твердого тела получим умножением средней энергии одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле, т.е. на постоянную Авогадро NА: где R – молярная газовая постоянная.
Для твердых тел вследствие малого коэффициента теплового расширения теплоемкости при постоянном давлении и постоянном объеме практически не различаются. Поэтому общее выражение теплоемкости твердого тела совпадает со значением молярной теплоемкости при V = const:
Из формулы (4) окончательно следует, что
Подставляя численное значение молярной газовой постоянной, получаем: Это равенство выполняется с довольно хорошим приближением для многих веществ при комнатной температуре. В области низких температур наблюдается отклонение (рис.1). Вблизи абсолютного нуля молярная теплоемкость всех тел пропорциональна Т3, и только при достаточно высокой, характерной для каждого вещества температуре, начинает выполняться равенство (5). Строгая теория теплоемкости твердых тел создана А. Эйнштейном и П. Дебаем. Она учитывает, что колебания частиц в кристаллической решетке не являются независимыми и что энергия колебательного движения квантована.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.103 (0.009 с.) |

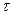 в минутах, а по вертикальной оси – температуру t в 0С.
в минутах, а по вертикальной оси – температуру t в 0С.
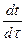
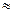
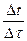 =
= 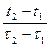 .
.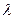 плавления и кристаллизации исследуемого металла. В качестве исследуемого металла используется олово. Масса металла (олово) m
плавления и кристаллизации исследуемого металла. В качестве исследуемого металла используется олово. Масса металла (олово) m 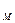 = 61, 26г; масса тигля (железо) m
= 61, 26г; масса тигля (железо) m 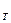 =38, 25г. Значения удельных теплоемкостей с
=38, 25г. Значения удельных теплоемкостей с 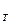 взять из справочника.
взять из справочника.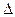 S при нагревании и плавлении олова.
S при нагревании и плавлении олова.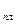 , K
, K
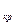 ,K
,K
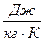
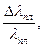 %
%
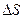 ,
, 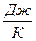
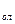 ,
, 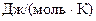 . Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем.
. Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем.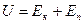 .
.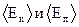 равны друг другу:
равны друг другу: 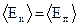 . Поэтому среднее значение полной энергии
. Поэтому среднее значение полной энергии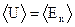 . (1)
. (1)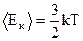 , (2)
, (2)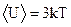 . (3)
. (3)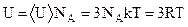 , (4)
, (4)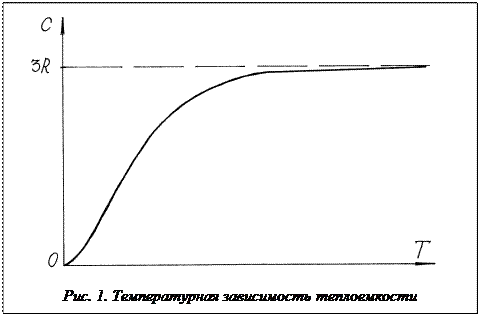
 .
.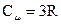 .
.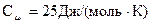 . (5)
. (5)


