
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности косвенных измерений
Большинство физических величин определяется косвенными путями. Сначала производится непосредственное измерение одной или нескольких физических величин, количественно связанных с определяемой, а затем, с помощью соответствующих формул вычисляется значение определяемой величины. Очевидно, при этом ошибка вычисления определяемой величины зависит от величины погрешностей непосредственных измерений исходных величин. Абсолютная ошибка функции одного переменного равна абсолютной ошибке аргумента, умноженной на первую производную этой функции. Относительная погрешность получится, если мы обе части равенства разделим на значение определяемой величины y: Как видно, в правой части равенства стоит дифференциал от натурального логарифма функции f(x), следовательно, Относительная ошибка вычисления функции одного переменного равна дифференциалу натурального логарифма этой функции. В качестве примера вычислим ошибку в определении объема шара по измеренному радиусу. Пусть радиус шара:
Объем шара подсчитывается по формуле:
Тогда, абсолютная ошибка вычисления объема шара:
Подставим численные значения:
Относительная ошибка:
Если измеряемая величина является функцией нескольких непосредственно измеренных величин:
Предельная абсолютная ошибка функции нескольких переменных равна сумме модулей произведений частных производных этой функции на соответствующие абсолютные ошибки.
где частные производные Предельная относительная ошибка функции нескольких переменных равна дифференциалу натурального логарифма этой функции, причем берется сумма абсолютных значений всех членов этого выражения. Пример:
Положим, объем параллелепипеда определяется по данным измерений его рёбер V = abc. Для расчета предельной ошибки вычисления объема найдем частные производные от V по a, b и c:
и выражение для абсолютной погрешности:
Для расчета относительной погрешности прологарифмируем V: ln V = ln a + ln b + ln c. Почленно дифференцируя и, переходя от дифференциалов к ошибкам, получим:
Измерительные инструменты Измерительная линейка - Линейку прикладывают к измеряемому предмету так, чтобы её 0 совпадал с началом измеряемой длины. Если концы линейки испорчены, то начало предмета прикладывают к любой отметке шкалы, затем от нее ведут отсчет. - Линейку нужно прикладывать ровно, а не наискось, во избежание неправильного измерения. - При наблюдении глаз должен быть расположен против наблюдаемой отметки. Штангенциркуль Штангенциркуль состоит из линейки со шкалой, имеющей миллиметровые деления, и нониуса – дополнительной линейки, которая может перемещаться вдоль шкалы. Нониус имеет 10 делений, которые равны 9 делениям шкалы, поэтому каждое деление нониуса короче деления шкалы на 0,1 и равно 0,9 мм. При сдвинутых щеках нулевая отметка нониуса совпадает с нулевой отметкой линейки, а десятая отметка – с 9-ой отметкой линейки. При этом 1-е деление нониуса не доходит до 1 - го деления линейки на 0,1 мм, а 2 – е деление нониуса до 2 – го деления линейки на 0,2 мм и т.д. Если первая отметка нониуса совпадает с 1-ой отметкой линейки, то между ними образуется просвет 0,1 мм. Если совпадают вторые отметки, то просвет 0,2 мм и т.д. Следовательно, отметка нониуса, совпадающая с отметкой линейки, указывает расстояние между щеками в десятых долях миллиметра. Правила пользования При измерении длины тела его зажимают между щеками штангенциркуля. Отсчет целых делений (мм) проводят по шкале линейки до нуля нониуса, затем отсчитывают по нониусу десятые доли миллиметра, число которых равно номеру штриха на нониусе, совпадающему со штрихом основной шкалы. Микрометр. Основные части – стальная скоба и втулка, имеющая с внутренней стороны микрометрическую резьбу, а на поверхности – шкалу с делениями 0,5 мм и продольную черту.
Во втулку ввертывается микрометрический винт. На правый конец винта насажена гильза, имеющая 50 делений. При вращении винта вращается и гильза. С правой стороны винта ввертывается «трещотка», с помощью которой производится передвижение винта во втулке. «Трещотка» регулирует нажим на измеряемое тело. На левом конце скобы находится упорная щека – наковаленка. Шаг винта микрометра равен 0,5 мм. Число делений на гильзе равно 50, и, следовательно, от поворота гильзы на одно деление винт отходит от щеки на 0,01 мм; при двух оборотах гильзы последняя проходит 100 делений, и винт отодвигается от щеки на 1 мм. - Точная, окончательная установка винта при измерении производится «трещоткой», иначе можно испортить нарезку микровинта. - Не следует пользоваться микрометром с застопоренным фиксатором.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.190.144 (0.007 с.) |
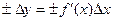 . (8)
. (8)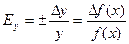 . (9)
. (9)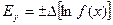 . (10)
. (10)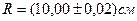 ;
;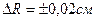 ;
; 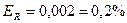 .
.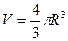 .
.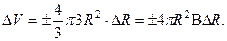
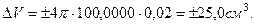
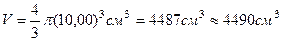 или
или 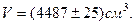
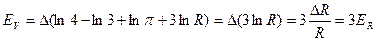 ,
,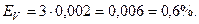
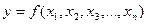 .
.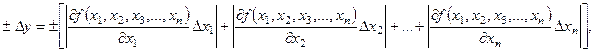 (11)
(11)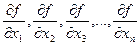 вычисляются как для обычной функции одной переменной (соответственно
вычисляются как для обычной функции одной переменной (соответственно 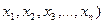 в предположении, что все остальные аргументы принимают постоянные значения.
в предположении, что все остальные аргументы принимают постоянные значения.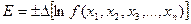 (12)
(12)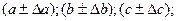
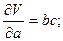
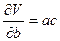 ;
; 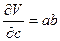
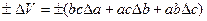 .
.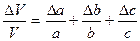 .
.


