
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярная физика и термодинамикаСтр 1 из 22Следующая ⇒
ЛАБОРАТОРНЫЙ ПРАКТИКУМ МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Вологда 2016
УДК 539.1:536(076).5 ББК 22.36я73+22.317.1я73 М 75 (или П 43)
Погожев, С.Э. Молекулярная физика и термодинамика: Лабораторный практикум. / С.Э. Погожев. – Вологда: ВоГУ, 2016. – 68 с.
Пособие содержит описание лабораторного практикума, включая краткую теорию, методические указания по выполнению работ, описание лабораторных установок, рекомендуемую литературу и контрольные вопросы к защите. Пособие предназначено для студентов направления бакалавриата 44.03.05 – Педагогическое образование, направленности (профиля) – Математическое и физическое образование и может быть использовано студентами других направлений, изучающих курс физики.
© ВоГУ, 2016 © Погожев С.Э., 2016 Содержание
ВВЕДЕНИЕ Физика – наука экспериментальная. Это означает, что физические законы устанавливаются и проверяются путем накопления и сопоставления экспериментальных данных. Поэтому лабораторные занятия по физике преследуют две основные цели: во-первых, дать возможность студентам познакомиться с наиболее важными приборами и овладеть основными методами точных физических измерений, вырабатывая тем самым практические навыки научного исследования. Во-вторых, дать возможность более подробно ознакомиться с некоторыми явлениями и законами природы, для полного понимания которых одних демонстрационных опытов на лекциях по физике, как правило, бывает недостаточно. В лабораторный практикум включены описания лабораторных работ по разделу курса общей и экспериментальной физики: молекулярная физика и термодинамика. В каждой работе изложены цель, основные положения теории, описание лабораторной установки, порядок выполнения работы и обработки результатов, рекомендуемая литература, контрольные вопросы для защиты полученных результатов. Кроме того, в приложении к данному практикуму представлены некоторые элементы физических измерений, которые необходимы при расчетах погрешностей измерений. При подготовке к выполнению очередной лабораторной работы необходимо изучить теоретический материал, изложенный в рекомендуемой литературе, список которой представлен после описания каждой работы. При работе в лаборатории необходимо строго соблюдать правила техники безопасности.
ЛАБОРАТОРНАЯ РАБОТА № 1
Определение величины отношения теплоемкостей воздуха при постоянном давлении и постоянном объеме
Цель работы: определение величины отношения теплоемкостей воздуха при постоянном давлении и постоянном объеме методом адиабатического расширения и методом стоячих звуковых волн.
Краткая теория Удельной теплоемкостью называется физическая величина, численно равная количеству теплоты, которое необходимо затратить для изменения температуры тела массой 1 кг на 1 К:
где dQ − количество теплоты, сообщенное телу; dT − изменение температуры тела. Теплоемкость тела зависит от его массы. В молекулярной физике чаще всего оперируют понятием молярной теплоемкости, т.е. теплоемкости одного моля вещества. Молярная теплоемкость измеряется в Дж/(моль К).
Численное значение теплоемкости зависит от условий, при которых телу сообщалось тепло, поскольку тело, нагреваясь, как правило, изменяет свой объем, т.е. производит работу против сил внешнего давления. Согласно первому закону термодинамики, эта работа может быть совершена либо за счет изменения его внутренней энергии, либо за счет теплоты, полученной телом извне. Рассмотрим изохорический процесс нагревания тела. В этом случае расширения не происходит, работа против внешних сил равна нулю и вся подводимая к телу теплота затрачивается только на изменение его внутренней энергии:
где dU − изменение внутренней энергии тела; m − масса тела; Нагревание тела в изобарических условиях сопровождается изменением объема тела, т.е. совершением им работы расширения. В этом случае:
или
где Очевидно, молярная теплоемкость при постоянном давлении
Соотношение (1) называется уравнением Роберта Майера и справедливо только для идеального газа. В данной работе измеряются не сами теплоемкости воздуха
Это связано с тем, что экспериментальное определение изохорической теплоемкости газа весьма затруднительно, в то время как это ее значение легко вычислить, зная отношение теплоемкостей
или для идеального газа:
Метод стоячих звуковых волн
Одним из методов определения
В выражении (11) произведение
где Е − модуль Юнга, а − плотность вещества. По закону Гука изменение длины тела В случае газа величины где P − изменение давления газа. При увеличении давления газа, соответственно уменьшается его объем. Поэтому:
Вследствие адиабатичности звуковых процессов, объем и давление газа связаны уравнением Пуассона:
Из него, вследствие дифференцирования, легко установить, что
Сравнивая (15) и (13) и, воспользовавшись уравнением (12), получим уравнение (11). Если из уравнения Менделеева-Клапейрона найти плотность газа и это значение подставить в выражение (11), то получим, что
где М − молярная масса газа, R − газовая постоянная. Последнее выражение позволяет определить, если известны с, М, R, T. В данной работе скорость звука определяется методом стоячих звуковых волн − методом Кундта. Известно, что
где l − расстояние между двумя соседними максимумами, Используя соотношение (17), выражение (16) можно переписать в виде:
Порядок выполнения работы Метод стоячих звуковых волн
1. Разобраться в назначении отдельных элементов экспериментальной установки, познакомиться со звуковым генератором. 2. Включить звуковой генератор, дать ему прогреться, установить определенную частоту 3. Поднимая или опуская сосуд А, т.е. изменяя уровень воды, добиться максимального звучания воздушного столба. Уровень воды в сосуде Б зафиксировать. Затем аналогично найти положение второго максимального звучания воздушного столба и определить l (расстояние между двумя максимумами). Для данной частоты опыт проделать не менее 3 раз. При определении для данной частоты взять среднее арифметическое значение 4. Опыт проделать с другими частотами (по заданию преподавателя).
5. Вычислить, абсолютную Таблица 2
Контрольные вопросы
1. Что означает внутренняя энергия идеального газа с точки зрения молекулярно-кинетической теории. 2. Дать определения удельной и молярной теплоемкостей. В каких единицах они измеряются и какова связь между ними? 3. Какой процесс называется адиабатическим? Чему равна работа при адиабатическом процессе? 4. Чему равна величина отношения 5. Вывести уравнение Р.Майера. В чем заключается физический смысл универсальной газовой постоянной? 6. Что такое степень свободы? Показать, что 7. Показать, что 8. Почему распространение звука происходит адиабатически? 9. Каковы источники ошибок в данной работе?
Литература
1. Фриш, С.Э. Курс общей физики: учебник: [в 3 т.]. Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны / С.Э. Фриш. – 13-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2009. – 480 с.: ил. 2. Савельев, И.В. Курс общей физики: учебное пособие для вузов [в 3 т.]. Т. 1. Механика. Молекулярная физика / И.В. Савельев. – 10-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2008. – 432 с.: ил. 3. Трофимова, Т.И. Основы физики: учебное пособие: в 5 кн. Кн.2. Молекулярная физика. Термодинамика / Т.И. Трофимова. – Москва: Высшая школа, 2007. – 180 с.: ил. 4. Пронин, Б.В. Физика [Электронный ресурс]: учебник / Б.В. Пронин. – Москва: Издательство РГАУ-МСХА имени К.А. Тимирязева, 2012. – 445 с. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=144822
ЛАБОРАТОРНАЯ РАБОТА № 2 Краткая теория
При движении слоев жидкости или газа с различными скоростями между слоями действуют силы внутреннего трения или силы вязкости. Численное значение силы вязкости можно определить по формуле Ньютона: где − коэффициент внутреннего трения или динамическая вязкость, S − площадь соприкасающихся слоев, Динамическая вязкость может быть выражена формулой: т.е. она численно равна силе внутреннего трения, возникающей между двумя слоями жидкости или газа, имеющими площадь соприкосновения, равную единице, при градиенте скорости, равном единице. В системе СГС динамическая вязкость измеряется в пуазах, а в СИ − в Пас. С точки зрения молекулярно-кинетической теории, динамическая вязкость численно равна количеству упорядоченного движения, переносимого за единицу времени через единицу площади соприкосновения слоев, при градиенте скорости, равном единице. Динамическая вязкость газов значительно меньше, чем у жидкостей.
Порядок выполнения работы
1. При закрытом кране В, наполнить баллон водой на 3/4 объема.
2. Открыть кран В и отрегулировать скорость истечения воды таким образом, чтобы разность уровней жидкости в коленах манометра не превышала 2-3 см. 3. Убедившись в том, что течение воздуха через капилляр установилось (в этом случае h остается неизменной), измерить h и с помощью секундомера определить время 4. Не изменяя разность уровней, измерить еще два раза время, в течение которого из баллона вытекает вода объемом v = 500 см 5. Изменив разность уровней, провести измерения, согласно п.3 и п.4, не менее 3 раз. 6. Вычислить значение динамической вязкости, средней длины свободного пробега, эффективного диаметра, среднюю абсолютную и среднюю относительную ошибки измерений. Результаты опытов и расчетов занести в таблицу 1. 7. Для того, чтобы установить было ли течение воздуха ламинарным, вычислить число Рейнольдса: где Средняя скорость: Замечание: если время вытекания одного и того же объема воды определяется при несколько отличающихся разностях давлений, усреднить это время нельзя. В этом случае динамическая вязкость рассчитывается три раза, а затем находится ее среднее значение. Таблица 1
Продолжение таблицы 1
Контрольные вопросы
1. Что называется эффективным диаметром газовых молекул? 2. Как зависит эффективный диаметр от температуры и давления? 3. Что называется длиной свободного пробега газовых молекул? 4. Как зависит длина свободного пробега от температуры и давления? 5. Что называется вязкостью газов, и от каких параметров она зависит? 6. Как объяснить различие температурной зависимости динамической вязкости газов и жидкостей? 7. Получить выражение для определения динамической вязкости газов методом истечения через капилляр? 8. Какие другие методы применяются для определения динамической вязкости жидкостей и газов? 9. Что называется кинематической вязкостью, и в каких единицах она измеряется? 10. Какое течение называется ламинарным? 11. Какой физический смысл имеет число Рейнольдса?
Литература
1. Фриш, С.Э. Курс общей физики: учебник: [в 3 т.]. Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны / С.Э. Фриш. – 13-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2009. – 480 с.: ил. 2. Савельев, И.В. Курс общей физики: учебное пособие для вузов [в 3 т.]. Т. 1. Механика. Молекулярная физика / И.В. Савельев. – 10-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2008. – 432 с.: ил. 3. Трофимова, Т.И. Основы физики: учебное пособие: в 5 кн. Кн.2. Молекулярная физика. Термодинамика / Т.И. Трофимова. – Москва: Высшая школа, 2007. – 180 с.: ил. 4. Пронин, Б.В. Физика [Электронный ресурс]: учебник / Б.В. Пронин. – Москва: Издательство РГАУ-МСХА имени К.А. Тимирязева, 2012. – 445 с. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=144822
ЛАБОРАТОРНАЯ РАБОТА № 3
ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ Цель работы: определение коэффициента поверхностного натяжения воды методом отрыва кольца и методом отрыва капель. Исследование температурной зависимости коэффициента поверхностного натяжения методом измерения максимального избыточного давления в пузырьках воздуха. Краткая теория
Молекулы поверхностного слоя жидкости испытывают действие не скомпенсированных межмолекулярных сил, направленных внутрь жидкости. Поэтому при переходе из внутренних частей жидкости на ее поверхность молекулы должны совершить работу против этих сил, что приводит к увеличению их потенциальной энергии по сравнению с остальными молекулами жидкости. В результате любое жидкое тело, на которое действуют внешние силы, должно принять форму, при которой площадь ее поверхности будет минимальной. Этому условию удовлетворяют тела сферической формы. Силы поверхностного натяжения в жидкостях не зависят от размеров свободной поверхности, т.е. стремятся сократить поверхность до нуля. Это свойство жидких пленок объясняется тем, что при изотермическом изменении величины поверхности жидкости изменяется число молекул, содержащихся в поверхностном слое, а среднее расстояние между молекулами не меняется. Поэтому не изменяются и силы межмолекулярного взаимодействия, определяющие величину поверхностного натяжения. Коэффициентом поверхностного натяжения называется величина работы, необходимой для образования единицы площади поверхности при постоянной температуре. Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность. Коэффициент поверхностного натяжения есть величина, численно равная свободной энергии единицы площади поверхности жидкости.
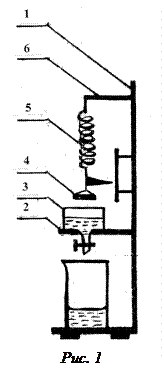
Метод отрыва кольца
Экспериментальная установка представлена на рис.1. Она состоит из деревянного штатива (1), на столике (2) которого закреплен сосуд (3) с исследуемой жидкостью. Тонкое металлическое кольцо (4) подвешено к пружине динамометра (цена деления шкалы динамометра – 40 мг) (5), верхний конец которой закреплен в подвижном кронштейне (6). Суть данного метода заключается в измерении силы, которую нужно приложить, чтобы оторвать кольцо от поверхности жидкости. Пусть
где d − толщина стенок кольца.
Метод отрыва капель
Установка для определения коэффициента поверхностного натяжения методом отрыва капель (рис.2) состоит из стеклянного сосуда (1) с краном (2) и тонкой полиэтиленовой трубки (3). При вытекании жидкости из трубки малого радиуса силы поверхностного натяжения не позволяют жидкости выливаться сразу. При этом образуется капля жидкости (рис.2). Силой, удерживающей каплю на конце трубки, является сила поверхностного натяжения, которая может быть определена по формуле:
где r − радиус шейки капли. Отрыв капли происходит в тот момент, когда вес капли
Откуда
где m − масса оторвавшейся капли. За радиус сужения r можно приблизительно взять внутренний радиус трубки, из которой вытекает капля. В пузырьках воздуха
Экспериментальная установка изображена на рис.3. Она состоит из аспиратора (А), соединенного с манометром (М) и сосудом (В), в котором находится исследуемая жидкость. В аспиратор наливается вода. С помощью крана (К) аспиратор может отсоединяться от сосуда (В). Сосуд (В) плотно закрывается резиновой трубкой, имеющей отверстие, в которое вставляется В начальный момент времени, когда давление воздуха над поверхностью жидкости в сосуде (В) и капилляре одинаково и равно атмосферному, уровень смачивающей жидкости в капилляре выше, чем в сосуде (В), а уровень несмачивающей − ниже. Это связано с тем, что смачивающая жидкость в капилляре образует вогнутый мениск, а несмачивающая − выпуклый. Молекулярное давление под выпуклой поверхностью жидкости больше, а под вогнутой − меньше, чем молекулярное давление под плоской поверхностью. Молекулярное давление, обусловленное кривизной поверхности, принято называть избыточным (капиллярным) давлением. Избыточное давление под выпуклой поверхностью положительно, а под вогнутой − отрицательно. Оно всегда направлено к центру кривизны сечения поверхности, то есть в сторону ее вогнутости. В случае сферической поверхности избыточное давление можно вычислить по формуле:
где Высоту
где − плотность исследуемой жидкости, g − ускорение свободного падения, r − радиус кривизны мениска:
Если, повернув кран аспиратора, медленно выпускать из него воду, то
где Р − давление воздуха в сосуде (В), h − глубина погружения капилляра в жидкость,
С этого момента начинает меняться кривизна мениска, так как давление воздуха в аспираторе и сосуде (В) продолжает уменьшаться. В результате увеличения разности давлений Р радиус кривизны мениска убывает, а кривизна возрастает. Наступает момент, когда радиус кривизны становится равным внутреннему радиусу капилляра (рис.4,в), а разность давлений Р будет наибольшей. Затем радиус кривизны мениска снова увеличивается и равновесие становится неустойчивым, образуется пузырек воздуха, который отрывается от капилляра и поднимается на поверхность. Как только пузырек оторвется, жидкость затягивает отверстие и все начинается сначала. На рис.5 показано как меняется радиус кривизны мениска жидкости начиная с момента, когда он дошел до нижнего конца капилляра. Из сказанного выше следует, что:
где R − внутренний радиус капилляра. Эту разность давлений можно определить с помощью манометра, так как:
где
Так как глубина погружения капилляра в жидкость ничтожно мала
или
Таким образом, измерив экспериментально величины Порядок выполнения работы Метод отрыва кольца
1. Измерить штангенциркулем внешний диаметр кольца и микрометром его толщину. Измерения провести не менее 5 раз. При окончательных расчетах взять среднее значение 2. Промыть кольцо и внутреннюю поверхность сосуда (3) спиртом. Дать возможность им просохнуть. Ни в коем случае не прикасаться к кольцу и внутренней поверхности сосуда (3) руками. 3. Наполнить сосуд (3) водой. С помощью подвижного кронштейна (6), добиться того, чтобы нижний обрез кольца коснулся воды всеми краями одновременно. 4. Открыть кран сосуда (3), при этом уровень жидкости будет снижаться, увлекая за собой кольцо. Зафиксировать удлинение пружины, при котором кольцо оторвется от поверхности жидкости. 5. Опыт проделать 5 раз. Результаты измерений занести в таблицу 1. 6. Рассчитать коэффициент поверхностного натяжения и оценить его погрешность измерения. Таблица 1
Метод отрыва капель
1. С помощью весов определить массу 2. Закрепить (по указанию преподавателя) полиэтиленовую трубку с известным радиусом. 3. При закрытом кране (2) наполнить сосуд (1) исследуемой жидкостью. 4. Приоткрыть кран настолько, чтобы жидкость вытекала каплями. 5. Подставить взвешенный стаканчик под трубку и отсчитать 50-80 капель (по указанию преподавателя). 6. Взвесить стаканчик с жидкостью и определить массу одной капли: 7. По формуле (4) рассчитать коэффициент поверхностного натяжения жидкости. 8. Проделать опыт еще 4 раза с другим количеством капель n. Оценить погрешность измерения коэффициента поверхностного натяжения. Результаты измерений занести в таблицу 2. Таблица 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.157 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
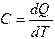 ,
, ,
, − масса моля вещества, из которого состоит тело;
− масса моля вещества, из которого состоит тело; 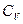 − молярная теплоемкость при постоянном объеме.
− молярная теплоемкость при постоянном объеме.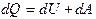
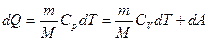 ,
,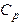 − молярная теплоемкость при постоянном давлении.
− молярная теплоемкость при постоянном давлении. , т.е.:
, т.е.: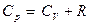 . (1)
. (1) 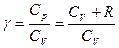 . (2)
. (2) 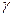 и значение изобарической теплоемкости, которое довольно легко измеряется опытным путем:
и значение изобарической теплоемкости, которое довольно легко измеряется опытным путем: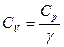
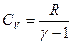 . (3)
. (3) 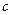 , плотность газа
, плотность газа 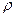 и давление
и давление 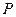 связаны между собой соотношением:
связаны между собой соотношением: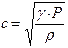 . (11)
. (11)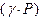 играет роль модуля объемной упругости газа. Это соотношение может быть получено из известной формулы, определяющей скорость распространения звука в твердом теле:
играет роль модуля объемной упругости газа. Это соотношение может быть получено из известной формулы, определяющей скорость распространения звука в твердом теле: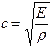 , (12)
, (12)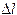 пропорционально изменению напряжения P:
пропорционально изменению напряжения P: 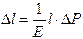 .
.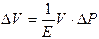 ,
,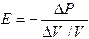 . (13)
. (13)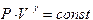 . (14)
. (14) 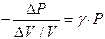 . (15)
. (15)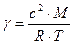 , (16)
, (16)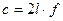 , (17)
, (17)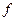 − частота звуковых колебаний.
− частота звуковых колебаний.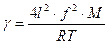 . (18)
. (18)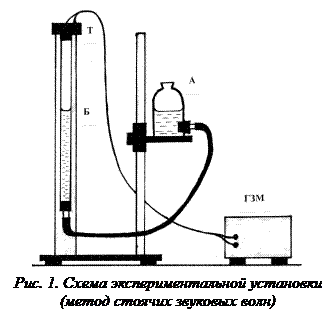 Экспериментальная установка, позволяющая определить величину
Экспериментальная установка, позволяющая определить величину 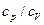 методом стоячих звуковых волн, представляет собой систему сообщающихся сосудов А и Б (рис.2). В верхней части сосуда Б расположен телефон Т (мембрана обращена внутрь трубки), который соединяется со звуковым генератором ГЗМ. Стетоскоп С, соединенный с сосудом Б, служит для определения на слух максимального звучания воздушного столба в трубке Б (резонанса), что позволяет найти l.
методом стоячих звуковых волн, представляет собой систему сообщающихся сосудов А и Б (рис.2). В верхней части сосуда Б расположен телефон Т (мембрана обращена внутрь трубки), который соединяется со звуковым генератором ГЗМ. Стетоскоп С, соединенный с сосудом Б, служит для определения на слух максимального звучания воздушного столба в трубке Б (резонанса), что позволяет найти l.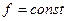 (по заданию преподавателя).
(по заданию преподавателя).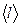 .
.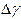 и относительную
и относительную 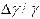 ошибки измерений. Результаты измерений и расчетов занести в таблицу 2.
ошибки измерений. Результаты измерений и расчетов занести в таблицу 2.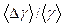 ,%
,%
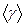 =
=
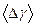 =
=
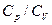 для двухатомных газов согласно молекулярно-кинетической теории теплоемкости газов?
для двухатомных газов согласно молекулярно-кинетической теории теплоемкости газов?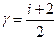 .
.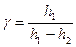 и
и 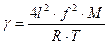 .
.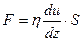 ,
, − градиент скорости.
− градиент скорости.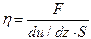 ,
,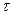 , в течение которого из баллона вытекает в мерный стакан вода объемом v = 500 см
, в течение которого из баллона вытекает в мерный стакан вода объемом v = 500 см  (объем воздуха, прошедшего через капилляр).
(объем воздуха, прошедшего через капилляр). ) (плотность манометрической жидкости взять из справочника).
) (плотность манометрической жидкости взять из справочника).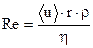 ,
,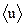 − средняя скорость течения воздуха через капилляр, r − радиус капилляра,
− средняя скорость течения воздуха через капилляр, r − радиус капилляра, 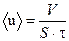 , где S − сечение капилляра. Если Re<1000, то течение ламинарное.
, где S − сечение капилляра. Если Re<1000, то течение ламинарное. , с
, с
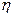 , Пас
, Пас
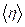 , Пас
, Пас
 , м
, м
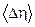 ,
Пас
,
Пас
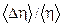 , %
, %
 Под свободной энергией понимают ту часть внутренней энергии системы, за счет которой может быть получена работа при изотермическом процессе. Величина коэффициента поверхностного натяжения жидкости определяется взаимодействием молекул жидкости и зависит от рода жидкости и ее температуры. С повышением температуры увеличиваются молекулярные расстояния и уменьшаются силы взаимодействия молекул. Поэтому коэффициент поверхностного натяжения с ростом температуры линейно уменьшается. При критической температуре он равен нулю, так как исчезает разница между жидкостью и паром, а значит и поверхность, разделяющая обе фазы.
Под свободной энергией понимают ту часть внутренней энергии системы, за счет которой может быть получена работа при изотермическом процессе. Величина коэффициента поверхностного натяжения жидкости определяется взаимодействием молекул жидкости и зависит от рода жидкости и ее температуры. С повышением температуры увеличиваются молекулярные расстояния и уменьшаются силы взаимодействия молекул. Поэтому коэффициент поверхностного натяжения с ростом температуры линейно уменьшается. При критической температуре он равен нулю, так как исчезает разница между жидкостью и паром, а значит и поверхность, разделяющая обе фазы. 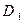 − внутренний диаметр кольца,
− внутренний диаметр кольца, 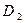 − внешний диаметр кольца, F − сила отрыва кольца от поверхности жидкости,
− внешний диаметр кольца, F − сила отрыва кольца от поверхности жидкости, 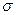 − коэффициент поверхностного натяжения. Отрыв кольца от поверхности происходит по двум окружностям. Это позволяет найти длину общей линии разрыва, а затем коэффициент поверхностного натяжения из выражения:
− коэффициент поверхностного натяжения. Отрыв кольца от поверхности происходит по двум окружностям. Это позволяет найти длину общей линии разрыва, а затем коэффициент поверхностного натяжения из выражения: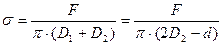 , (1)
, (1)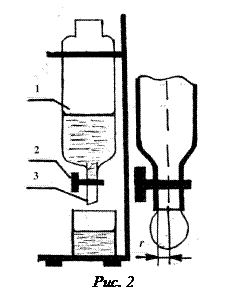
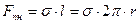 , (2)
, (2)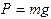 cравняется по величине с силой поверхностного натяжения.
cравняется по величине с силой поверхностного натяжения.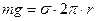 . (3)
. (3)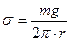 , (4)
, (4)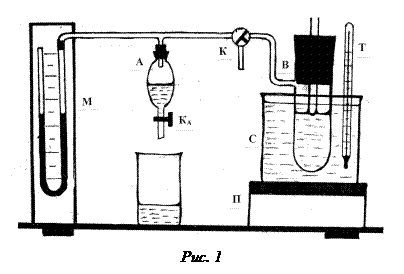 капиллярная трубка. Капилляр погружается на очень маленькую глубину в исследуемой жидкости (так, чтобы он касался поверхности жидкости). Манометр (М) измеряет разность давлений воздуха в атмосфере или, что, то же самое, в капилляре и в сосуде (В). Сосуд (В) погружен в сосуд (С) с водой, которая нагревается с помощью электроплитки (П). Контроль температуры осуществляется термометром (Т).
капиллярная трубка. Капилляр погружается на очень маленькую глубину в исследуемой жидкости (так, чтобы он касался поверхности жидкости). Манометр (М) измеряет разность давлений воздуха в атмосфере или, что, то же самое, в капилляре и в сосуде (В). Сосуд (В) погружен в сосуд (С) с водой, которая нагревается с помощью электроплитки (П). Контроль температуры осуществляется термометром (Т).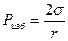 , (5)
, (5)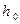 (рис.4,а) не уравновесит избыточного давления, направленного в этом случае вверх.
(рис.4,а) не уравновесит избыточного давления, направленного в этом случае вверх. 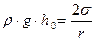 , (6)
, (6)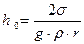 . (7)
. (7)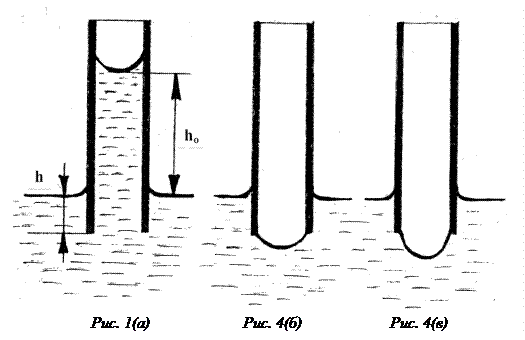 давление воздуха в аспираторе (А), в соединенных с ним сосуде (В) и колене манометра начнет уменьшаться. В капилляре же над поверхностью жидкости давление все время равно атмосферному. В результате увеличивающейся разности давлений мениск жидкости в капилляре будет опускаться, сохраняя кривизну, пока не дойдет до нижнего конца капилляра (рис.4,б). В этот момент давление воздуха в капилляре и сосуде (В) равно:
давление воздуха в аспираторе (А), в соединенных с ним сосуде (В) и колене манометра начнет уменьшаться. В капилляре же над поверхностью жидкости давление все время равно атмосферному. В результате увеличивающейся разности давлений мениск жидкости в капилляре будет опускаться, сохраняя кривизну, пока не дойдет до нижнего конца капилляра (рис.4,б). В этот момент давление воздуха в капилляре и сосуде (В) равно: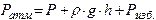 , (8)
, (8)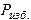 − избыточное давление, обусловленное кривизной поверхности мениска. Разность давлений воздуха в капилляре и сосуде (В) равны:
− избыточное давление, обусловленное кривизной поверхности мениска. Разность давлений воздуха в капилляре и сосуде (В) равны: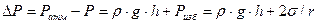 . (9)
. (9)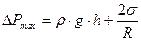 , (10)
, (10)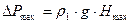 , (11)
, (11)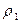 − плотность манометрической жидкости,
− плотность манометрической жидкости, 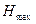 − максимальная разность уровней в коленах манометра. Из формул (10) и (11) получим:
− максимальная разность уровней в коленах манометра. Из формул (10) и (11) получим: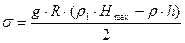 . (12)
. (12)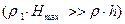 , то ею можно пренебречь и тогда:
, то ею можно пренебречь и тогда: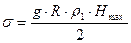 , (13)
, (13)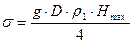 , (14)
, (14)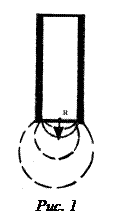 где D − внутренний диаметр капилляра (D = 1,1 мм). В том случае, когда жидкость не смачивает стенки капилляра, D в формуле (14) означает внешний диаметр капилляра.
где D − внутренний диаметр капилляра (D = 1,1 мм). В том случае, когда жидкость не смачивает стенки капилляра, D в формуле (14) означает внешний диаметр капилляра.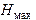 , D и,зная
, D и,зная 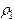 , можно вычислить коэффициент поверхностного натяжения для смачивающей и несмачивающей жидкостей. В качестве манометрической жидкости используется вода (
, можно вычислить коэффициент поверхностного натяжения для смачивающей и несмачивающей жидкостей. В качестве манометрической жидкости используется вода (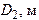
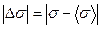 ,Н/м
,Н/м
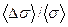 , %
, %

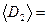
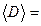
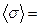
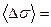
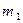 пустого стаканчика.
пустого стаканчика.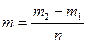 , где
, где 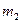 – масса стаканчика с жидкостью, n – количество капель в стаканчике.
– масса стаканчика с жидкостью, n – количество капель в стаканчике.


