
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение размеров молекул олеиновой кислотыСодержание книги
Поиск на нашем сайте
Цель работы: определение геометрических размеров молекулы олеиновой кислоты методом, основанным на явлении полного смачивания. Краткая теория
В отличие от газа или пара, которые всегда целиком заполняют предоставленный им объем, жидкости образуют свободную поверхность, отделяющую данную жидкость от пограничной среды. В поверхностном слое жидкости действуют силы поверхностного натяжения. Под действием сил поверхностного натяжения свободная поверхность жидкости стремится стать сферической. Обычно этому препятствует сила тяжести. Вследствие действия силы тяжести жидкость принимает форму того сосуда, в котором она находится, а свободная поверхность ее делается горизонтальной. Однако, в тех случаях, когда силы поверхностного натяжения значительно превосходят силу тяжести, свободная поверхность жидкости приближается к сферической (шаровидность мелких капель жидкости, сферическая форма мениска в капиллярах). Рассмотрим каплю некоторой жидкости I, расположенную на поверхности другой, не смешивающейся с ней жидкости II (рис.1).
На каждую единицу длины контура пограничной окружности будут действовать три силы поверхностного натяжения или Отсюда следует, что в случае равновесия Если же Многие органические жидкости (эфир, скипидар, керосин) растекаются на поверхности воды. Для некоторых жидкостей (бензол, жирные кислоты, масло) явление растекания наблюдается только для первых капель, помещенных на поверхности чистой воды. Последующие капли уже не растекаются, а остаются на поверхности воды в виде устойчивых капель. Это объясняется тем, что первые капли, растекаясь, загрязняют поверхность и уменьшают поверхностное натяжение настолько, что равновесие капель становится возможным.
Молекулу жирных кислот можно рассматривать как образование, сильно вытянутое в длину, нечто вроде удлиненного эллипсоида или цилиндра. Расположение таких молекул на поверхности воды показано на рис.2. Теория метода
В данной работе для определения размеров молекул олеиновой кислоты используется метод, предложенный Ленгмюром и Дево. Для измерений используется пипетка и круглая кювета (d = 0,3 м). Если капля раствора олеиновой кислоты в легколетучей жидкости падает на поверхность воды, то растворитель быстро испаряется, а олеиновая кислота, растекаясь, образует на поверхности воды мономолекулярный слой (при достаточной для этого поверхности). Если поверхность воды посыпать предварительно легким слоем пробковых опилок или талька, то на ней образуется ясно видное, свободное от порошка круглое пятно. Это дает возможность по диаметру круга приближенно рассчитать площадь поперечного сечения одной молекулы олеиновой кислоты. Если в капле содержится n молекул олеиновой кислоты с поперечным сечением
где Отсюда
Число молекул в капле можно найти, если известна масса олеиновой кислоты, содержащейся в капле и ее молярная масса М:
где NA − число Авогадро. Тогда
Длину молекулы олеиновой кислоты грубо можно оценить, пользуясь следующими соображениями:
где V − объем мономолекулярного слоя:
где Отсюда:
Порядок выполнения работы
1. Наполнить кювету на 1/3 от высоты водой и посыпать ее успокоившуюся поверхность пробковым порошком. 2. Наполнить пипетку небольшим количеством 0,3%-ного раствора олеиновой кислоты в спирте (до метки) и с высоты 2-3 мм капнуть одну каплю раствора в центр поверхности воды в кювете. 3. После установления равновесия линейкой измерить и записать 10 значений диаметров образовавшегося круга. Найти среднее значение диаметра круга. 4. Повторить опыт еще 4 раза, тщательно промывая кювету после каждого опыта. 5. Определить путем взвешивания массы пустого стаканчика. Затем, накапав в него 20 капель раствора олеиновой кислоты из той же пипетки, определить массу стаканчика с раствором. Рассчитать массу одной капли раствора. В капле раствора будет содержаться масса олеиновой кислоты:
6. Рассчитать площадь поперечного сечения и длину молекулы олеиновой кислоты по формулам (4) и (7). Плотность олеиновой кислоты принять равной 890 кг/м 7. Оценить абсолютную и относительную погрешности измерений площади поперечного сечения и длины молекулы олеиновой кислоты. 8. Вычислить эффективный диаметр молекулы олеиновой кислоты.
Таблица 1
Контрольные вопросы
1. Каковы современные представления о структуре жидкостей? 2. Чем объясняется шарообразная форма небольших капель жидкости? 3. Объяснить процесс образования капли жидкости при выходе ее из трубки. 4. Написать условия равновесия капли жидкости, находящейся на поверхности несмешивающейся с ней другой жидкости. 5. Написать условия равновесия капли жидкости на поверхности твердого тела. 6. Что такое краевой угол? 7. Какие явления называются полным смачиванием, частичным смачиванием, частичным несмачиванием и при каких условиях они наблюдаются? 8. Что такое мениск? Каким он будет у смачивающих и несмачивающих поверхность жидкостей? 9. Почему в данной работе взвешивается не одна, а двадцать капель раствора олеиновой кислоты? 10. Почему при использовании одной кюветы нужно тщательно промывать ее перед каждым измерением диаметра круга?
Литература
1. Фриш, С.Э. Курс общей физики: учебник: [в 3 т.]. Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны / С.Э. Фриш. – 13-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2009. – 480 с.: ил. 2. Савельев, И.В. Курс общей физики: учебное пособие для вузов [в 3 т.]. Т. 1. Механика. Молекулярная физика / И.В. Савельев. – 10-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2008. – 432 с.: ил. 3. Трофимова, Т.И. Основы физики: учебное пособие: в 5 кн. Кн.2. Молекулярная физика. Термодинамика / Т.И. Трофимова. – Москва: Высшая школа, 2007. – 180 с.: ил. 4. Пронин, Б.В. Физика [Электронный ресурс]: учебник / Б.В. Пронин. – Москва: Издательство РГАУ-МСХА имени К.А. Тимирязева, 2012. – 445 с. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=144822
ЛАБОРАТОРНАЯ РАБОТА № 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 925; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.85 (0.011 с.) |

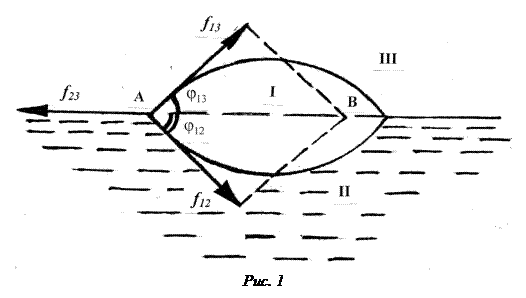 Форма капли устанавливается в данном случае под влиянием взаимодействия трех сред: жидкости I, жидкости II и воздуха III. Эти три среды имеют общую границу – окружность, ограничивающую каплю и пересекающую плоскость чертежа в двух точках А и В. По этой окружности пересекаются между собой три поверхности, поверхность, разграничивающая жидкость II и воздух, с коэффициентом поверхностного натяжения
Форма капли устанавливается в данном случае под влиянием взаимодействия трех сред: жидкости I, жидкости II и воздуха III. Эти три среды имеют общую границу – окружность, ограничивающую каплю и пересекающую плоскость чертежа в двух точках А и В. По этой окружности пересекаются между собой три поверхности, поверхность, разграничивающая жидкость II и воздух, с коэффициентом поверхностного натяжения 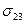 ; поверхность, разграничивающая жидкость I и воздух, с коэффициентом поверхностного натяжения
; поверхность, разграничивающая жидкость I и воздух, с коэффициентом поверхностного натяжения 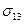 ; поверхность, разграничивающая жидкости I и II, с коэффициентом поверхностного натяжения
; поверхность, разграничивающая жидкости I и II, с коэффициентом поверхностного натяжения  .
. ,
, 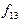 и
и 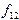 . Эти силы будут направлены перпендикулярно к отдельным элементам контура окружности и по касательным к соответствующим поверхностям раздела. В случае, когда можно пренебречь силой тяжести, по сравнению с силами поверхностного натяжения, равновесной будет та форма капли, при которой:
. Эти силы будут направлены перпендикулярно к отдельным элементам контура окружности и по касательным к соответствующим поверхностям раздела. В случае, когда можно пренебречь силой тяжести, по сравнению с силами поверхностного натяжения, равновесной будет та форма капли, при которой: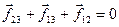
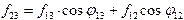 .
.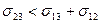 , так как
, так как 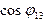 и
и  меньше единицы.
меньше единицы.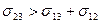 , то равновесие капли жидкости I на поверхности жидкости II невозможно, и поэтому капля растекается по поверхности тонким молекулярным слоем.
, то равновесие капли жидкости I на поверхности жидкости II невозможно, и поэтому капля растекается по поверхности тонким молекулярным слоем.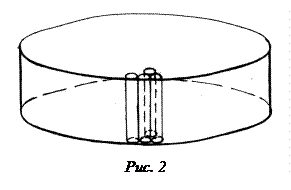 Многочисленные эксперименты, в частности опыты Ленгмюра, Дево, Релея и других, привели к выводу, что если площадь поверхности воды достаточно велика, то капля масла (например, касторового) или жирных кислот, соответствующего объема растекается в очень тонкий мономолекулярный слой. Произведенные вычисления показали, что площадь
Многочисленные эксперименты, в частности опыты Ленгмюра, Дево, Релея и других, привели к выводу, что если площадь поверхности воды достаточно велика, то капля масла (например, касторового) или жирных кислот, соответствующего объема растекается в очень тонкий мономолекулярный слой. Произведенные вычисления показали, что площадь  , занимаемая каждой молекулой, очень мала. Для жирных кислот
, занимаемая каждой молекулой, очень мала. Для жирных кислот 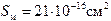 .
.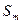 , то
, то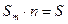 , (1)
, (1)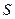 − площадь полученного круга.
− площадь полученного круга.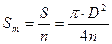 . (2)
. (2) , (3)
, (3)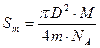 . (4)
. (4)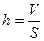 , (5)
, (5) , (6)
, (6)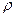 − плотность олеиновой кислоты.
− плотность олеиновой кислоты.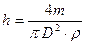 . (7)
. (7)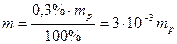 . (8)
. (8) . Молярную массу рассчитать по химической формуле олеиновой кислоты. Результаты измерений и расчетов занести в таблицу 1.
. Молярную массу рассчитать по химической формуле олеиновой кислоты. Результаты измерений и расчетов занести в таблицу 1. м
м
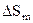 ,м2
,м2
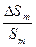 ,%
,%
 м
м
 ,%
,%



