
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные ошибки. Ошибки разбросаСодержание книги
Поиск на нашем сайте
По результатам многократных наблюдений определяются наилучшие значения измеряемой величины и оценивается погрешность измерения. Если проведено п наблюдений величины х и получен ряд значений х изм.= х1,х2, …, хп то ошибки + В этом случае используется правило: при отсутствии информации о причинах наблюдаемого разброса за наиболее вероятное значение измеряемой величины следует принять среднее арифметическое измеряемых значений: В большинстве случаев x 0 является лучшей оценкой истинного значения x, чем любое из значений x изм. Это единственное правило, принятое без всяких гипотез о данном конкретном эксперименте. При выполнении гипотезы о том, что эксперимент «проведен хорошо», за ошибку, которую мы можем совершить, принимая для x 0 по порядку величины не больше ширины разброса, будет:
В простейшей методике обработки измерений величину r и принимают в качестве меры точности. Её называют абсолютной погрешностью по разбросу Средняя квадратичная ошибка входит в закон Гаусса: где Средние ошибки складываются, также складываются и дисперсии независимых слагаемых:
Истинное значение измеряемой величины х, полученное в результате измерений х0 при погрешности этой величины x о- Пусть Последнее выражение означает, что с вероятностью, равной Для нахождения случайной ошибки, таким образом, определяются два числа – величина ошибки (погрешности) и доверительная вероятность. Средней квадратичной ошибке При оценке погрешности непосредственного измерения встречаются следующие возможные ошибки: 1. Ошибки разброса. 2. Ошибки отсчитывания. 3. Инструментальные ошибки (ошибки градуировки).
Ошибки разброса В них проявляются ошибки наводки, ошибки, связанные с нестабильностью или неопределенностью измеряемой величины или условий эксперимента и т.п. Единственным способом уменьшения или оценки ошибок разброса являются многократные наблюдения. Вычисляется по формуле (2):
Ошибки отсчитывания Ошибки отсчитывания
В учебной лаборатории считается обязательным отсчитывать все показания приборов с максимально возможной точностью и указывать достигнутую точность. Эту величину нельзя определить заранее для всех измерений. Её следует фиксировать при каждом отсчете. В большинстве случаев допускаемая инструментальная погрешность лежит в интервале от 0,5 d до 1 d.
Ошибки градуировки
Эти ошибки связаны с неточностью градуировки, не проявляются в разбросе, если измерения выполнены на одних и тех же приборах. Их возможная величина, характеризуемая предельной допускаемой погрешностью градуировки Полная погрешность непосредственного измерения складывается из вышеперечисленных составляющих – ошибки отсчитывания
Если одна из складываемых величин больше, чем в 3 раза превышает каждую из двух других, то ими можно пренебречь и положить При выполнении и обработке результатов прямых измерений следует руководствоваться следующими правилами: 1. Проводится не менее 4-5 наблюдений и их результаты х i (i = 1, 2,…, n) записываются вместе с погрешностью отсчитывания и градуировки: 2. Вычисляется наиболее вероятное значение величины: 3. Погрешность по разбросу вычисляется как где 4. Вычисляется полная погрешность по формуле: 5. Записывается окончательный результат: Если необходимо, к значению
Относительная погрешность Средней относительной погрешностью измерений называется отношение средней абсолютной погрешности к среднему значению измеряемой величины. Относительная ошибка является величиной безразмерной и выражается обычно в процентах:
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.225 (0.008 с.) |

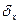 и -
и - 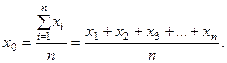 (1)
(1)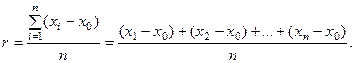 (2)
(2)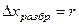 . Термин «абсолютная» отражает метод усреднения. Помимо средней арифметической ошибки используется и средняя квадратичная ошибка
. Термин «абсолютная» отражает метод усреднения. Помимо средней арифметической ошибки используется и средняя квадратичная ошибка 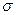 :
: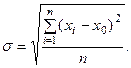 (3)
(3)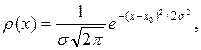 (4)
(4)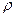 (x) – вероятность появления погрешности величины х; е = 2, 71…,
(x) – вероятность появления погрешности величины х; е = 2, 71…, 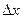 . Для распределения Гаусса r = 0,8
. Для распределения Гаусса r = 0,8 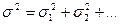
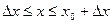 .
.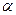 означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем
означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем 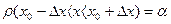 . (5)
. (5)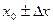 .
. 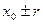 равна 75 – 80 % или выше. При непосредственных измерениях значение интересующей нас величины получается непосредственно из отсчета по прибору. При косвенных измерениях оно вычисляется как функция одной или нескольких вычисляемых величин.
равна 75 – 80 % или выше. При непосредственных измерениях значение интересующей нас величины получается непосредственно из отсчета по прибору. При косвенных измерениях оно вычисляется как функция одной или нескольких вычисляемых величин.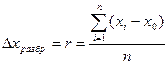 .
.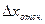 оцениваются наблюдателем субъективно. Необходимо, чтобы доверительная вероятность такой оценки была около 80%. Ошибка отсчитывания характеризуется предельной погрешностью отсчитывания. Если цена деления прибора или измерительного инструмента равна d, то наблюдатель может указать:
оцениваются наблюдателем субъективно. Необходимо, чтобы доверительная вероятность такой оценки была около 80%. Ошибка отсчитывания характеризуется предельной погрешностью отсчитывания. Если цена деления прибора или измерительного инструмента равна d, то наблюдатель может указать: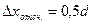 - при округлении до целых делений,
- при округлении до целых делений,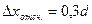 - при отсчете целых делений и половины,
- при отсчете целых делений и половины,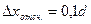 - при отсчете десятых долей деления.
- при отсчете десятых долей деления.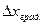 , указываются на шкале прибора или в паспорте. Если этого нет, то она отсчитывается равной цене деления шкалы прибора. Доверительная вероятность
, указываются на шкале прибора или в паспорте. Если этого нет, то она отсчитывается равной цене деления шкалы прибора. Доверительная вероятность 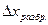 :
: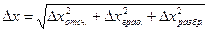 (6)
(6)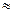 75 – 80 %.
75 – 80 %.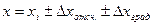
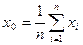 .
.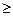 4,
4,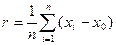 .
.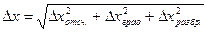
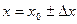 .
.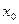 добавляется поправка, учитывающая, например, изменение величины с изменением температуры, т.е.
добавляется поправка, учитывающая, например, изменение величины с изменением температуры, т.е.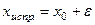 (
(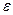 - поправка) и тогда
- поправка) и тогда 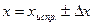 .
.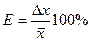 . (7)
. (7)


