
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория метода и экспериментальная установкаДля определения динамической вязкости воздуха воспользуемся методом истечения воздуха через капилляр. Экспериментальная установка изображена на рисунке 1. Один конец капилляра К, через который протекает воздух, соединяется тройником 1 с левым коленом манометра М. Другой конец Если открыть кран В, то вследствие вытекания воды давление в баллоне будет уменьшаться и в него будет засасываться воздух, который пройдет через капилляр К. Скорости движения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, будут различны. В случае если установившееся течение является ламинарным (слоистым), скорости по сечению капилляра распределяются по параболическому закону. Если считать, что для слоя, прилегающего к стенкам капилляра, имеет место явление «прилипания», то скорость этого слоя равна нулю. Наибольшая скорость будет по осевой линии капилляра. Вследствие различия скоростей слоев между ними возникнут силы внутреннего трения. При установившемся движении сила вязкости, действующая на элементарный цилиндрический объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давления, действующих на основание цилиндра. На концах капилляра, при протекании через него воздуха, будет существовать разность давлений (давление на входе будет больше давления на выходе). При установившемся давлении воздуха разность давлений будет неизменной, так как в этом случае параметры, характеризующие течение (скорость, давление в различных точках потока), не меняются с течением времени и являются функцией только координат. Для случая установившегося ламинарного течения вязкой, но несжимаемой жидкости по капилляру радиусом r справедлива формула Гагена-Пуазейля:
где V − объем жидкости, протекающей через сечение капилляра за единицу времени, ( Так как в отличие от жидкостей, практически несжимаемых, газы обладают значительной сжимаемостью и поэтому закон Гагена-Пуазейля в такой форме записи, строго говоря, к газам неприменим. Лишь при малых разностях давлений, когда ( При больших перепадах давления, вследствие значительной сжимаемости газов, разность давлений, приходящихся на единицу длины капилляра, не будет постоянной, т.е. вдоль оси капилляра будет меняться градиент давления. Поэтому при этих условиях формулу (1) можно применить только к бесконечно малому участку длины капилляра. В данной работе измерения производятся при небольших разностях давлений на концах капилляра и поэтому для расчетов может быть использована эта формула. Объем воздуха, протекающего через сечение капилляра за время, будет равен:
Зная значение r = 0,525 мм, ( При точных расчетах динамической вязкости необходимо ввести поправку на скольжение молекул газа по внутренней поверхности капилляра (при течении газа нельзя говорить о «прилипании» к стенкам капилляра слоя газа, прилежащего к ним). В данной работе этой поправкой можно пренебречь. Из молекулярно-кинетической теории вытекает формула, связывающая вязкость газа со средней длиной свободного пробега молекул:
где
Средняя скорость газовых молекул может быть найдена из распределения Максвелла:
Плотность газа можно найти из уравнения Менделеева-Клапейрона:
Подставляя (3), (6), (7) в формулу (5), получим:
Эффективный диаметр молекулы можно найти из соотношения связи его со средней длиной свободного пробега:
где
Тогда:
Порядок выполнения работы
1. При закрытом кране В, наполнить баллон водой на 3/4 объема. 2. Открыть кран В и отрегулировать скорость истечения воды таким образом, чтобы разность уровней жидкости в коленах манометра не превышала 2-3 см. 3. Убедившись в том, что течение воздуха через капилляр установилось (в этом случае h остается неизменной), измерить h и с помощью секундомера определить время 4. Не изменяя разность уровней, измерить еще два раза время, в течение которого из баллона вытекает вода объемом v = 500 см 5. Изменив разность уровней, провести измерения, согласно п.3 и п.4, не менее 3 раз. 6. Вычислить значение динамической вязкости, средней длины свободного пробега, эффективного диаметра, среднюю абсолютную и среднюю относительную ошибки измерений. Результаты опытов и расчетов занести в таблицу 1. 7. Для того, чтобы установить было ли течение воздуха ламинарным, вычислить число Рейнольдса: где Средняя скорость: Замечание: если время вытекания одного и того же объема воды определяется при несколько отличающихся разностях давлений, усреднить это время нельзя. В этом случае динамическая вязкость рассчитывается три раза, а затем находится ее среднее значение. Таблица 1
Продолжение таблицы 1
Контрольные вопросы
1. Что называется эффективным диаметром газовых молекул? 2. Как зависит эффективный диаметр от температуры и давления? 3. Что называется длиной свободного пробега газовых молекул? 4. Как зависит длина свободного пробега от температуры и давления? 5. Что называется вязкостью газов, и от каких параметров она зависит? 6. Как объяснить различие температурной зависимости динамической вязкости газов и жидкостей? 7. Получить выражение для определения динамической вязкости газов методом истечения через капилляр? 8. Какие другие методы применяются для определения динамической вязкости жидкостей и газов? 9. Что называется кинематической вязкостью, и в каких единицах она измеряется? 10. Какое течение называется ламинарным? 11. Какой физический смысл имеет число Рейнольдса?
Литература
1. Фриш, С.Э. Курс общей физики: учебник: [в 3 т.]. Т. 1. Физические основы механики. Молекулярная физика. Колебания и волны / С.Э. Фриш. – 13-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2009. – 480 с.: ил. 2. Савельев, И.В. Курс общей физики: учебное пособие для вузов [в 3 т.]. Т. 1. Механика. Молекулярная физика / И.В. Савельев. – 10-е изд., стер. – Санкт-Петербург [и др.]: Лань, 2008. – 432 с.: ил. 3. Трофимова, Т.И. Основы физики: учебное пособие: в 5 кн. Кн.2. Молекулярная физика. Термодинамика / Т.И. Трофимова. – Москва: Высшая школа, 2007. – 180 с.: ил. 4. Пронин, Б.В. Физика [Электронный ресурс]: учебник / Б.В. Пронин. – Москва: Издательство РГАУ-МСХА имени К.А. Тимирязева, 2012. – 445 с. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=144822
ЛАБОРАТОРНАЯ РАБОТА № 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.61.119 (0.005 с.) |
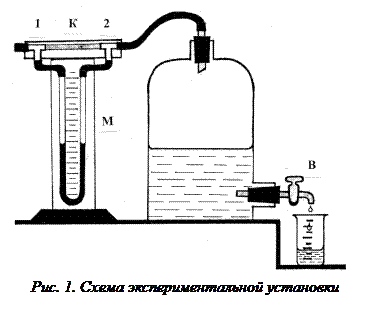 капилляра с помощью тройника 2 соединяется со стеклянным баллоном и правым коленом манометра М.
капилляра с помощью тройника 2 соединяется со стеклянным баллоном и правым коленом манометра М.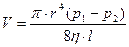 , (1)
, (1)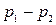 ) − разность давлений в начале и в конце капилляра, l − длина капилляра.
) − разность давлений в начале и в конце капилляра, l − длина капилляра.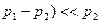 (и, соответственно, малых скоростях течения газов), сжимаемостью газов можно пренебречь и применить к ним формулу Гагена-Пуазейля.
(и, соответственно, малых скоростях течения газов), сжимаемостью газов можно пренебречь и применить к ним формулу Гагена-Пуазейля.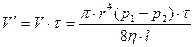 . (2)
. (2)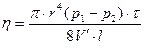 . (3)
. (3)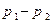 ),
), 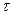 ,
,  и l = 15,1 см, можно определить динамическую вязкость воздуха.
и l = 15,1 см, можно определить динамическую вязкость воздуха.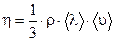 (4)
(4) − средняя длина свободного пробега,
− средняя длина свободного пробега,  − средняя арифметическая скорость молекул, т.е. среднее значение абсолютной величины скорости молекул. Из формулы (4) получаем:
− средняя арифметическая скорость молекул, т.е. среднее значение абсолютной величины скорости молекул. Из формулы (4) получаем: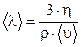 . (5)
. (5)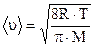 . (6)
. (6)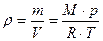 . (7)
. (7)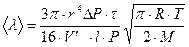 . (8)
. (8)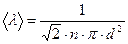 , (9)
, (9)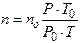 − число молекул в единице объема при данных условиях;
− число молекул в единице объема при данных условиях;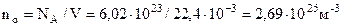 − число Лошмидта (число молекул в единице объема при нормальных условиях).
− число Лошмидта (число молекул в единице объема при нормальных условиях). . (10)
. (10) (объем воздуха, прошедшего через капилляр).
(объем воздуха, прошедшего через капилляр). ) (плотность манометрической жидкости взять из справочника).
) (плотность манометрической жидкости взять из справочника).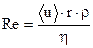 ,
,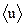 − средняя скорость течения воздуха через капилляр, r − радиус капилляра,
− средняя скорость течения воздуха через капилляр, r − радиус капилляра, 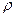 − плотность воздуха при комнатной температуре и атмосферном давлении (из справочника).
− плотность воздуха при комнатной температуре и атмосферном давлении (из справочника).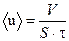 , где S − сечение капилляра. Если Re<1000, то течение ламинарное.
, где S − сечение капилляра. Если Re<1000, то течение ламинарное. , с
, с
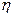 , Пас
, Пас
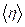 , Пас
, Пас
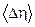 ,
Пас
,
Пас
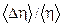 , %
, %



