Способы решения текстовых задач в начальном курсе математики

Всякая хорошо решённая математическая задача доставляет умственное наслаждение, а сосредоточенные размышления успокаивают сердце, делая его созвучным Вселенной.

                                                  Г. Гессе [21].

Федеральный государственный образовательный стандарт начального общего образования ориентирует учителей начальных классов на формирование общего приёма обучения решению задач.

Как отмечает Н.Б. Истомина, «понятие «решение задачи» можно рассматривать с различных точек зрения: решение как результат, т.е. ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата. С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который, в свою очередь, тоже можно рассматривать с различных точек зрения. Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, которые входят в тот или иной способ» [10].

Рассмотрим различные способы решения текстовых задач. Традиционно в методике преподавания математики используют два основных способа решения задач: арифметический и алгебраический. Реже используют практический и графический способы решения задач.

Арифметический способ решения задач является одним из главных в начальном курсе математики. При решении задачи арифметическим способом ответ на вопрос находится в результате выполнения арифметических действий над числами. Решение задачи с помощью указанного способа оформляется в виде последовательности числовых равенств, к которым даются пояснения, или в виде числового выражения.

Возможно решение задачи различными арифметическими способами: речь идёт о возможности установления различных связей между данными и искомыми, а, следовательно, о выборе других действий и другой их последовательности для ответа на вопрос задачи.

Прочное усвоение решения задач арифметическим способом позволяет подготовить учащихся к осознанному решению задач алгебраическим способом.

Алгебраический способ основан на использовании уравнений при решении задачи. Американский педагог и математик Д. Пойа в книге по проблемам обучения решению задач писал, что «…составить уравнение – значит выразить математическими символами условие, сформулированное словами…»[15]. В зависимости от выбора неизвестного для обозначения буквой, от хода рассуждений можно составить различные уравнения по одной и той же задаче. В этом случае можно говорить о различных алгебраических решениях этой задачи. В начальной школе за неизвестное число в уравнении принимается то число, о котором спрашивается в задаче, и, установив взаимосвязи между данными и искомым, составляется уравнение. Решают уравнения младшие школьники методом установления взаимосвязи между компонентами и результатами действий или через установление взаимосвязи между частью и целым.

Некоторые авторы учебников включают в учебные пособия задания, требующие применения обоих способов решения задачи. Приведём пример из учебника для 4 класса И.И. Аргинской, Е.И. Ивановской, С.Н. Кормишиной [3, С.68].

 

             

 

 

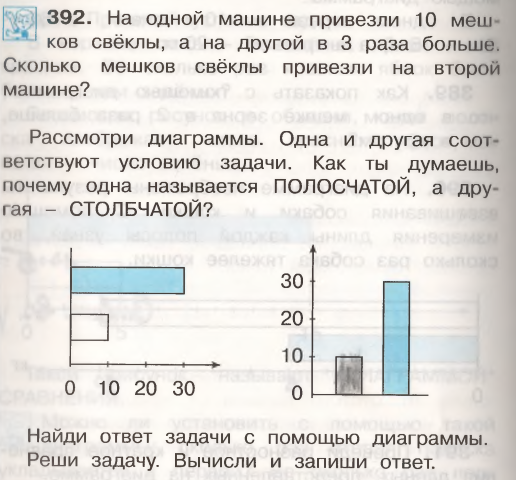
Практический способ решения задачи предусматривает интерпретацию действий с предметами или с их изображениями, и также как и графический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

Практический способ решения задач важен при знакомстве младших школьников с конкретным смыслом арифметических действий.

Графический способ решения задачи представляет собой получение результата с помощью применения отрезков или диаграммы, используя счёт и присчитывание, не выполняя арифметических действий. Н.Б. Истомина считает, что графический способ близок к практическому, но имеет более абстрактный характер и требует специальной подготовки учащихся[10].

Представим задание из учебника для 3 класса А.Л. Чекина, иллюстрирующего графический способ решения задачи с помощью диаграмм [23,С.114].

 

ы.

 

Приведём пример из практики. Покажем решение одной и той же задачи различными способами:

 

Практический способ

Обозначим каждую собаку кругом. Изобразим 9 кругов и обозначим окраску собак: «б» – белые, «ч» – чёрные

б

ч

ч

ч

б

                                                                                                                

 

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество рыжих собак соответствует тем кругам, которые не обозначены.

 Арифметический способ (I)

1) 2 + 3 = 5 (с.) – белые и чёрные

2) 9 – 5 = 4 (с.) – рыжие собаки

    Арифметический способ (II)

1) 9 – 2 = 7 (c.) – черные и рыжие

2) 4 – 3 = 2 (с.) – рыжие собаки

Алгебраический способ

Пусть x – количество рыжих собак. Тогда количество всех собак можно обозначить с помощью выражения: 2 + 3 + x. По условию задачи известно, что всего на прогулку вывели 9 собак. Значит, 2 + 3 + x = 9.

Решив данное уравнение, мы ответим на вопрос задачи.

    Графический способ

белые черные           рыжие

 

 

Графический способ решения задачи также как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.