
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика организации учебно-познавательной деятельности младших школьников на уроках математикиСодержание книги
Поиск на нашем сайте
Методика организации учебно-познавательной деятельности младших школьников на уроках математики
Учебное пособие для студентов II-I V курсов очной и заочной форм обучения по направлению 44.03.01 «Педагогическое образование», профиль «Начальное образование»
ВОРОНЕЖ Воронежский государственный педагогический университет 2018
Авторы: кандидат педагогических наук, доцент Н.А. Иванова кандидат педагогических наук, доцент О.В. Бахтина
Рецензенты: доктор педагогических наук, профессор кафедры педагогики и педагогической психологии Воронежского государственного университета И.Ф. Бережная кандидатпедагогических наук, доцент кафедры общей и социальной педагогики Воронежского государственного педагогического университета Т.В.Кульневич
ПРЕДИСЛОВИЕ В настоящее время самое пристальное внимание уделяется формированию профессиональных компетенций будущих учителей начальных классов в области математики и методики её преподавания. В современной начальной школе на передний план выдвинуты задачи реализации системно-деятельностного подхода, формирования не только предметных, но и метапредметных умений учащихся. Учитывая необходимость достижения планируемых результатов в обучении младших школьников, необходимо иметь в виду и изменения в процессе подготовки будущих учителей начальных классов. Важнейшую роль при этом играет методическая подготовка студентов, реализуемая не только на занятиях, но в процессе педагогической (производственной) практики, которая интегрирует в себе специальные (математические), психолого-педагогические и методические знания, умения. При построении пособия авторы старались учесть процесс организации деятельности студентов по усвоению методических знаний и умений, а также связь методического курса с курсами математики, педагогики, психологии. Пособие поможет обучающимся, учителям начальных классов реализовать системно-деятельностный подход на практике, проектировать и организовывать деятельность учеников при изучении различных разделов математики. Представленные в пособии темы являются ключевыми в курсе методики преподавания математики. Лекционный и практический материал содержат обзор вариативных образовательных программ современной начальной школы, примеры организации деятельности учащихся по разным учебникам математики. Учебное пособие предназначено для студентов II-IV курсов очной и заочной форм обучения по направлению подготовки 44.03.01 «Педагогическое образование», профиль «Начальное образование». Кроме того, предложенный методический материал будет полезным и необходимым студентам педагогических колледжей, учителям начальной школы.
Таблица 1.1. Компоненты учебной деятельности: позиции учителя и ученика
Методические аспекты реализации системно-деятельностного подхода на уроках математики мы рассмотрим в следующем параграфе. Вопросы и задания для самостоятельной работы 1. Перечислите основные документы, лежащие в основе деятельности учителя начальных классов. 2. Каковы отличительные особенности ФГОС НОО? 3. Какова цель образования согласно Стандарту? 4. Какие требования предъявляет Стандарт к результатам освоения обучающимися основной образовательной программы начального общего образования? 5. Познакомьтесь с Примерной основной образовательной программой начального общего образования (в редакции № 3/15 от 28.10.2015). Какова структура примерной программы по математике? Перечислите основные дидактические линии, подлежащие изучению на уроках математики в начальной школе. Приведите примеры планируемых предметных результатов, обозначив уровень освоения учебного материала. 6. Раскройте содержание понятие «системно-деятельностный подход». 7. Дайте определение учебной деятельности и соотнесите ее компоненты с этапами урока в начальной школе.
Литература 1. Бахтина О.В., Иванова Н.А. Особенности Федерального государственного образовательного стандарта начального общего образования /Актуальные проблемы обучения и воспитания школьников и студентов в образовательном учреждении. Выпуск 5: сборник научных статей / [под ред. И.Ф. Бережной]; Воронежский государственный университет. – Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2011. – С. 71-76. 2. Большая психологическая энциклопедия – http://psychology.academic.ru/554 (23.02.2017) 3. Данилюк А.Я., Кондаков А.М., Тишков В.А. Концепция духовно-нравственного развития и воспитания личности гражданина России/А.Я Данилюк и др. – М.: «Просвещение», 2011. – 23 с. 4. Дозморова Е.В. Новая система оценивания образовательных результатов // Методические рекомендации по формированию содержания и организации образовательного процесса / сост. Т.В. Расташанская. – Томск: ТОИПКРО, 2010. 5. Краткий словарь философских терминов - http://nenuda.ru›краткий-словарь-философских-терминов.html (23.02.2017). 6. [Начальная школа ХХI века. - https://refdb.ru/look/1207765.html] 7. Столяр А.А. Педагогика математики. / Столяр А.А. – Минск, Вышейшая школа, 1986. – 414 с. 8. Федеральный государственный образовательный стандарт начального общего образования – http://mon.gov.ru/files/materials/7195/373.pdf 9. Э льконин Д.Б. Психологические вопросы формирования учебной деятельности в младшем школьном возрасте. – В кн.: Вопросы психологии обучения и воспитания / Под ред. Г.С. Костюка, П.Р. Чаматы. Киев, 1961. – 296 с.
Урок рефлексии Деятельностная цель: формирование у учащихся способностей к рефлексии коррекционно-контрольного типа и реализации коррекционной нормы (фиксирование собственных затруднений в деятельности, выявление их причин, построение и реализация проекта выхода из затруднения и т.д.). Образовательная цель: формирование умения применять изученные понятия, алгоритмы и т.д. Конспект урока математики (система Л.В. Занкова, учебник И.И. Аргинской, Е.П. Бененсон,1 класс, часть 2-я, 2012 г.) Тема: « Угол. Виды углов». Цели урока: познакомить с новой геометрической фигурой – углом, его образованием, с разными видами углов, способами их получения и соотношениями между ними. Деятельностная цель: формирование у учащихся умения построения и реализации новых знаний (понятий, способов действий и т.д.). Самостоятельная работа с самопроверкой по эталону При проведении данного этапа используется индивидуальная форма работы: учащиеся самостоятельно выполняют задание по новой теме, осуществляют самопроверку и сами оценивают ее. Эмоциональная направленность этапа состоит в организации ситуации успеха, способствующей включению учащихся в дальнейшую познавательную деятельность. - Применим знания в деле. Задание: начертить острый, прямой и тупой углы и обозначить их. Проверка по эталону.
А
А В С О
- Какие еще задания можно придумать на закрепление этой темы? (Дети предлагают задания: например, соотнести название угла с сами углом). Урок решения учебной задачи Учитель, сталкивая учащихся с необходимостью овладеть новыми способами действий, организует их поиск. Решить учебную задачу, значит отыскать общий способ, принцип подхода ко многим частным задачам данного типа. В начале урока учитель организует общеклассную дискуссию. Педагог включается в решение задачи наравне с учениками, погруженным в действие, задаёт логику поиска. Функция учителя – организация совместных действий детей как внутри одной группы, так и между группами. На этом этапе работы учителю важно обеспечить участие каждого ребенка в совместных действиях по удержанию и решению учебных задач. В структуре урока выделяются три компонента: 1. Анализ условий решения задачи. 2. Собственно решение задачи, конструирование нового способа действия. 3. Рефлексия. 3. Урок моделирования и преобразования модели Цель моделирования – выделить и зафиксировать наиболее общее отношение в предмете для его исследования. В развивающем обучении моделирование напрямую связано с предметными действия учащихся. Модель выполняет планирующую и контролирующую функции в деятельности учащихся. На данном этапе предполагаются абстрактные задания, когда отношения осмыслены и неоднократно отражены в знаках и схемах. Под моделированием понимают необходимость строить действие с реальными предметами, которое он уже сможет выполнить, то есть умственное действие. Урок моделирования обеспечивает: - построение модели как средства конструирования нового способа; - обучение построению модели на основе анализа принципов, способов ее создания. «Место» модели определяется в зависимости от задания. Когда способ решения задачи находится практически, модель строится по окончании действий для того, чтобы осмыслить их. Учитель может использовать вопросы: как ты это делал? Как бы ты научил других выполнять такие задания? Критерии правильности построения модели определяются по отражению в предмете и способам действия с ним. Поощряется создание детьми разных моделей. Учитель побуждает учащихся к развёрнутому анализу моделей. Прослеживание последовательности мыслей другого учащегося позволяет ребёнку проанализировать своё решение. Урок моделирования имеет следующую структуру: 1. Преобразование условия задачи. 2. Моделирование каждым учащимся. 3. Преобразование модели. 4. Рефлексия. Урок контроля и оценки Контроль является неотъемлемым звеном каждого урока. Основная цель урока контроля и оценки для учителя: через контрольно-оценочные действия детей проверить и оценить их уровень овладения известным способом действия и понимания границ его применения. Требования к задачам данного урока: - задачи решаются согласно известному способу действий (действия по плану) и способам самопроверки; - обязательными являются задания, содержащие ошибки, связанные с использованием изученного действия (поиск, обнаружение, исправление и анализ); - наличие заданий с «ловушками». Объясняя смысл «ловушек», ученики возвращаются к характеристикам понятия.
***** Какую бы типологию уроков не выбрал учитель, для того, чтобы знания учащихся были результатом их собственных поисков, необходимо организовать эти поиски, развивать их познавательную деятельность. Для построения урока в рамках ФГОС НОО важно понять, какими должны быть критерии результативности урока, вне зависимости от того, какой типологии мы придерживаемся.
Вопросы и задания для самостоятельной работы 1. Дайте характеристику технологии деятельностного метода обучения. В чем суть дидактических принципов, лежащих в его основе? 2. Раскройте структуру учебной деятельности, охарактеризуйте ее компоненты. 3. Назовите типы уроков в зависимости от их целей. Каковы их деятельностные и образовательные цели? 4. Опишите структуру урока «открытия нового знания». 5. Назовите типы уроков по А.К. Дусавицкому. Чем в этой классификации определяется тип урока? 6. Разработайте фрагмент (конспект) конспекта урока рефлексии на тему: «Порядок выполнения действий в выражениях» (3класс).
Литература 1. Афоризмы Джордж Бернард Шоу – http://www.orator.ru/shaw.html 2. Выготский Л.С. Проблема возраста // Выготский Л.С. Собрание сочинений: В 6-ти т.; Т.4. – М.: Педагогика, 1984. – 432 с. 3. Дусавицкий А.К. Урок в развивающем обучении: Книга для учителя / А.К.Дусавицкий, Е.М. Кондратюк, И.Н. Толмачева, З.И. Шилкунова. – 2-е изд. – М.: ВИТА-ПРЕСС, 2010. – 288 с. 4. Деятельностный метод обучения: описание технологии, конспекты уроков. 1-4 классы / авт.-сост. И.Н. Корбакова, Л.В. Терешина. – Волгоград: Учитель, 2008. – 118 с. 5. Петерсон Л.Г., Агапов Ю.В. Система и структура учебной деятельности в контексте современной методологии. – Л.Г. Петерсон, Ю.В. Агапов, М.А. Кубышева, В.А. Петерсон. – М.: АПКиППРО: УМЦ «Школа 2000…», 2006. – 92 с. 6. Петерсон Л.Г., Кубышева М.А. Типология уроков деятельностной направленности. – М.: АПКиППРО: УМЦ «Школа 2000…», 2008. – 48 с. 7. Петерсон Л.Г., Кубышева М.А. Что значит «уметь учиться». – Л.Г. Петерсон, М.А. Кубышева, С.Е. Мазурина, И.В. Зайцева. – М.: УМЦ «Школа 2000…», 2008. – 80 с.
Литература 1. Александрова Э.И. Математика 1 класс / Э. И. Александрова – Учебник. В 2-х книгах. – М.: Вита-Пресс, 160 с. 2. Иванова Н.А., Бахтина О.В. Формирование мотивации к учебной деятельности у младших школьников / Н.А. Иванова, О.В. Бахтина. – Известия ВГПУ № 1 (270). – Воронеж, Изд-во ВГПУ, 2016. – С.21-25. 3. Кроссенс как инновационный приём обучения – URL: http://www. infourok.ru / (30.01.2016) 4. Маркова А.К. Формирование мотивации учения: книга для учителя / А.К. Маркова, А.Т. Матис, А.Б. Орлов. – М.: Просвещение, 1990. – 191 с. 5. Матюхина М.В. Мотивация учения у младших школьников / М.В. Матюхина. – М.: Педагогика, 1984. – 144 с. 6. Сухомлинский В.А. О воспитании / В.А. Сухомлинский. – Москва: Политическая литература, 1982. – 270 с. 7. Федеральный государственный образовательный стандарт начального общего образования – http://mon.gov.ru/files/materials/7195/373.pdf Вычислительных навыков У младших школьников Методика работы над каждым отдельным приёмом, указанном в предыдущем параграфе, предусматривает ряд этапов. Подготовка к введению нового приёма Центральное звено в процессе подготовки к новому приёму – овладение учеником основными операциями, составляющими его. Например, показателем готовности к введению приёма внетабличного умножения (14 · 5) будет знание правила умножения суммы на число, десятичного состава чисел, владение навыками табличного умножения, умножения числа 10 на однозначное число, сложения двузначных чисел. ФИО Уч-ся |
Правильность |
Рациональность | обобщён- ность | осознан- ность | прочность | |||||||||||||||||||||||||
| Выбрал операции верно | Вычислил верно | Вычислил одним способом | Вычислил разными способами | Подчеркнул | Выполнил верно | Назвал правило верно | Помнит все приемы | ||||||||||||||||||||||||
| 1. | + | – | + | + | – | + | – | – | |||||||||||||||||||||||
Успех проведения устного счёта заключается в его регулярном проведении. Начинать считать необходимо с первых уроков математики 1-го класса.
На современном этапе развития начального образования необходимо выбирать такие способы организации вычислительной деятельности младших школьников, которые способствуют не только формированию прочных осознанных вычислительных умений и навыков, но и всестороннему развитию личности ребёнка. Этого можно достичь, используя в процессе обучения устные упражнения, которые побуждают учащихся не только к воспроизведению результата, но и требуют наблюдения, анализа, сравнения.
В практике учителей начальных классов утвердилась добрая традиция: на каждом уроке специально отводить 5 – 7 минут для устных вычислений. Материал для этого этапа урока учитель подбирает из учебника, а также из сборников устных задач и упражнений. Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала. В зависимости от этого, учитель определяет место устного счёта на уроке. Если устные упражнения предназначаются для повторения ранее пройденного материала, формирования вычислительных навыков и готовят к изучению нового материала, то лучше их провести в начале урока до изучения нового материала. Если устные упражнения направлены на закрепление изученного материала на данном уроке, то необходимо провести устный счёт после изучения нового материала. Не следует устный счёт проводить в конце урока, так как дети уже утомлены, а устный счёт требует большого напряжения внимания, памяти, мышления. Количество упражнений должно быть таким, чтобы их выполнение не переутомляло детей и не превышало отведённого на это времени урока.
Задания для устного счёта предлагают младшим школьникам таким образом, чтобы они воспринимали их либо зрительно, либо на слух, либо зрительно и на слух.
В первом случае упражнения записываются на доске или оформляются на карточках, в таблице. Учащиеся зрительно воспринимают задание. Запись задания облегчает вычисление. Иногда без записи трудно и даже невозможно выполнить задание.
В отдельных случаях целесообразно предлагать задания для зрительного и слухового восприятия: кроме того, что упражнение читается учителем или учеником, оно записывается на доске или в тетради. При восприятии задания на слух учитель или один из учеников прочитывает его, а все остальные слушают. В этом случае большая нагрузка приходится на память, поэтому учащиеся быстро утомляются. Однако, такие упражнения очень полезны: они развивают слуховую память. Рекомендуется чередовать задания трёх видов. После того, как дети выполняют предложенное им задание, они поднимают руку и по указанию учителя несколько человек устно сообщают ответ. Можно предлагать детям показывать ответы с помощью разрезных цифр или на досках, это помогает включить в работу всех учеников, и, кроме того, учитель сразу увидит, как дети справились с заданием. Если ученик ошибся, ему предлагают выполнить вычисления вслух. Для обеспечения большей самостоятельности учащихся при выполнении устных упражнений, их предлагают по вариантам. Ученики записывают ответы в тетрадь, затем проверяют правильность вычислений, выясняют и исправляют ошибки.
В начальных классах рекомендуется как можно больше устных упражнений проводить в игровых формах. Такая форма заданий повышает интерес к математике. Выбирая игру, учитель должен руководствоваться тем, что только игра на уроке принесёт пользу, которая в короткое время даёт возможность вспомнить наибольшее число операций и охватить всех учащихся.
Математические цепочки.
Существует множество различных вариантов заданий для устного счета с помощью цепочек. Рассмотрим некоторые их них.
А) познавательные математические цепочки. Учащиеся, выполнив ряд арифметических действий, и соотнеся ответ с предложенными ответами, отвечают на один из познавательных вопросов.
Какое растение может заменить лампу?
| ? |
| 68 |
а) мох – 130
б) гриб – 126
в) герань – 142
Ответ: б) гриб – 126.
Можно добавить энциклопедические сведения: многие растения, особенно грибы, светятся по ночам. Некоторые создают столько света, что при нем можно читать. Некоторые виды герани, ноготков, мхов тоже светятся по ночам, но не так ярко, как грибы.
Б) математическая цепочка «Угадай задуманное число». Для поиска задуманного числа учащимся необходимо выполнять обратные действия и в обратном порядке
| 2 |
| ? |
Ответ: 990.
В) «Найди первое и последнее числа математической цепочки»
| 150 |
| ? |
| ? |
Ответ: первое число – 180
последнее число – 19
Г) «Двойная познавательная математическая цепочка»
И чего состоят метеориты?
а) из металла – 180
б) из камня - 480
| 150 |
| ? |
| 80 |
| 150 |
| ? |
Ответ: оба утверждения верны.
Можно добавить энциклопедические сведения: метеориты представляют собой обломки комет. Среди метеоритов можно выделить два основных вида. Относящиеся к первому виду состоят, главным образом, из железа и никеля. Они называются «металлическими» метеоритами. В состав других входят преимущественно различные минералы, и они выглядят как обожженные каменные глыбы.
Д) познавательная математическая цепочка. Учащие, ориентируясь на контуры стрелок, должны вставить в пустые квадраты соответствующие числовые значения и выполнить арифметические действия.
Какой континент самый жаркий, малонаселённый, удивительно богатый и разнообразный уникальными представителями флоры и фауны?
Евразия – 3 Африка – 4 Австралия – 5
Антарктида – 6 Северная Америка – 7 Южная Америка – 8
| ? |
| 9 |
-5 -6 -5 +9 +3
Ответ: Австралия
6. Примеры с окошками. Учащимся необходимо восстановить примеры, вставив вместо звёздочек соответствующие числа. Например:
(** – 30) + 30 = 60 (14 – 9) + * = 14
48 – (**– 48) = 48 (** + 26) – 26 = 13
Ответ: (60 – 30) + 30 = 60; 48 – (48 – 48) = 48; (14 – 9) + 9 = 14;
(13 + 26) – 26 = 13
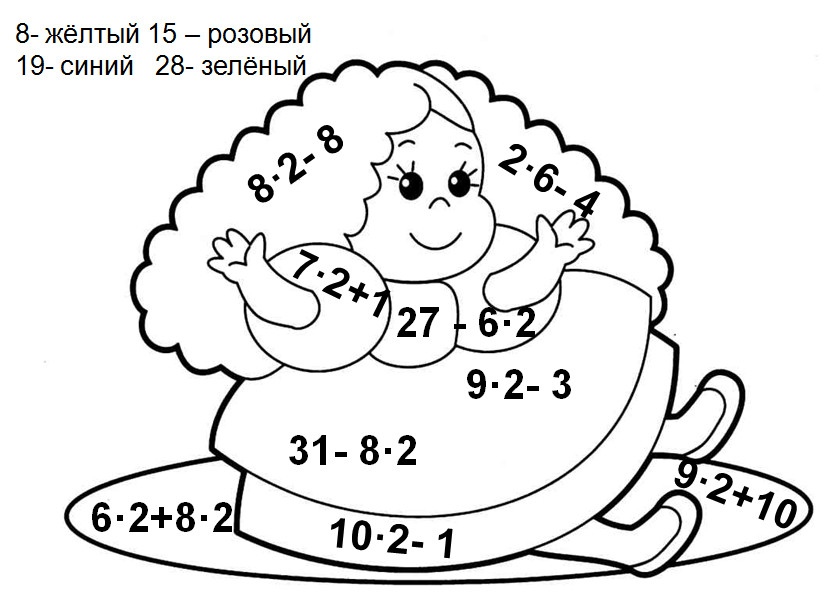
7. Задания для устного счета с элементами занимательности. А)Учащимся предлагается не только найти значения выражений, но и раскрасить рисунок соответствующими цветами. Например:
Б) Интересны задания для устного счета, предложенные И.И. Аргинской. Рассмотрим некоторые примеры:
Задание 1.Находи по порядку значения выражений и соединяй точки с соответствующими числами.
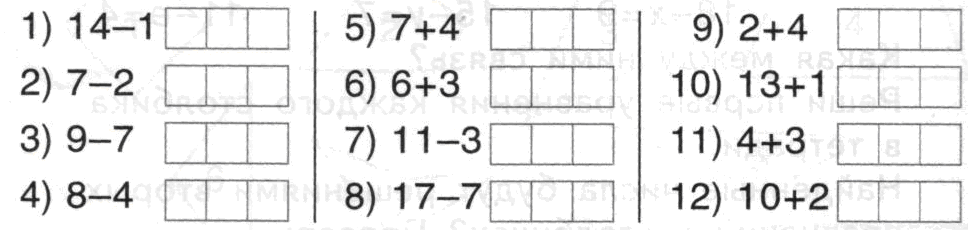

Подумай, где лучше соединять точки отрезками, а где – кривыми. Исправь рисунок.
При проверке вычислительных навыков можно параллельно предлагать задания и на усвоение нумерации. Например:
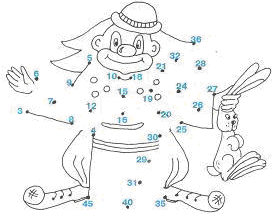
Задание 2. Сначала соедини в порядке возрастания все точки с числами, которые могут получиться при умножении однозначного числа на 5, затем – на 4, затем – на 3.
8. Задания для устного счета, содержащие элементы самостоятельности.
Задание: В лесной школе Белка, Заяц и Лисёнок написали по два выражения. Значения выражений Белки больше, чем Зайца. А значения выражений Лисёнка меньше, чем Зайца. Какие выражения они могли записать? Напиши выражения и их значения в тетрадках зверят.

Комплексные упражнения
И.И. Аргинская и Е.И. Ивановская для устного счета предлагают комплексные упражнения.
Например:
1) Как бы ты нашел значения произведений: 20 х 4, 30 х 2, 30 х 3?
2) При выполнении задания Вася, Света и Рома предложили такие способы:
Вася: 20 х 4 = (10 х 2) х 4 = 10 х (2 х 4) – 10 х 8 = 80
Света: 2 х 4 = 8, значит, если 2 десятка умножить на 4, получится 8 десятков. 20 х 4 = 80.
Рома: 20 х 4 = (10 + 10) х 4 = 10 х 4 + 10 х 4 = 40 + 40 = 80.
Как рассуждал каждый?
3) Какой способ тебе нравится больше? Объясни свой выбор.
4) Нам кажется самым лучшим способ Светы. Как ты думаешь, почему?
5) Если ты не знаешь, попробуй найти разными способами значения произведений: 60 х 7, 30 х 9, 80 х 5, 50 х 5.
6) Верно ли утверждение: его преимущество в том, что используется таблица умножения?
7) Найди этим способом значения произведений:
200 х 4 300 х 2 300 х 3 400 х 2 200 х 2 200 х 3
Сколько равенств из таблицы умножения понадобилось при решении? Почему их меньше, чем произведений?
или другой пример:
1) Найди значения частных:
372: 6 674: 2 840: 6 128: 4 170: 5 304: 2
2) Раздели получившиеся равенства на 2 группы так, чтобы в каждой группе они были похожи.
3) Дополни каждую группу несколькими подходящими к ней равенствами.
4) К каждому равенству запиши другие с теми же числами.
5) Предложи свое задание к данным в пункте 1 частным
10. «Игровые задания»
А) Игра «Магический квадрат».
Рамки занимательные
Очень увлекательные.
Тот, кто любит устный счет,
Быстро числа подберет!
Учащимся предлагается поле с числами. Необходимо вставить в пустые клетки числа таким образом, чтобы по горизонтали, вертикали и по диагонали сумма чисел была равна одному конкретному числу. Например:
| 2 | 6 | |
| 5 | ||
Сумма чисел по горизонтали, вертикали и диагонали равна 15.
Ответ:
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
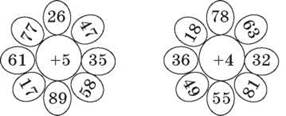
Б) Игра «Молчанка» («Ромашка»). Учащиеся, пользуясь веером цифр, молча показывают значение выражений, предложенных учителем.
11. Примеры с зашифрованным словом.
Учащимся предлагается найти значения выражений и соотнести их с соответствующими буквами, в результате чего получится зашифрованное то или иное слово. Например:
Узнайте имя сказочного героя. Назовите сказку и его автора
| 31 | 42 | 51 | 62 | 71 | 82 | 91 |
З – 1 + 19 Л – 37 +14 К – 39 + 43
О – 15 + 27 У – 49 + 13 А – 49 + 42
Ш – 35 + 36
Ответ: сказка «Золушка», автор Ш. Перро
- Что интересного заметили в ответах? Кто сможет продолжить закономерность?
Ответ: 91, 102, 111, 122, 131, 142
12. Зашифрованные примеры. Учащимся предлагаются примеры, записанные с помощью различных геометрических фигур. Необходимо заменить геометрические фигуры соответствующими числами таким образом, чтобы равенство было верным. Например:
+ + + + + =37
Ответ: 9+9+7+7+5=37
или другой пример: замените и такими числами, чтобы получились верные равенства:
+ = 77
+ = 77
+ =77
Ответ: 16 + 61 = 77; 52 + 25 = 77; 34 + 43 = 77
13. Круговые примеры. Учащимся предлагаются примеры, ответ первого примера является первым компонентом следующего примера и т.д., а результат последнего примера будет первым компонентом первого. Например: найдите значения выражений и подумайте, можно ли данные примеры назвать «круговыми»:
180: 20; 90 * 30; 270 – 120; 150: 3; 50 + 26; 76 + 104
Задания для устного счета, где необходимо восстановить знаки арифметических действий
А) Вставьте в пустые квадратики знаки «+» или «-»
6— 1 — 3 = 4 4 — 1 — 2 = 7
9 — 5 — 2 = 2 7 — 2 — 4 = 1
7 — 4 — 3 = 0 7 — 2 — 8 = 1
Б) Поставь пропущенные знаки «+» и «-»
а) ... =
б) *****...** = ***
в) ... =
В) Расставьте знаки действия и скобки между числами таким образом, чтобы равенство было верным:
40 * 1 * 2 * 3 * 4 * 5 = 40
Варианты решений: 40:1+2– (3+4)+5=40; 40:1:2*3–4*5=40
Г) Расставь знаки действий таким образом, чтобы получилось верное равенство
1) (75 * 6)* 9 = 9
2) 7 * 8 * 40 = 16
3) (80 * 38) * 7 = 6
4) 8 * 9 * 28 = 100
Ответы: 1) +: 2) × – 3) –: 4) × +
Д) Не меняя числовой последовательности от 1 до 9, необходимо вставить между числами знаки «+» и «–» таким образом, чтобы в результате получилось 100.
Варианты решения: 123 – 45 – 67 + 89 = 100
или другой пример:
Как при помощи восьми 8 и одного знака арифметического действия получить 1000?
Ответ: 888+88+8+8+8 = 1000
По нашему мнению, вычислительный навык можно считать эффективным, если в рамках данного способа вычислений получение правильного результата достигается минимизацией затрат умственных ресурсов. Т.е. ученик, используя различные знания, может выбрать не обязательно более рациональный вычислительный прием с точки зрения методики, а более удобный (легкий) для него в конкретной ситуации, быстрее других приводящий к результату.
III. Решение уравнений.
В качестве устных упражнений могут предлагаться и различные уравнения, как самые простейшие: х + 3 = 10, так и более сложные: (у + 5) – 7 = 23 и т.п.
Назначение данных упражнений – выработать умение решать уравнения, помочь учащимся усвоить связи между компонентами и результатами арифметических действий, а также способствовать выработке вычислительных навыков.
Например: Проведи путь через лабиринт только через уравнения, корни которых делятся на 5.
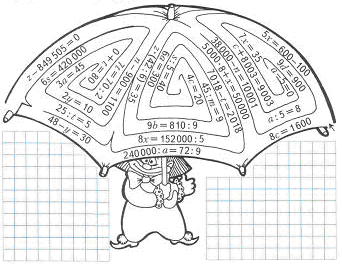
IV. Решение задач.
Для устной работы предлагаются задачи, как простые, так и составные. Эти упражнения помогают освоить теоретические знания и выработать вычислительные навыки. Необходимо предлагать детям различные упражнения для устных вычислений. Разнообразие заданий поддерживает интерес у детей, активизирует их мыслительную деятельность.
Простые задачи для устного счета могут быть сформулированы как в стихотворной форме, так и в прозаической. Приведем пример простой задачи, сформулированной в стихотворной форме:
«На траве во дворе
Бегают щенята
Двое белых, будто снег,
Трое черных. Сколько всех?»
Приведем пример составной задачи, сформулированной в прозаической форме: «Четыре альбома для рисования стоят 80 рублей. Сколько стоят 6 таких альбомов?»
Интерес к математике в младших классах поддерживается занимательностью самих задач, вопросов, заданий. Говоря о занимательности, надо иметь в виду не развлечение детей пустыми забавами, а занимательностью содержанием математических заданий. Педагогически оправданная занимательность имеет целью привлечь внимание детей, усилить его, активизировать их мыслительную деятельность.
Использование на уроках нестандартных приемов в формировании вычислительных навыков всегда несет элементы остроумия, игрового настроя, праздничности и даже юмора. Все это служит основой для проникновения в сознание ребят чувства прекрасного в самой математике.
Можно использовать некоторые из нестандартных приемов устных вычислений. Приведем пример:
Умножение двузначного числа на 11
(между цифрами первого множителя вписываем сумму этих чисел)
Например:
32 · 11 = 352
45 · 11 = 495
78 · 11 = 858
Прокомментируем последний пример: находим сумму чисел 7 и 8 (15). Количество единиц (5) вписываем между цифрами 7 и 8, а 1 десяток прибавляем к 7 десяткам.
Умножение трехзначного числа на 101.
Например: 125 · 101 = 12625
Увеличиваем первый множитель на число его сотен и приписываем к нему справа две последние цифры первого множителя.
125 + 1 = 126; 12625
Как легко умножить любое чётное двузначное число на 15?
Например: 14 · 15
Надо к первому множителю прибавить его половину и умножить результат на 10: 14 + 7 = 21, 21 · 10 = 210
56 · 15 1) 56 + 28 = 84, 2) 84 · 10 = 840
74 · 15 1) 74 + 37 = 111, 2) 111 · 10 = 1110
Следует подчеркнуть, что это правило справедливо только для чётных чисел.
Если же надо умножить нечётное число, то пользуются уже известным приёмом.
| 23 · 15: | Берём 22 · 15; | 22 + 11 = 33; | 33 · 10 = 330; | 330 + 15 = 345 | |
| 39 · 15: | Берём 38 · 15; | 38 + 19 = 57; | 57·10=570; 570+15= 585 | ||
Совершенствование навыков устных вычислений зависит не только от методики организации занятий, от форм, контроля, но и во многом от того насколько сами дети проявляют интерес к этой форме работы.
Таким образом, при выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающий характер работы, отдавать предпочтение обучающим заданиям, в которых познавательная мотивация выступает на первый план. Используемые вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением разнообразных закономерностей и зависимостей, использованием различных моделей (предметных, графических, символических), что позволяет учитывать индивидуальные особенности ребёнка, его жизненный опыт, предметно-действенное и наглядно-образное мышление и постепенно водить ребёнка в мир математических понятий, терминов и символов.
Вопросы и задания для самостоятельной работы
1. Раскройте содержание понятия «вычислительный навык» и охарактеризуйте все его качества.
2. Разработайте задания для индивидуальной карточки диагностики и профилактики ошибок в вычислениях по теме: «Вычитание в пределах 20».
3. Сформулируйте задания математического диктанта для учащихся 3-го класса.
4. Предложите задания для устного счета, используя коллективную форму работы. Прокомментируйте, как Вы организуете проверку результатов вычислений в группах?
5. Какие методические рекомендации Вы бы могли предложить по организации устного счета на уроках математики в начальной школе?
6. Какие виды упражнений для устного счета Вы используете наиболее часто в своей работе? Аргументируйте свой ответ.
Литература
1. Афоризмы. Высказывания великих о математике. – http://www.fizmat.lenlic.edusite.ru/p15aa1.html
2. Бенесон Е.П., Итина Л.С. Математика. – Рабочие тетради по математике для 1, 2,3,4 классов / Е.П. Бененсон, Л.С. Итина. – Самара: Федоров, 2014. – 64 с.
3. Зайцева С.
|
| Поделиться: |




