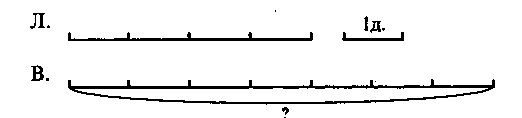Вещественные графические на естественном на математическом

                                           языке                  языке»

Все многообразие моделей можно представить в виде двух видов моделей: схематизированных и зна­ковых.

«Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они сопровождают. Вещественные (или предметные) модели текстовых задач обеспечивают физическое действие с предметами. Они могут сопровождаться какими-либо предме­тами (пуговицами, спичками, бумажными полосками и т.д.), могут быть представлены с помощью разного рода инсценировок сюжета задач. К этому виду моделей причисляют и мысленное вос­создание реальной ситуации, описанной в задаче, в виде представлений».

«Графические модели используются, как правило, для обобщённого, схематического воссоздания ситуации за­дачи. К графическим моделям следует отнести следующие виды моделей:

1) рисунок;

2) условный рисунок;

3) чертёж;

4) схематичный чертёж (или просто схема)».

Приведём примеры использования перечисленных моделей на примере конкретной текстовой задачи: «Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовал Вова?»

Рисунок в качестве графической модели этой задачи может иметь следующий вид:

 

Условный рисунок может выглядеть следующим образом:

Л.

 

В.

 

Чертёж как графическая модель должен быть выполнен при помощи чертёжных инструментов и с соблюдением заданных отношений:

 Схематический чертёж (схема) может быть выполнен следующим образом:

 

                   4 д.

Л.

                                            3 д.

В.

                                 ?      

«Знаковые модели могут быть выполнены как на естествен­ном языке, так и на математическом языке. К знаковым моде­лям, выполненным на естественном языке, можно отнести краткую запись задачи, таблицы».

Л. – 4 д.

В. –?, на 3 д. больше, чем

Таблица как вид знаковой модели используется главным образом тогда, когда в задаче имеется несколько взаимосвя­занных величин, каждая из которых задана одним или не­сколькими значениями.

Например, можно воспользоваться таблицей при анализе следующей текстовой задачи: «Два грузовика перевозили 77 тонн груза, сделав одинаковое число рейсов. Сколько тонн груза перевёз каждый грузовик, если один грузовик перевозил за рейс 3 т, а другой – 4 т?»

Рейсы	Тонн в 1 рейс	Количество рейсов	Всего тонн
I   II	3 т     4 т	? одинак. ?	? т             77 т  ? т

 

Знаковыми моделями текстовых задач, выполненными на математическом языке, являются: выражение, уравнение, система уравнений, запись решения задачи по действиям. Поскольку на этих моделях происходит решение задачи, их называют решающими моделями. Остальные модели, все схе­матизированные и знаковые, выполненные на естественном языке, - это вспомогательные модели, которые обеспечивают переход от текста задачи к математической модели.

Для большинства текстовых задач приходится строить различные вспомогательные модели. С одной стороны, эти модели представляют собой результат анализа задачи, но с другой - построение таких моделей организует и направляет детальный и глубокий анализ задачи.

Для эффективного обучения моделированию необходимо соблюдать следующие условия: 1) все математические понятия, используемые при решении задач, должны изучаться с помощью моделей; 2) должна проводиться работа по усвоению знаково-символического языка, на котором строится модель (при этом ученик должен осознавать значение каждого элемента модели, осуществляя переход от реальности (предметной модели) к модели, и наоборот); 3) необходимый этап обучения - освоение моделей тех отношений, которые рассматриваются в задачах, т.е. осознание сути отношения, которое раскрывается в задаче; 4) чтобы самостоятельно решать задачи, ученик должен освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче, и переходить от одной модели к другой.

Для овладения умением моделировать возможно использование следующих методических приёмов (могут использоваться для всех видов моделей): а) воспроизведение текста задачи по модели; б) составление задачи по модели; в) выбор среди предложенных моделей той, что соответствует данной задаче; г) выбор среди предложенных задач той, что соответствует данной модели; д) анализ уже построенной модели; е) изменение модели в соответствии с требованием; ж) запись решения по модели; з) выстраивание модели по решению; и) выбор решения, соответствующего модели; к) нахождение ошибок в предложенной модели; л) определение по модели всех арифметических способов решения данной задачи.

Таким образом, моделирование при решении текстовых задач может использоваться как приём алгоритмизации учебной деятельности учащихся, а изображение моделей может использоваться как внешние опоры организации мыслительной деятельности.