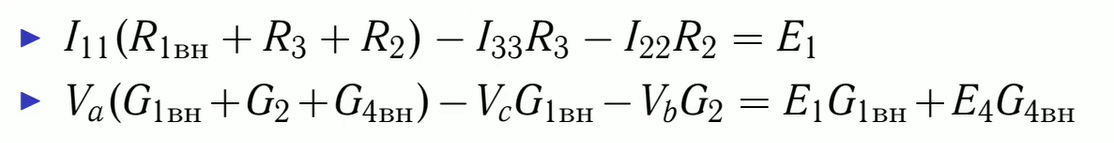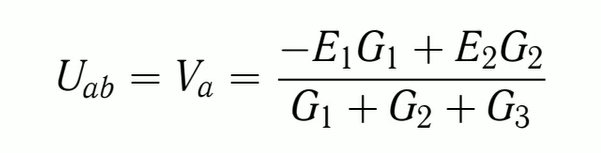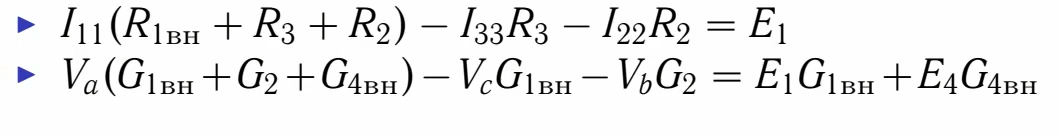Составляем уравнения по первому и второму закону Кирхгофа.

В итоге получаем систему уравнений:

ВАЖНОЕ!

 

Часть 3

Метод контурных токов

Идея метода:

Метод контурных токов основан на втором законе Кирхгофа и двух положениях:

1. В каждом контуре электрической цепи протекают независимые, расчётные токи, называемые контурными

2. Токи в ветвях цепи равны алгебраической сумме контурных токов, замыкающихся через эти ветви.

 

Порядок расчёта

1. Выделить в цепи независимые контуры (т.е. отличающиеся друг от друга хотя бы одной ветвью).

2. Составить уравнения по второму закону Кирхгофа, где токи в ветвях представляются в виде алгебраической суммы контурных токов, замыкающихся через рассматриваемую ветвь.

3. Решить полученную систему относительно неизвестных контурных токов удобным методом.

4. Определить искомые значения токов в ветвях как алгебраическую сумму контурных токов, замыкающихся через данную ветвь.

 

Метод узловых потенциалов

Идея метода:

Метод узловых потенциалов основан на первом законе Кирхгофа и двух положениях:

1. Токи в уравнениях по первому закону Кирхгофа выражаются по закону Ома.

2. Напряжения в выражениях по закону Ома представляются как разность потенциалов узлов, между которыми расположена соответствующая ветвь.

 

Порядок расчёта

1. Выбрать узел с нулевым потенциалом.

2. Для остальных узлов схемы составить уравнения по первому закону Кирхгофа, выразив токи через потенциалы узлов по закону Ома.

3. Решить полученную систему относительно неизвестных потенциалов удобным методом.

4. Определить искомые значения токов в ветвях по закону Ома

Метод двух узлов

 

Особенности метода двух узлов:

Метод двух узлов является частным случаем метода узловых потенциалов и применяется для цепей, имеющих два узла и неограниченное количество ветвей. В этом случае система линейных уравнений по первому закону Кирхгофа вырождается в одно уравнение.

 

Идея метода:

На основе выражения по методу узловых потенциалов находится напряжение между узлами. Затем вычисляются токи в ветвях по закону Ома.

 

Важное:

Выражения для уравнений по методам контурных

токов и узловых потенциалов:

Токи в ветвях находятся:

> как алгебраическая сумма контурных токов

> по закону Ома

Для цепи имеющей два узла и большое количество параллельных ветвей удобно воспользоваться методом двух узлов:

 

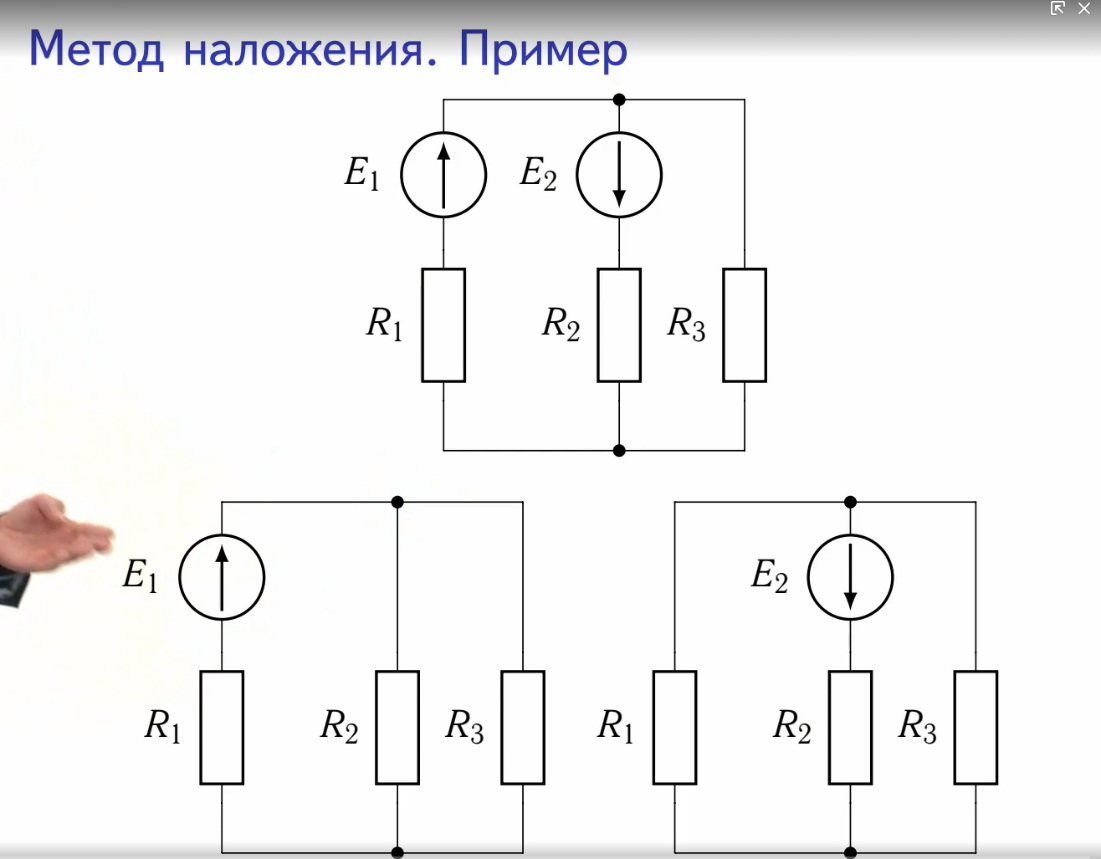
Лекция 2 Часть 4

Цепи постоянного тока.

Методы расчета электрических цепей.

-------------------------------------------------------

Методы наложения и эквивалентного генератора (активного двухполюсника).

Метод наложения.

Принцип суперпозиции.

Результат воздействия нескольких внешних сил есть Векторная сумма воздействия этих сил.

Принцип наложения (суперпозиции) является одним из самых общих законов физики и является прямым следствием свойств линейных уравнений.

Идея метода.

Ток в любой ветви электрической цепи равен алгебраической сумме токов, вызываемых каждым из действующих в цепи источников в отдельности.

Порядок расчета.

1.В имеющейся цепи выделить вспомогательные схемы, каждая из которых содержит один из имеющихся в цепи источников электрической энергии.

2.Провести расчет токов во вспомогательных схемах любым известным методом.

3.Найти токи в ветвях как алгебраическую сумму токов в соответствующих ветвях вспомогательных схем.

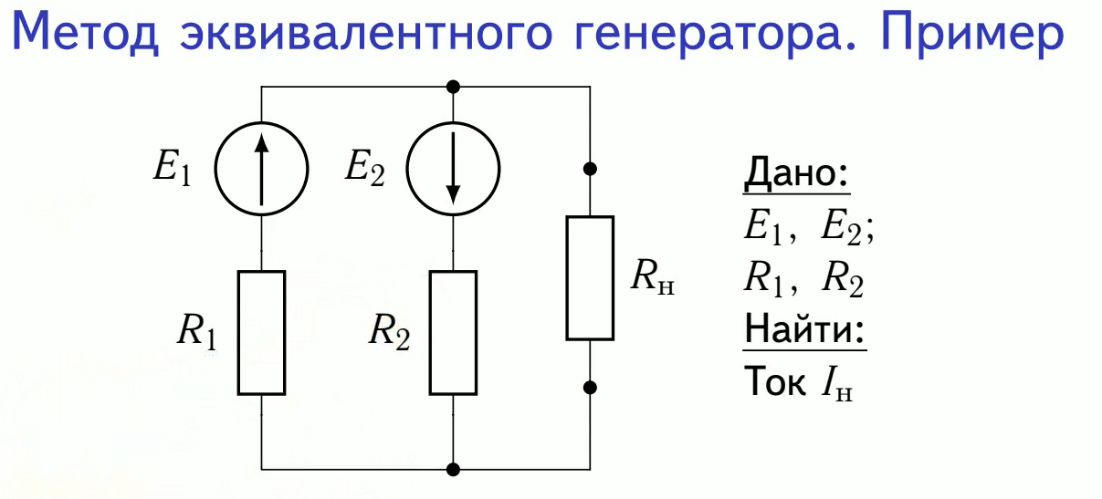
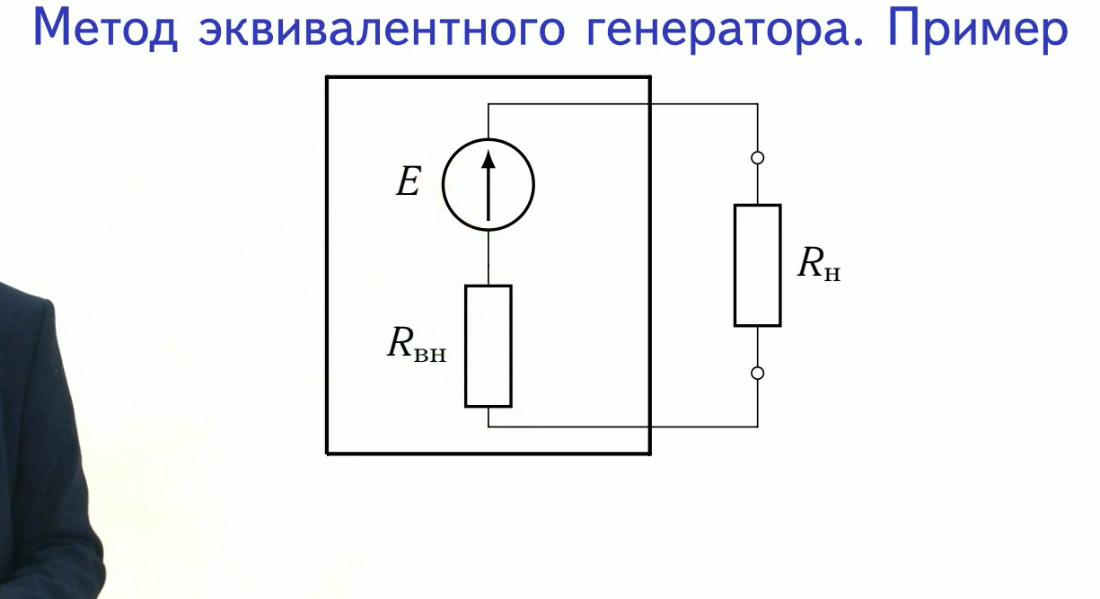
Метод эквивалентного генератора (активного двухполюсника).

Особенности метода:

 Метод экв.генератора (акт.двухполюсника) используется для определения тока в одной из ветвей сложно электрической цепи, без расчета всей цепи.

Эквивалентный генератор (активный двухполюсник):

Электрическая схема, имеющая два вывода и содержащая источник, электрической энергии.

Идея метода:

Состоит в замене участка электрической цепи, имеющего два вывода (двухполюсника) и содержащего активные и пассивные элементы, эквивалентным генераторов, ЭДС, которого равна напряжению холостого хода на выводах двухполюсника, а внутреннее сопротивление равно входному сопротивлению двухполюсника.

Порядок расчета:

1.Исключить из цепи ветвь, для которой выполняется расчет.

2.Оставшуюся цепь представить в виде эквивалентного генератора, рассчитав его ЭДС (E=Uxx) и внутреннее сопротивление (Rвн=Rвх).

3.Рассчитать искомый ток Iиск в заданной ветви по формуле Iиск = E/(Rвн + Rиск)

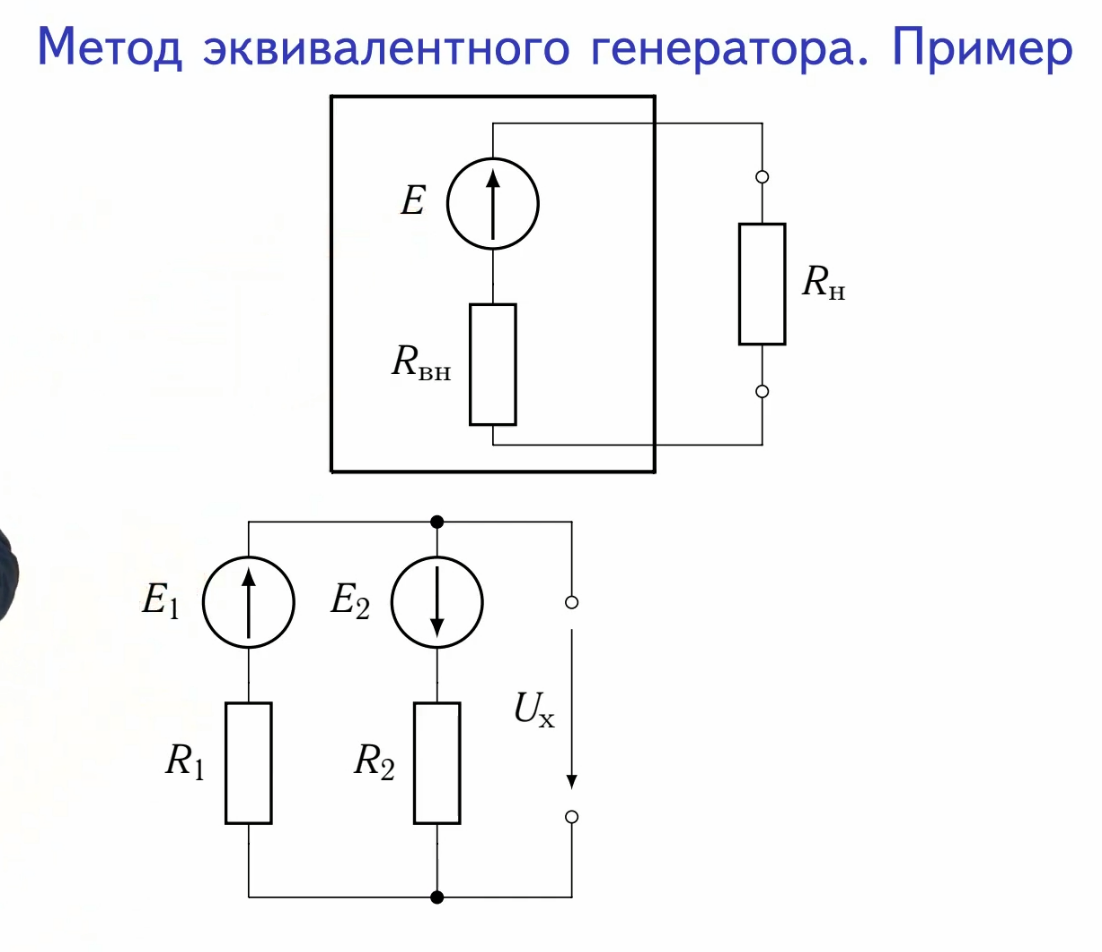
Представляем схему в виде эквивалентного генератора:

 

 

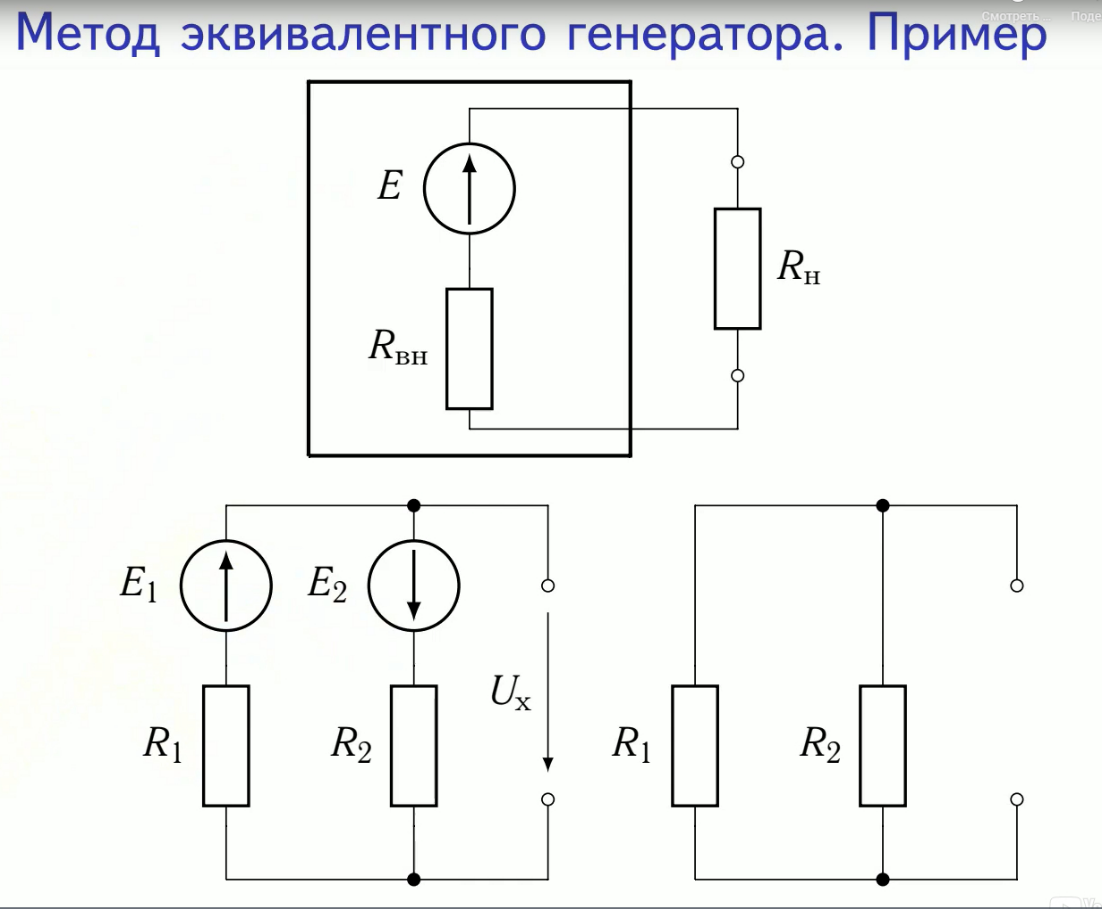
Чтобы найти напряжение холостого хода, нужно убрать нагрузочный элемент и найти напряжение между двумя выводами:

 

Что бы найти Rвх, мы удаляем все источники и методом эквивалентных преобразований рассчитываем:

По з-ну Ома находим ток во всей ветви (рис.сверху).

Важные вопросы Лекции 2:

1.В цепи постоянного тока Ul=0, Ic=0;

2.Баланс мощность: Сумма I^2R= Cумма IE;

3.Метод эквивалентных преобразований (применяйте знания что такое ветвь, узел, контур);

4.Метод применения законов Кирхгофа;

5.Метод контурных токов и узловых потенциалов;

6.Метод наложения.

7.Метод эквивалентного генератора (активного двухполюсника).

 

Лекция 4

1. Синусоидальный ток, основные характеризующие его величины

и соотношения.

2. Формула Эйлера и комплексная плоскость. Изображение синусоидальной функции времени в виде векторов на комплексной плоскости.

3. Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма.

4. Мгновенная мощность. Резистивный элемент, индуктивность и ёмкость в цепи синусоидального тока.

5. Символический метод. Комплексное сопротивление. Законы Кирхгофа в символической форме. Символический метод расчета. Векторные диаграммы. Законы Кирхгофа в символической форме. Применение МУП, МКТ и МЭГ.