
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Ома в комплексной форме, комплексное сопротивление. Законы Кирхгофа в символической форме. Символический метод расчета.
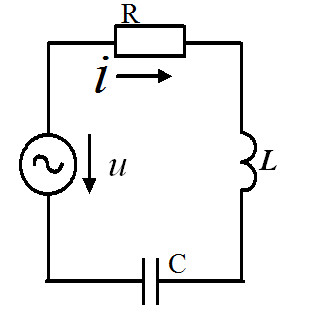
Рассмотрим цепь с последовательным соединением резистора, индуктивной катушки и конденсатора (рис.5.8). Для этой схемы уравнение по второму закону Кирхгофа имеет вид:
Рисунок 5.8 – Цепь с последовательным соединением резистора, индуктивной катушки и конденсатора Перепишем это уравнение в комплексной форме с учетом (2.53) и (2.54):
откуда:
где 0. Полученное выражение называется комплексное сопротивление цепи. Формулу (2.56) называют законом Ома в комплексной форме записи. Уравнение (2.54) является линейным дифференциальным уравнением второго порядка. Следовательно, нахождение тока, как функции времени сводится к решению этого дифференциального уравнения. Уравнение (2.55) является линейным алгебраическим уравнением с комплексными коэффициентами. Таким образом, символический метод позволяет перейти от решения дифференциальных уравнений к решению уравнений алгебраических, но с комплексными коэффициентами. В результате такого решения находится символическое изображение искомой величины (тока или напряжения), после чего осуществляют переход к мгновенным значениям. Для расчета цепей постоянного тока разработан ряд методов и приемов, позволяющих облегчить решение по сравнению с решением системы уравнений при непосредственном использовании законов Кирхгофа. К их числу относят метод контурных токов, метод узловых потенциалов и др. Окончательные расчетные формулы этих методов поучают в результате выводов, в основе которых лежат первый и второй законы Кирхгофа. Поскольку законы Кирхгофа справедливы и для цепей синусоидального тока, можно было бы записать уравнения для мгновенных значений величин цепей синусоидального тока, перейти от них к уравнениям в символической форме и затем воспользоваться методами расчета цепей постоянного тока. Методы пригодны и для цепей синусоидального тока, если вместо постоянного тока I подставить его символическое изображение Í, вместо проводимости g – комплексную проводимость Y, вместо сопротивления R – комплексное сопротивление Z и вместо постоянной ЭДС E – комплексную ЭДС É.
Лекция 3 часть 2
3.1 Резонансы в электрических цепях. 3.1.1 Резонанс напряжений.
3.1.2 Резонанс токов. 3.2 Частотные характеристики последовательного и параллельного резонансного контуров и реактивных двухполюсников. 3.4 Понятие добротности и полосы пропускания. 3.5 Линейный трансформатор. Вносимое сопротивление. Развязка индуктивных связей. Э
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением. Резонанс в цепи с последовательно соединенными элементами
Для цепи на рис.1 имеет место
где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е.
2.В цепи преобладает емкость, т.е. 3. Условие резонанса напряжений
При этом, как следует из (1) и (2), При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Пусть, например, в цепи на рис. 1 Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .
Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать
Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:
- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
или с учетом (4) и (5) для
Резонанс в цепи с параллельно соединенными элементами
Для цепи рис. 4 имеем
где
В зависимости от соотношения величин
В цепи преобладает индуктивность, т.е В цепи преобладает емкость, т.е.
Условие резонанса токов
При этом, как следует из (8) и (9), Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная частота определяется соотношением (4). Однако не следует использовать выражение (4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов. При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.
Например, для цепи на рис. 6 имеем
Поскольку в режиме резонанса мнимая часть
откуда, в частности, находится резонансная частота. Резонанс в сложной цепи (дополнительно) Условие резонанса для сложной цепи со смешанным соединением нескольких индуктивных и емкостных элементов, заключающееся в равенстве нулю мнимой части входного сопротивления При определении резонансных частот для реактивного двухполюсника аналитическое выражение его входного реактивного сопротивления
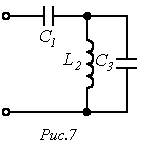
В качестве примера определим резонансные частоты для цепи рис. 7. Выражение входного сопротивления данной цепи имеет вид
Из решения уравнения
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.24 (0.02 с.) |






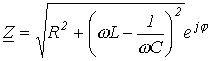 ;
;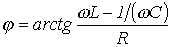 .
. и
и 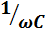 возможны три различных случая.
возможны три различных случая. , а следовательно,
, а следовательно, . Этому режиму соответствует векторная диаграмма на рис. 2,а.
. Этому режиму соответствует векторная диаграмма на рис. 2,а.
 , а значит,
, а значит, 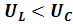 . Этот случай отражает векторная диаграмма на рис. 2,б.
. Этот случай отражает векторная диаграмма на рис. 2,б. - случай резонанса напряжений (рис. 2,в).
- случай резонанса напряжений (рис. 2,в). .
. .
.

 . Тогда
. Тогда  , и, соответственно,
, и, соответственно, 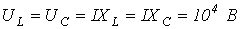 .
.
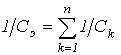 ,
,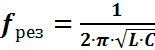 .
. и
и  для цепи на рис. 1 при U=const.
для цепи на рис. 1 при U=const. ,
, .
. ,
, можно записать:
можно записать: .
.

 ,
,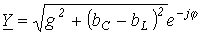 ;
;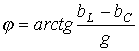 .
. , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
 , а следовательно,
, а следовательно,  . Этому режиму соответствует векторная диаграмма на рис. 5,а.
. Этому режиму соответствует векторная диаграмма на рис. 5,а. , а значит,
, а значит,  . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
. Этот случай иллюстрирует векторная диаграмма на рис. 5,б. - случай резонанса токов (рис. 5,в).
- случай резонанса токов (рис. 5,в).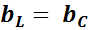 или
или .
. . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
. Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.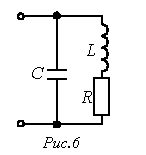
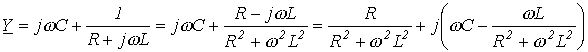
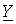 должна быть равна нулю, то условие резонанса имеет вид
должна быть равна нулю, то условие резонанса имеет вид ,
,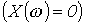 или входной проводимости
или входной проводимости  , определяет наличие у соответствующих этому условию уравнений относительно
, определяет наличие у соответствующих этому условию уравнений относительно 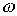 нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот.
нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот. или входной реактивной проводимости
или входной реактивной проводимости  следует представить в виде отношения двух полиномов по степеням
следует представить в виде отношения двух полиномов по степеням  или
или  . Тогда корни уравнения
. Тогда корни уравнения  дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения
дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения 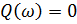 - значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
- значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
 получаем частоту
получаем частоту  , соответствующую резонансу напряжений, а из решения уравнения
, соответствующую резонансу напряжений, а из решения уравнения  - частоту
- частоту 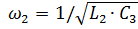 ,, соответствующую резонансу токов.
,, соответствующую резонансу токов.


